正弦定理
图片预览



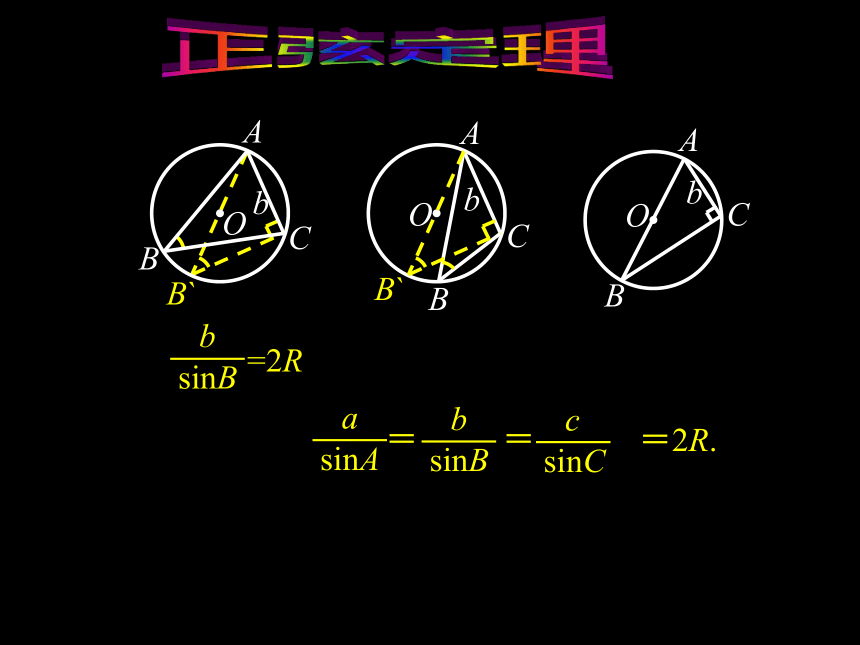

文档简介
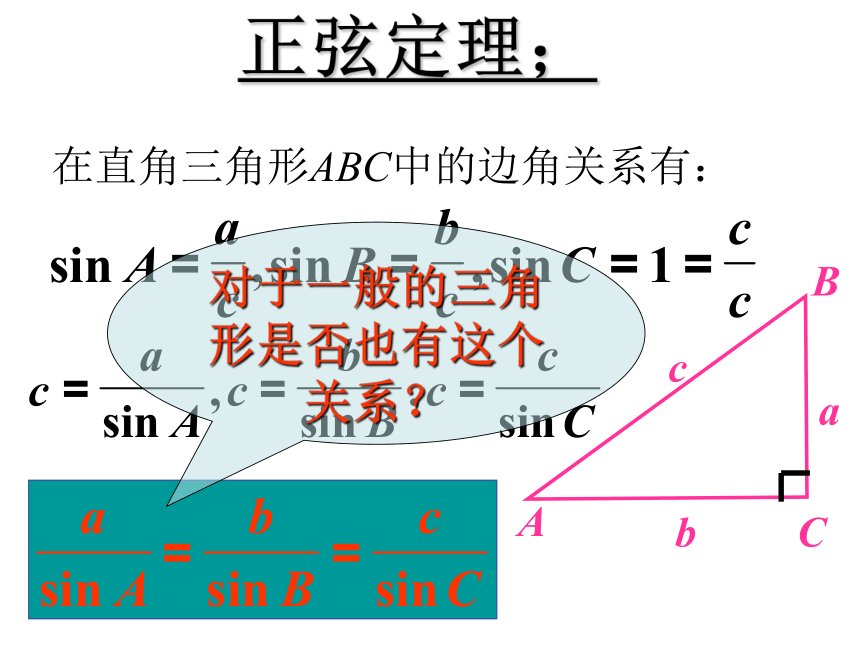
课件19张PPT。正弦定理正弦定理正弦定理;在直角三角形ABC中的边角关系有:对于一般的三角形是否也有这个关系?正弦定理证明一:在任意斜△ABC当中:
S△ABC=
两边同除以 即得: = =
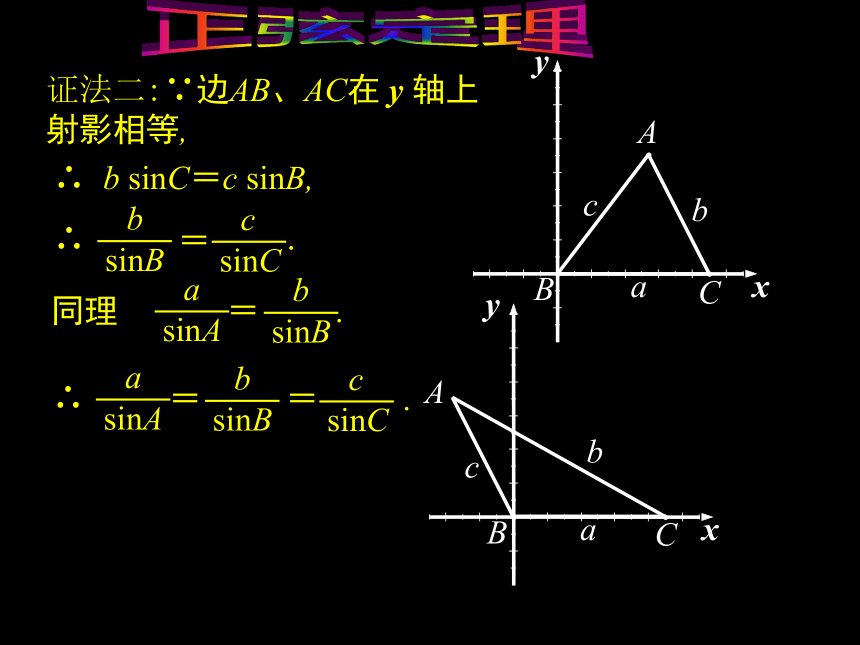
证法二:∵边AB、AC在 y 轴上 射影相等,∴ b sinC=c sinB,正弦定理 在一个三角形中各边和它所对角的正弦的比相等.=正弦定理?正弦定理正弦定理(1)已知两角及一边;(2)已知两边和其中一边的对角;(3)已知两边及夹角; (用余弦定理)(4)已知三边.(用余弦定理)正弦定理例 1 在?ABC中,已知c=10,A=45°,
C=30°,求b.解:B=180°– (A+C)=105°,正弦定理注:这是一类已知两角和任一边,求其他两边和一角问题例 2 在?ABC中,已知a=20,b=28,
A=40°,求B和c.解:∴ B1=64°,B2=116°40°ABCb······正弦定理注:这是一类已知两边的其中一边的对角解三角形的问题 在例 2 中,将已知条件改为以下几种情况,结果如何?(3) b=20,A=60°,a=15.正弦定理B=30°或150°,∵ 150°+60°> 180°,∴ B=150°应舍去.正弦定理B=90°.正弦定理(3) b=20,A=60°,a=15.∴ 无解. 思考: 当b=20,A=60°,a=?时,
有1解、2解、无解.正弦定理30°练习 ?ABC中,75°或15°正弦定理小结2. 正弦定理可解以下两种类型的三角形:
(1)已知两角及一边;(只有一解)
(2)已知两边及其中一边的对角→↓.正弦定理解三角形时,注意大边对大角正弦定理⑴若A为锐角时:⑵若A为直角或钝角时:正弦定理1、已知在 2、在 3、 作业:再见
S△ABC=
两边同除以 即得: = =
证法二:∵边AB、AC在 y 轴上 射影相等,∴ b sinC=c sinB,正弦定理 在一个三角形中各边和它所对角的正弦的比相等.=正弦定理?正弦定理正弦定理(1)已知两角及一边;(2)已知两边和其中一边的对角;(3)已知两边及夹角; (用余弦定理)(4)已知三边.(用余弦定理)正弦定理例 1 在?ABC中,已知c=10,A=45°,
C=30°,求b.解:B=180°– (A+C)=105°,正弦定理注:这是一类已知两角和任一边,求其他两边和一角问题例 2 在?ABC中,已知a=20,b=28,
A=40°,求B和c.解:∴ B1=64°,B2=116°40°ABCb······正弦定理注:这是一类已知两边的其中一边的对角解三角形的问题 在例 2 中,将已知条件改为以下几种情况,结果如何?(3) b=20,A=60°,a=15.正弦定理B=30°或150°,∵ 150°+60°> 180°,∴ B=150°应舍去.正弦定理B=90°.正弦定理(3) b=20,A=60°,a=15.∴ 无解. 思考: 当b=20,A=60°,a=?时,
有1解、2解、无解.正弦定理30°练习 ?ABC中,75°或15°正弦定理小结2. 正弦定理可解以下两种类型的三角形:
(1)已知两角及一边;(只有一解)
(2)已知两边及其中一边的对角→↓.正弦定理解三角形时,注意大边对大角正弦定理⑴若A为锐角时:⑵若A为直角或钝角时:正弦定理1、已知在 2、在 3、 作业:再见
