11.3.1多边形同步练习
图片预览


文档简介
11.3 多边形及其内角和
11.3.1 多边形
一、基 础 题 训 练
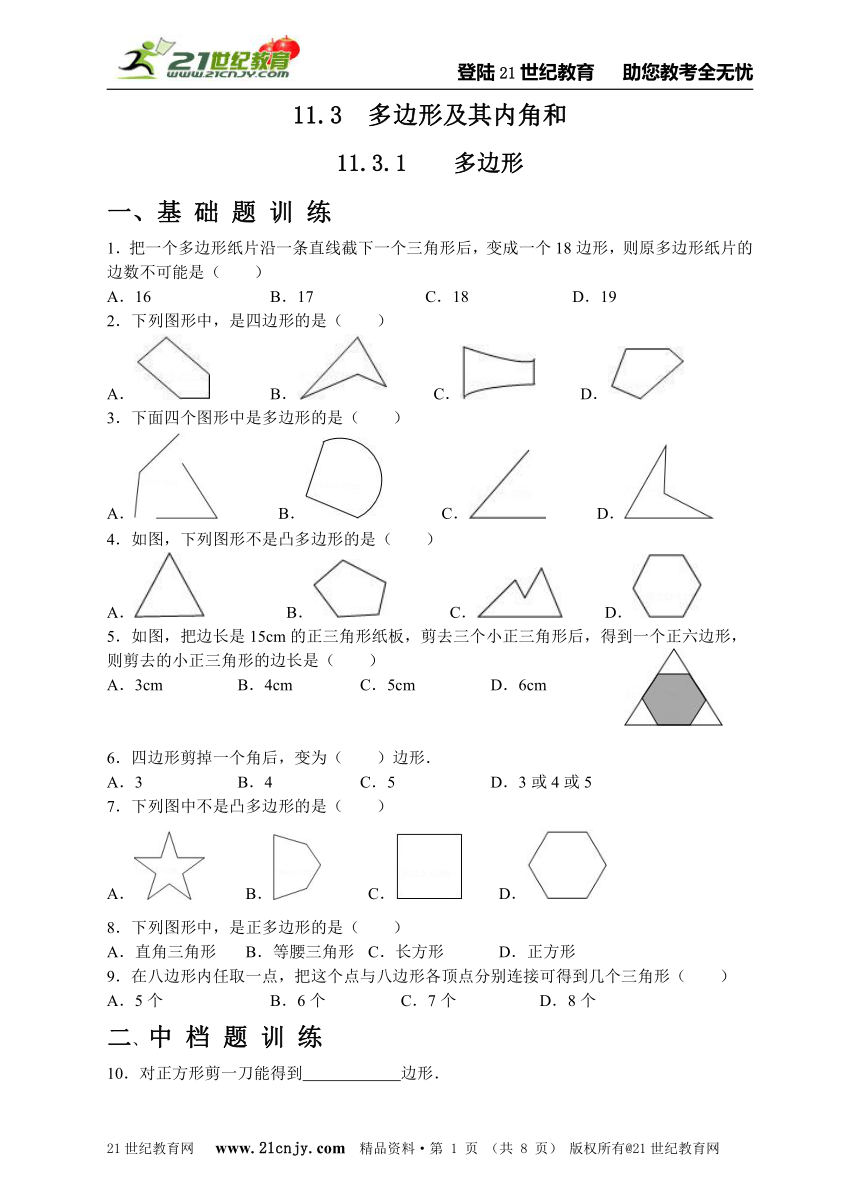
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )【版权所有:21教育】
A.16 B.17 C.18 D.19
2.下列图形中,是四边形的是( )
A. B. C. D.
3.下面四个图形中是多边形的是( )
A. B. C. D.
4.如图,下列图形不是凸多边形的是( )
A. B. C. D.
5.如图,把边长是15cm的正三角形纸板,剪去三个小正三角形后,得到一个正六边形,则剪去的小正三角形的边长是( )21·世纪*教育网
A.3cm B.4cm C.5cm D.6cm
6.四边形剪掉一个角后,变为( )边形.
A.3 B.4 C.5 D.3或4或5
7.下列图中不是凸多边形的是( )
A. B. C. D.
8.下列图形中,是正多边形的是( )
A.直角三角形 B.等腰三角形 C.长方形 D.正方形
9.在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形( )
A.5个 B.6个 C.7个 D.8个
二、中 档 题 训 练
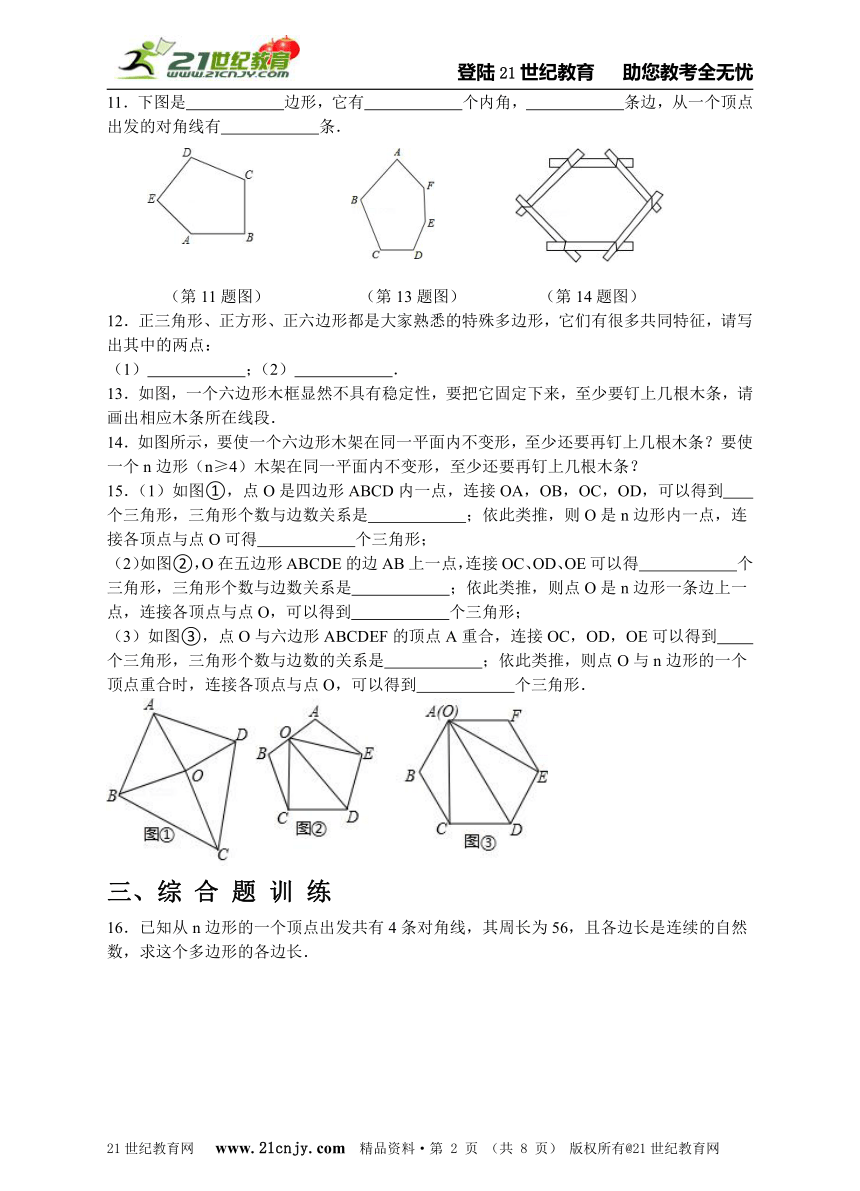
10.对正方形剪一刀能得到 边形.
11.下图是 边形,它有 个内角, 条边,从一个顶点出发的对角线有 条.21·cn·jy·com
(第11题图) (第13题图) (第14题图)
12.正三角形、正方形、正六边形都是大家熟悉的特殊多边形,它们有很多共同特征,请写出其中的两点:
(1) ;(2) .
13.如图,一个六边形木框显然不具有稳定性,要把它固定下来,至少要钉上几根木条,请画出相应木条所在线段.www.21-cn-jy.com
14.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
15.(1)如图①,点O是四边形ABCD内一点,连接OA,OB,OC,OD,可以得到 个三角形,三角形个数与边数关系是 ;依此类推,则O是n边形内一点,连接各顶点与点O可得 个三角形;www-2-1-cnjy-com
(2)如图②,O在五边形ABCDE的边AB上一点,连接OC、OD、OE可以得 个三角形,三角形个数与边数关系是 ;依此类推,则点O是n边形一条边上一点,连接各顶点与点O,可以得到 个三角形;
(3)如图③,点O与六边形ABCDEF的顶点A重合,连接OC,OD,OE可以得到 个三角形,三角形个数与边数的关系是 ;依此类推,则点O与n边形的一个顶点重合时,连接各顶点与点O,可以得到 个三角形.
三、综 合 题 训 练
16.已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边长.
17.如图,五边形ABCDE中,∠A=135°,延长CD,AE交于点F,且∠DEF=105°,∠F=45°,∠C=60°.
(1)求∠B的度数;
(2)AB与CD之间是否存在某种关系,说出你的理由.
参考答案与试题解析
点评:此题主要考查了多边形,剪去一个角的方法可能有三种:经过两个相邻顶点,则少了一条边;经过一个顶点和一边,边数不变;经过两条邻边,边数增加一条.
2.
考点:多边形.21世纪教育网
解析:根据四边形的定义,由四条线段首尾顺次连接而成的图形是四边形,再结合图形进行判断即可.A、D的图形都由5条线段组成,是五边形;2·1·c·n·j·y
C、围成图形的不都是线段,所以不是四边形;
只有B选项符合四边形的定义.
点评:理解四边形的定义,是解决本题的关键,此题属于简单题型.
3.
考点:多边形.
解析:根据多边形的定义:平面内不在一条直线上的线段首尾顺次相接组成的图形叫多边形.根据图形可知D是多边形.故选D.【来源:21·世纪·教育·网】
点评:理解多边形的概念,D中的多边形是一个凹多边形.
4.
考点:多边形.21世纪教育网
解析:根据凸多边形的定义进行判断.选项A、B、D中,画出这个多边形的任意一条边所在的直线,整个多边形都在这条直线的同一侧,所以都是凸多边形,只有C不符合凸多边形的定义,不是凸多边形.故选C.【出处:21教育名师】
点评:正确理解凸多边形的定义是解决此类问题的关键.
5.考点:等边三角形的性质.21世纪教育网
分析:由题意可知剪去的三个三角形是全等的等边三角形,可知得到剪去的小正三角的边长为5.
点评:本题主要考查等边三角形的性质,熟练掌握等边三角形的性质定理是解题的关键.
6.
考点:多边形.21世纪教育网
解答:解:如下图所示:
观察图形可知,四边形减掉一个角后,剩下的图形可能为五边形,可能为四边形,可能为三角形,
故选D.
点评:本题考查了多边形,解题的关键是能理解一个四边形减掉一个角后得到的图形的形状,通过画图的方法解决最好. 21*cnjy*com
7.考点:多边形.21世纪教育网
分析:根据凸多边形的概念,如果多边形的边都在任何一条边所在的直线的同旁,该多边形即是凸多边形.否则即是凹多边形.【来源:21cnj*y.co*m】
解答:解:选项B、C、D中,画出这个多边形的任意一条边所在的直线,整个多边形都在这条直线的同一侧,所以都是凸多边形,只有A不符合凸多边形的定义,不是凸多边形.
故选A.
点评:本题考查了多边形,正确理解凸多边形的定义是解决此类问题的关键.
8.
9.
考点:多边形.21世纪教育网
分析:根据八边形的顶点,连接点与顶点,可得答案.
解答:解:如图,故选:D.
点评:本题考查了多边形,画图是解题关键.
10.
考点:多边形.21世纪教育网
分析:根据图形的分割,可得答案.
点评:本题考查了多边形,分类讨论是解题关键.
11.
考点:多边形;多边形的对角线.21世纪教育网
分析:根据n边形的边、角、对角线,可得答案.
解答:解:是 五边形,它有五个内角,五条边,从一个顶点出发的对角线有2条,
故答案为:五,五,五,2.
点评:本题考查了多边形,n边形有n条边,n个内角,(n﹣3)条对角线.
12.
考点:多边形.21世纪教育网版权
分析:正多边形的特征是每条边都相等,每个内角都相等.
解答:解:正三角形、正方形、正六边形都属于正多边形,正多边形的特征是每条边都相等,每个内角都相等.
故答案为:(1)每条边都相等;(2)每个内角都相等.
点评:本题主要考查正多边形的性质.比较简单.
13.
考点:多边形;三角形的稳定性.21世纪教育网
点评:此题主要考查了三角形的稳定性,过n边形的一个顶点作对角线,可以做(n﹣3)条.
14.
考点:多边形;三角形的稳定性.
分析:从一个多边形的一个顶点出发,能做(n﹣3)条对角线,把三角形分成(n﹣2)个三角形.
15.
考点:多边形的对角线.21世纪教育网
分析:规律型.(1)根据图形可以得4个三角形,它与边数相等,则O是n边形内一点,连接各顶点与点O可得4个三角形;21世纪教育网版权所有
(2)根据图形可以得4个三角形,它的个数比边数小1,则点O是n边形一条边上一点,连接各顶点与点O,可以得到4个三角形;21教育网
(3)根据图形可以得到4个三角形,它的个数比边数小2,则点O与n边形的一个顶点重合时,连接各顶点与点O,可以得到4个三角形21cnjy.com
解答:解:(1)连接OA、OB、OC、OD可以得4个三角形,它与边数相等,则O是n边形内一点,连接各顶点与点O可得4个三角形;21教育名师原创作品
故答案为:4,相等,4;
(2)连接OC、OD、OE可以得4个三角形,它的个数比边数小1,则点O是n边形一条边上一点,连接各顶点与点O,可以得到4个三角形;21*cnjy*com
故答案为:4,个数比边数小1,4;
(3)过点A作六边形ABCDEF的对角线,可以得到4个三角形,它的个数比边数小2,则点O与n边形的一个顶点重合时,连接各顶点与点O,可以得到4个三角形.
故答案为:4,个数比边数小2,4.
点评:此题考查了多边形的对角线,关键是观察图形,找出三角形的个数与多边形的边数之间的关系.
16.
考点:多边形的对角线.21世纪教育网
分析:根据n边形从一个顶点出发可引出(n﹣3)条对角线,可求多边形的边数,再根据多边形的周长的定义可求这个多边形的各边长.
点评:考查了多边形的对角线,熟悉从多边形的一个顶点出发的对角线条数公式是解题关键.
17.
考点:多边形内角与外角;平行线的判定.菁优
分析:(1)首先求得∠DEA和∠EDC的度数,然后利用多边形的内角和定理可求得∠B的度数;
(2)根据∠B+∠C=180°可判定AB∥CD.
解答:证明:(1)∵∠DEF=105°,
(2)∵∠B=120°,∠C=60°,
∴∠B+∠C=180°.
∴AB∥CD.
点评:本题主要考查的是三角形的外角的性质、多边形的内角和公式、平行线的判定,求得∠DEA和∠EDC的度数是解题的关键.2-1-c-n-j-y
11.3.1 多边形
一、基 础 题 训 练
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )【版权所有:21教育】
A.16 B.17 C.18 D.19
2.下列图形中,是四边形的是( )
A. B. C. D.
3.下面四个图形中是多边形的是( )
A. B. C. D.
4.如图,下列图形不是凸多边形的是( )
A. B. C. D.
5.如图,把边长是15cm的正三角形纸板,剪去三个小正三角形后,得到一个正六边形,则剪去的小正三角形的边长是( )21·世纪*教育网
A.3cm B.4cm C.5cm D.6cm
6.四边形剪掉一个角后,变为( )边形.
A.3 B.4 C.5 D.3或4或5
7.下列图中不是凸多边形的是( )
A. B. C. D.
8.下列图形中,是正多边形的是( )
A.直角三角形 B.等腰三角形 C.长方形 D.正方形
9.在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形( )
A.5个 B.6个 C.7个 D.8个
二、中 档 题 训 练
10.对正方形剪一刀能得到 边形.
11.下图是 边形,它有 个内角, 条边,从一个顶点出发的对角线有 条.21·cn·jy·com
(第11题图) (第13题图) (第14题图)
12.正三角形、正方形、正六边形都是大家熟悉的特殊多边形,它们有很多共同特征,请写出其中的两点:
(1) ;(2) .
13.如图,一个六边形木框显然不具有稳定性,要把它固定下来,至少要钉上几根木条,请画出相应木条所在线段.www.21-cn-jy.com
14.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
15.(1)如图①,点O是四边形ABCD内一点,连接OA,OB,OC,OD,可以得到 个三角形,三角形个数与边数关系是 ;依此类推,则O是n边形内一点,连接各顶点与点O可得 个三角形;www-2-1-cnjy-com
(2)如图②,O在五边形ABCDE的边AB上一点,连接OC、OD、OE可以得 个三角形,三角形个数与边数关系是 ;依此类推,则点O是n边形一条边上一点,连接各顶点与点O,可以得到 个三角形;
(3)如图③,点O与六边形ABCDEF的顶点A重合,连接OC,OD,OE可以得到 个三角形,三角形个数与边数的关系是 ;依此类推,则点O与n边形的一个顶点重合时,连接各顶点与点O,可以得到 个三角形.
三、综 合 题 训 练
16.已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边长.
17.如图,五边形ABCDE中,∠A=135°,延长CD,AE交于点F,且∠DEF=105°,∠F=45°,∠C=60°.
(1)求∠B的度数;
(2)AB与CD之间是否存在某种关系,说出你的理由.
参考答案与试题解析
点评:此题主要考查了多边形,剪去一个角的方法可能有三种:经过两个相邻顶点,则少了一条边;经过一个顶点和一边,边数不变;经过两条邻边,边数增加一条.
2.
考点:多边形.21世纪教育网
解析:根据四边形的定义,由四条线段首尾顺次连接而成的图形是四边形,再结合图形进行判断即可.A、D的图形都由5条线段组成,是五边形;2·1·c·n·j·y
C、围成图形的不都是线段,所以不是四边形;
只有B选项符合四边形的定义.
点评:理解四边形的定义,是解决本题的关键,此题属于简单题型.
3.
考点:多边形.
解析:根据多边形的定义:平面内不在一条直线上的线段首尾顺次相接组成的图形叫多边形.根据图形可知D是多边形.故选D.【来源:21·世纪·教育·网】
点评:理解多边形的概念,D中的多边形是一个凹多边形.
4.
考点:多边形.21世纪教育网
解析:根据凸多边形的定义进行判断.选项A、B、D中,画出这个多边形的任意一条边所在的直线,整个多边形都在这条直线的同一侧,所以都是凸多边形,只有C不符合凸多边形的定义,不是凸多边形.故选C.【出处:21教育名师】
点评:正确理解凸多边形的定义是解决此类问题的关键.
5.考点:等边三角形的性质.21世纪教育网
分析:由题意可知剪去的三个三角形是全等的等边三角形,可知得到剪去的小正三角的边长为5.
点评:本题主要考查等边三角形的性质,熟练掌握等边三角形的性质定理是解题的关键.
6.
考点:多边形.21世纪教育网
解答:解:如下图所示:
观察图形可知,四边形减掉一个角后,剩下的图形可能为五边形,可能为四边形,可能为三角形,
故选D.
点评:本题考查了多边形,解题的关键是能理解一个四边形减掉一个角后得到的图形的形状,通过画图的方法解决最好. 21*cnjy*com
7.考点:多边形.21世纪教育网
分析:根据凸多边形的概念,如果多边形的边都在任何一条边所在的直线的同旁,该多边形即是凸多边形.否则即是凹多边形.【来源:21cnj*y.co*m】
解答:解:选项B、C、D中,画出这个多边形的任意一条边所在的直线,整个多边形都在这条直线的同一侧,所以都是凸多边形,只有A不符合凸多边形的定义,不是凸多边形.
故选A.
点评:本题考查了多边形,正确理解凸多边形的定义是解决此类问题的关键.
8.
9.
考点:多边形.21世纪教育网
分析:根据八边形的顶点,连接点与顶点,可得答案.
解答:解:如图,故选:D.
点评:本题考查了多边形,画图是解题关键.
10.
考点:多边形.21世纪教育网
分析:根据图形的分割,可得答案.
点评:本题考查了多边形,分类讨论是解题关键.
11.
考点:多边形;多边形的对角线.21世纪教育网
分析:根据n边形的边、角、对角线,可得答案.
解答:解:是 五边形,它有五个内角,五条边,从一个顶点出发的对角线有2条,
故答案为:五,五,五,2.
点评:本题考查了多边形,n边形有n条边,n个内角,(n﹣3)条对角线.
12.
考点:多边形.21世纪教育网版权
分析:正多边形的特征是每条边都相等,每个内角都相等.
解答:解:正三角形、正方形、正六边形都属于正多边形,正多边形的特征是每条边都相等,每个内角都相等.
故答案为:(1)每条边都相等;(2)每个内角都相等.
点评:本题主要考查正多边形的性质.比较简单.
13.
考点:多边形;三角形的稳定性.21世纪教育网
点评:此题主要考查了三角形的稳定性,过n边形的一个顶点作对角线,可以做(n﹣3)条.
14.
考点:多边形;三角形的稳定性.
分析:从一个多边形的一个顶点出发,能做(n﹣3)条对角线,把三角形分成(n﹣2)个三角形.
15.
考点:多边形的对角线.21世纪教育网
分析:规律型.(1)根据图形可以得4个三角形,它与边数相等,则O是n边形内一点,连接各顶点与点O可得4个三角形;21世纪教育网版权所有
(2)根据图形可以得4个三角形,它的个数比边数小1,则点O是n边形一条边上一点,连接各顶点与点O,可以得到4个三角形;21教育网
(3)根据图形可以得到4个三角形,它的个数比边数小2,则点O与n边形的一个顶点重合时,连接各顶点与点O,可以得到4个三角形21cnjy.com
解答:解:(1)连接OA、OB、OC、OD可以得4个三角形,它与边数相等,则O是n边形内一点,连接各顶点与点O可得4个三角形;21教育名师原创作品
故答案为:4,相等,4;
(2)连接OC、OD、OE可以得4个三角形,它的个数比边数小1,则点O是n边形一条边上一点,连接各顶点与点O,可以得到4个三角形;21*cnjy*com
故答案为:4,个数比边数小1,4;
(3)过点A作六边形ABCDEF的对角线,可以得到4个三角形,它的个数比边数小2,则点O与n边形的一个顶点重合时,连接各顶点与点O,可以得到4个三角形.
故答案为:4,个数比边数小2,4.
点评:此题考查了多边形的对角线,关键是观察图形,找出三角形的个数与多边形的边数之间的关系.
16.
考点:多边形的对角线.21世纪教育网
分析:根据n边形从一个顶点出发可引出(n﹣3)条对角线,可求多边形的边数,再根据多边形的周长的定义可求这个多边形的各边长.
点评:考查了多边形的对角线,熟悉从多边形的一个顶点出发的对角线条数公式是解题关键.
17.
考点:多边形内角与外角;平行线的判定.菁优
分析:(1)首先求得∠DEA和∠EDC的度数,然后利用多边形的内角和定理可求得∠B的度数;
(2)根据∠B+∠C=180°可判定AB∥CD.
解答:证明:(1)∵∠DEF=105°,
(2)∵∠B=120°,∠C=60°,
∴∠B+∠C=180°.
∴AB∥CD.
点评:本题主要考查的是三角形的外角的性质、多边形的内角和公式、平行线的判定,求得∠DEA和∠EDC的度数是解题的关键.2-1-c-n-j-y
