5.4 不规则图形的面积 课件(共19张幻灯片)
文档属性
| 名称 | 5.4 不规则图形的面积 课件(共19张幻灯片) |
|
|
| 格式 | zip | ||
| 文件大小 | 565.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-13 00:00:00 | ||
图片预览





文档简介
课件19张PPT。第5单元 多边形面积的计算 4 不规则图形的面积学习目标1.明确不规则图形的意义。2.掌握求不规则图形面积的方法。长 方 形 的 面 积 =
正 方 形 的 面 积 =
平行四边形的面积=
三 角 形 的 面 积 =
梯 形 的 面 积 =
复习导入
你还记得哪些面积公式?长 ×宽 S=ab边长×边长 S=a×a底×高 S=ah底×高÷2 S=ah÷2(上底+下底)×高÷2
S=(a+b)h÷2情景导入1实验田大约有多大?理解题意:
因为是不规则图形,没有固定的公式来求面积。只能大致估算面积是多少。探究新知把实验田的图纸放在每个方格表示1m2的透明方格纸下。如下图:探究新知方法一:
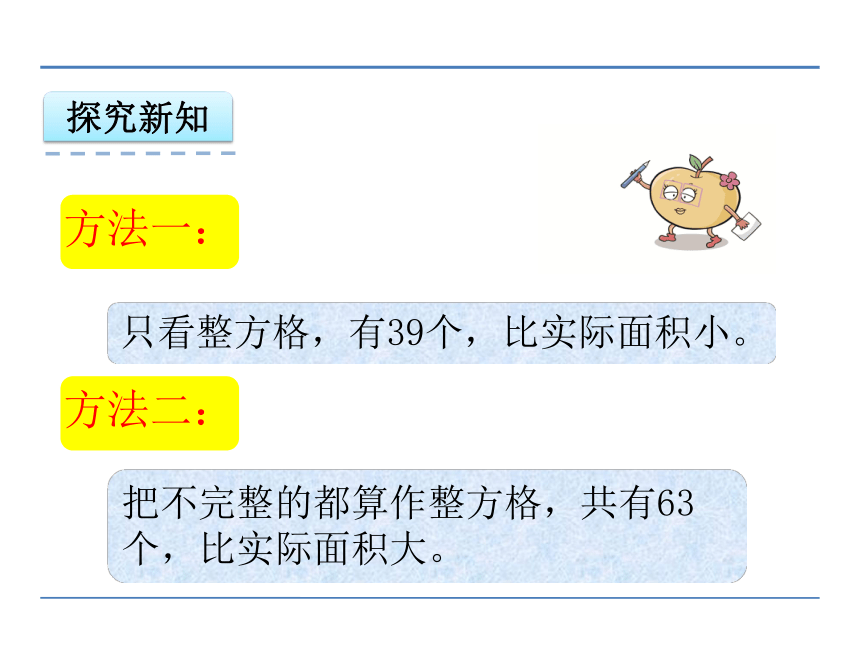
只看整方格,有39个,比实际面积小。方法二:
把不完整的都算作整方格,共有63个,比实际面积大。探究新知方法三:
先数整格,共有39个,再数不完整方格,共有24个,不完整的方格看作半格计算,24÷2=12,看做12个整方格。探究新知解决问题:
解:39+12=51(m2) 实验田大约有51m2。 答:典题精讲解题思路:1. 估算下面不规则图形的面积,每一格代表1cm2。根据不规则图形面积的估算方法。典题精讲解答: 24+8=22(cm2)解:答:该图面积大约是22平方厘米。典题精讲2.填空:下面每个小正方形格的面积是1平方厘米,求不规则图形的面积是( )平方厘米利用不规则图形面积的估算方法。解答:解答思路:19易错提醒错误原因:错在认为图形的面积一样,形状也是一样的;形状不一样的图形面积是不一样的。判断:面积相等的两个图形,形状也一定相同。 ( )
错误解答: ( √ ) ??错误解答课件PPT正确解答:( X )两个图形面积相等,形状不一定相同。易错提醒正确解答解:学以致用1.利用不规则图形面积的估算方法计算。填空:图中每个小正方形的面积表示1cm2,整格( )个,不满整格( )个,面积大约是( )cm2。24 18 3322 12 34解:学以致用2.先数满格,再数不满格。观察下图,请你填一填。满格( )个,不满格( )个,面积大约( )cm2 。(8+12÷2)×(3×3)
=14×9
=126 (m2)解:学以致用3.注意每一格边长是3厘米。计算右面土地面积。它的面积是126平方米。答:课件PPT4.假设方格纸上每方格实际面积为4平方厘米,则图中不规则图形面积大约为( )平方分米。注意单位转换。 学以致用解:0.92课件PPT根据估计不规则图形的面积方法填空。学以致用解:不完整 整 不完整 半格 除以5.填空:估计不规则图形的面积,数出( ) 方格数和( ) 方格数,把( )的方格看做( ),用半格数( )2的商加上整方格数,就是不规则图形所占的方格数。课堂小结1.a.把透明方格纸放在不规则图形的下面。b.数出不完整的方格数和整方格数,把不完整的方格看做半格,用半格数除以2的商加上整方格数,就是不规则图形所占的方格数。c.用方格数乘每个方格表示的面积,求出不规则图形的面积。2. 为提高估计的精确度,可以将图形确定为几个近似的基本图形,分别估计每部分的面积,再求它们的和。
正 方 形 的 面 积 =
平行四边形的面积=
三 角 形 的 面 积 =
梯 形 的 面 积 =
复习导入
你还记得哪些面积公式?长 ×宽 S=ab边长×边长 S=a×a底×高 S=ah底×高÷2 S=ah÷2(上底+下底)×高÷2
S=(a+b)h÷2情景导入1实验田大约有多大?理解题意:
因为是不规则图形,没有固定的公式来求面积。只能大致估算面积是多少。探究新知把实验田的图纸放在每个方格表示1m2的透明方格纸下。如下图:探究新知方法一:
只看整方格,有39个,比实际面积小。方法二:
把不完整的都算作整方格,共有63个,比实际面积大。探究新知方法三:
先数整格,共有39个,再数不完整方格,共有24个,不完整的方格看作半格计算,24÷2=12,看做12个整方格。探究新知解决问题:
解:39+12=51(m2) 实验田大约有51m2。 答:典题精讲解题思路:1. 估算下面不规则图形的面积,每一格代表1cm2。根据不规则图形面积的估算方法。典题精讲解答: 24+8=22(cm2)解:答:该图面积大约是22平方厘米。典题精讲2.填空:下面每个小正方形格的面积是1平方厘米,求不规则图形的面积是( )平方厘米利用不规则图形面积的估算方法。解答:解答思路:19易错提醒错误原因:错在认为图形的面积一样,形状也是一样的;形状不一样的图形面积是不一样的。判断:面积相等的两个图形,形状也一定相同。 ( )
错误解答: ( √ ) ??错误解答课件PPT正确解答:( X )两个图形面积相等,形状不一定相同。易错提醒正确解答解:学以致用1.利用不规则图形面积的估算方法计算。填空:图中每个小正方形的面积表示1cm2,整格( )个,不满整格( )个,面积大约是( )cm2。24 18 3322 12 34解:学以致用2.先数满格,再数不满格。观察下图,请你填一填。满格( )个,不满格( )个,面积大约( )cm2 。(8+12÷2)×(3×3)
=14×9
=126 (m2)解:学以致用3.注意每一格边长是3厘米。计算右面土地面积。它的面积是126平方米。答:课件PPT4.假设方格纸上每方格实际面积为4平方厘米,则图中不规则图形面积大约为( )平方分米。注意单位转换。 学以致用解:0.92课件PPT根据估计不规则图形的面积方法填空。学以致用解:不完整 整 不完整 半格 除以5.填空:估计不规则图形的面积,数出( ) 方格数和( ) 方格数,把( )的方格看做( ),用半格数( )2的商加上整方格数,就是不规则图形所占的方格数。课堂小结1.a.把透明方格纸放在不规则图形的下面。b.数出不完整的方格数和整方格数,把不完整的方格看做半格,用半格数除以2的商加上整方格数,就是不规则图形所占的方格数。c.用方格数乘每个方格表示的面积,求出不规则图形的面积。2. 为提高估计的精确度,可以将图形确定为几个近似的基本图形,分别估计每部分的面积,再求它们的和。
