福建省泉州市台商区惠南中学2015-2016学年高二3月月考数学(文)试题 Word版含答案
文档属性
| 名称 | 福建省泉州市台商区惠南中学2015-2016学年高二3月月考数学(文)试题 Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 133.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-13 00:00:00 | ||
图片预览



文档简介
惠南中学2016年春季高二年3月月考
数学(文科)试卷
考试时间:120分钟
满分:150分
2016.3.25
一、选择题(本题12小题,每题5
分,共60分。每小题只有一个选项符合题意,请将正确答案填入答题卷中。)
1.已知命题对任意,有,则(
)
A.存在,使
B.对任意,有
C.存在,使
D.对任意,有
2.抛物线x2=y的焦点坐标为(
)
A.(,0)
B.(0,)
C.(,0)
D.(0,)
3.设a,b∈R,“a=0”是“复数a+bi是纯虚数”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
4.已知复数z满足,则复数z等于(
)
A.1+i
B.1-i
C.2+i
D.2-i
5.在样本方差的计算公式中,数字20,40分别表示样本的( )
A.容量,方差
B.
容量,平均数
C.平均数,容量
D.标准差,平均数
6.在平面直角坐标系中,已知点,,动点满足,则点的轨迹是(
)
A.椭圆
B.双曲线
C.双曲线的左支
D.双曲线的右支
7.已知等比数列的公比为正数,且,,则( )
A.
B.
C.
D.
8.若实数满足条件,则的最小值为(
)
A.-1
B.-2
C.
D.
9.已知双曲线的离心率为,则的渐近线方程为(
)
A.
B.
C.
D.
10.已知正方形,则以为焦点,且过两点的椭圆的离心率为(
)
A.
B.
C.
D.
11.甲、乙两位同学在5次考试中的数学成绩用茎叶图表示如图,中间一列的数字表示数学成绩的十位数字,两边的数字表示数学成绩的个位数字.若甲、乙两人的平均成绩分别是、,则下列说法正确的是( )
A.
<,甲比乙成绩稳定
B.
<,乙比甲成绩稳定
C.
>,甲比乙成绩稳定
D.
>,乙比甲成绩稳定
12.若函数在(0,1)上单调递减,则实数的取值范围是(
)
A.
B.
C.
D.
二、填空题(本题6小题,每题5
分,共30分。)
13.为了调查城市PM2.
5的值,按地域把48个城市分为甲、乙、丙三组,对应的城市数分别为10,18,20.若用分层抽样的方法抽取16个城市,则乙组中应抽取的城市数为_________________.
14.双曲线的离心率为
.
15.已知为等差数列,,则
.
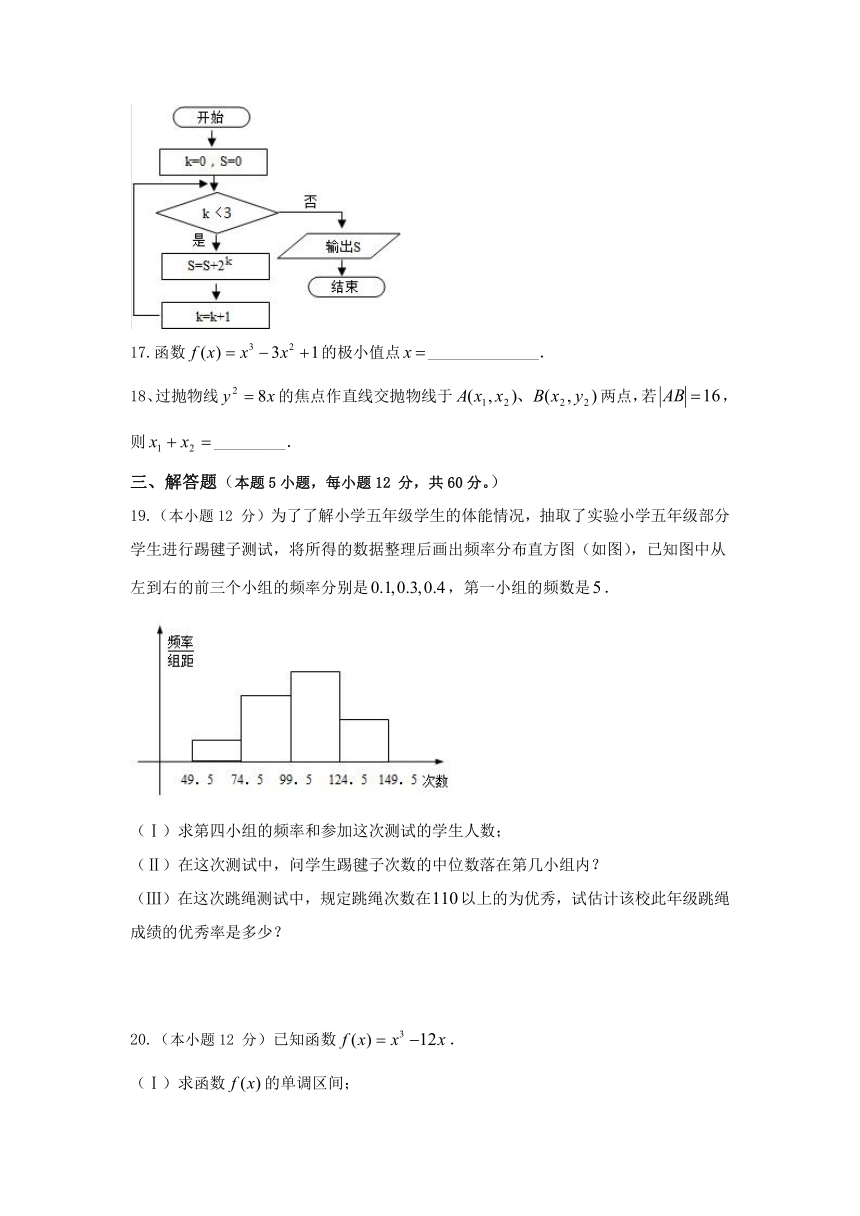
16.执行如图所示的程序框图,输出的
.
17.函数的极小值点______________.
18、过抛物线的焦点作直线交抛物线于两点,若,则_________.
三、解答题(本题5小题,每小题12
分,共60分。)
19.(本小题12
分)为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的前三个小组的频率分别是,第一小组的频数是.
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
20.(本小题12
分)已知函数.
(Ⅰ)求函数的单调区间;
(Ⅱ)当时,求的最值.
21.(本小题12
分)已知公差不为零的等差数列,若且成等比数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求数列的前n项和
22 .(本小题12
分)已知中心在坐标原点的椭圆E的长轴的一个端点是抛物线
的焦点,且椭圆E的离心率是.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点C(-1,0)的动直线与椭圆E相交于A,B两点.若线段AB的中点的横坐 标是,求直线AB的方程.
23.(本小题12
分)已知函数f(x)=,其中
(Ⅰ)若,求曲线y=f(x)在点(3,f(3))处的切线方程;
(Ⅱ)若在区间上,f(x)>0恒成立,求的取值范围.
惠南中学2016年春季高二文科数学3月月考答案
一、选择题(本题12小题,每题5
分,共60分。每小题只有一个选项符合题意,请将正确答案填入答题卷中。)
1-6 A D B B B D 7-12 C D C A B D
二、填空题(本题6小题,每题5
分,共30分。)
13. 6 14. 15. 2 16. 17. 18.
三、解答题(本题5小题,每题12
分,共60分。)
19.(Ⅰ)由题意可知第四小组的频率为
参加这次测试的学生人数为:(人) .......4分
(Ⅱ)由题意可知学生踢毽子次数的中位数落在第三小组内.......8分
(Ⅲ)因为组距为25,而110落在第三小组,所以跳绳次数在110以上的频率为
,所以估计该校此年级跳绳成绩的优秀率是43.2%. .......12分
考点:用样本的频率分布估计总体分布;频率分布直方图.
20.(1)由题意 .......2分
令得,
.......6分
(2)由下表
单调递增
单调递减
单调递增
所以极大值为,极小值为........10分
又[,所以最大值为,最小值为. .......12分
考点:1、利用导数求函数的极值及最值;2、利用导数研究函数的单调性.
21.解:(1)依题意可知,a2=1+d,a5=1+4d,
∵a1,a2,a5成等比数列,
∴(1+d)2=1+4d,即d2=2d, .......2分
解得:d=2或d=0(舍), .......4分
∴an=1+2(n﹣1)=2n﹣1; .......6分
(2)由(1)可知等差数列{an}的前n项和Pn==n2,.......8分
∵bn=2n,
∴数列{bn}的前n项和Qn==2n+1﹣2,.......10分
∴Sn=n2+2n+1﹣2. .......12分
考点:数列的求和;等差数列的通项公式.
22.(1)由题知椭圆的焦点在轴上,且又故,故椭圆的方程为. .......5分
(2)依题意,直线的斜率存在,设直线的方程为将其代入消去,整理得.......8分
设两点坐标分别为则,
故 由线段中点的横坐标是得,解得,.......10分
所以直线的方程为或.......12分
考点:1、待定系数法求椭圆方程;2、待定系数法求直线方程.
23.(Ⅰ)当a=1时,f(x)=x3-x2+1,f(3)=;
f′(x)=3x2-3x,f′(3)=18,
所以曲线y=f(x)在点(3,f(3))处的切线方程为y-=18(x-3),即.
.......5分
(Ⅱ)f′(x)=3ax2-3x=3x(ax-1),
令f′(x)=0,解得x=0或x=, .......7分
以下分两种情况讨论:
若0<a≤2,则,当x变化时,f'(x),f(x)的变化情况如下表:
当x∈时,f(x)>0等价于,即,
解不等式组得-5<a<5,因此0<a≤2; .......9分
若a>2,则,
当x变化时,f′(x),f(x)的变化情况如下表:
当x∈时,f(x)>0等价于,即,
解不等式组得或,因此2<a<5;.......11分
综合(1)和(2),可知a的取值范围为0<a<5. .......12分
考点:导函数的运用,函数的最值.
数学(文科)试卷
考试时间:120分钟
满分:150分
2016.3.25
一、选择题(本题12小题,每题5
分,共60分。每小题只有一个选项符合题意,请将正确答案填入答题卷中。)
1.已知命题对任意,有,则(
)
A.存在,使
B.对任意,有
C.存在,使
D.对任意,有
2.抛物线x2=y的焦点坐标为(
)
A.(,0)
B.(0,)
C.(,0)
D.(0,)
3.设a,b∈R,“a=0”是“复数a+bi是纯虚数”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
4.已知复数z满足,则复数z等于(
)
A.1+i
B.1-i
C.2+i
D.2-i
5.在样本方差的计算公式中,数字20,40分别表示样本的( )
A.容量,方差
B.
容量,平均数
C.平均数,容量
D.标准差,平均数
6.在平面直角坐标系中,已知点,,动点满足,则点的轨迹是(
)
A.椭圆
B.双曲线
C.双曲线的左支
D.双曲线的右支
7.已知等比数列的公比为正数,且,,则( )
A.
B.
C.
D.
8.若实数满足条件,则的最小值为(
)
A.-1
B.-2
C.
D.
9.已知双曲线的离心率为,则的渐近线方程为(
)
A.
B.
C.
D.
10.已知正方形,则以为焦点,且过两点的椭圆的离心率为(
)
A.
B.
C.
D.
11.甲、乙两位同学在5次考试中的数学成绩用茎叶图表示如图,中间一列的数字表示数学成绩的十位数字,两边的数字表示数学成绩的个位数字.若甲、乙两人的平均成绩分别是、,则下列说法正确的是( )
A.
<,甲比乙成绩稳定
B.
<,乙比甲成绩稳定
C.
>,甲比乙成绩稳定
D.
>,乙比甲成绩稳定
12.若函数在(0,1)上单调递减,则实数的取值范围是(
)
A.
B.
C.
D.
二、填空题(本题6小题,每题5
分,共30分。)
13.为了调查城市PM2.
5的值,按地域把48个城市分为甲、乙、丙三组,对应的城市数分别为10,18,20.若用分层抽样的方法抽取16个城市,则乙组中应抽取的城市数为_________________.
14.双曲线的离心率为
.
15.已知为等差数列,,则
.
16.执行如图所示的程序框图,输出的
.
17.函数的极小值点______________.
18、过抛物线的焦点作直线交抛物线于两点,若,则_________.
三、解答题(本题5小题,每小题12
分,共60分。)
19.(本小题12
分)为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的前三个小组的频率分别是,第一小组的频数是.
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在以上的为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
20.(本小题12
分)已知函数.
(Ⅰ)求函数的单调区间;
(Ⅱ)当时,求的最值.
21.(本小题12
分)已知公差不为零的等差数列,若且成等比数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求数列的前n项和
22 .(本小题12
分)已知中心在坐标原点的椭圆E的长轴的一个端点是抛物线
的焦点,且椭圆E的离心率是.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点C(-1,0)的动直线与椭圆E相交于A,B两点.若线段AB的中点的横坐 标是,求直线AB的方程.
23.(本小题12
分)已知函数f(x)=,其中
(Ⅰ)若,求曲线y=f(x)在点(3,f(3))处的切线方程;
(Ⅱ)若在区间上,f(x)>0恒成立,求的取值范围.
惠南中学2016年春季高二文科数学3月月考答案
一、选择题(本题12小题,每题5
分,共60分。每小题只有一个选项符合题意,请将正确答案填入答题卷中。)
1-6 A D B B B D 7-12 C D C A B D
二、填空题(本题6小题,每题5
分,共30分。)
13. 6 14. 15. 2 16. 17. 18.
三、解答题(本题5小题,每题12
分,共60分。)
19.(Ⅰ)由题意可知第四小组的频率为
参加这次测试的学生人数为:(人) .......4分
(Ⅱ)由题意可知学生踢毽子次数的中位数落在第三小组内.......8分
(Ⅲ)因为组距为25,而110落在第三小组,所以跳绳次数在110以上的频率为
,所以估计该校此年级跳绳成绩的优秀率是43.2%. .......12分
考点:用样本的频率分布估计总体分布;频率分布直方图.
20.(1)由题意 .......2分
令得,
.......6分
(2)由下表
单调递增
单调递减
单调递增
所以极大值为,极小值为........10分
又[,所以最大值为,最小值为. .......12分
考点:1、利用导数求函数的极值及最值;2、利用导数研究函数的单调性.
21.解:(1)依题意可知,a2=1+d,a5=1+4d,
∵a1,a2,a5成等比数列,
∴(1+d)2=1+4d,即d2=2d, .......2分
解得:d=2或d=0(舍), .......4分
∴an=1+2(n﹣1)=2n﹣1; .......6分
(2)由(1)可知等差数列{an}的前n项和Pn==n2,.......8分
∵bn=2n,
∴数列{bn}的前n项和Qn==2n+1﹣2,.......10分
∴Sn=n2+2n+1﹣2. .......12分
考点:数列的求和;等差数列的通项公式.
22.(1)由题知椭圆的焦点在轴上,且又故,故椭圆的方程为. .......5分
(2)依题意,直线的斜率存在,设直线的方程为将其代入消去,整理得.......8分
设两点坐标分别为则,
故 由线段中点的横坐标是得,解得,.......10分
所以直线的方程为或.......12分
考点:1、待定系数法求椭圆方程;2、待定系数法求直线方程.
23.(Ⅰ)当a=1时,f(x)=x3-x2+1,f(3)=;
f′(x)=3x2-3x,f′(3)=18,
所以曲线y=f(x)在点(3,f(3))处的切线方程为y-=18(x-3),即.
.......5分
(Ⅱ)f′(x)=3ax2-3x=3x(ax-1),
令f′(x)=0,解得x=0或x=, .......7分
以下分两种情况讨论:
若0<a≤2,则,当x变化时,f'(x),f(x)的变化情况如下表:
当x∈时,f(x)>0等价于,即,
解不等式组得-5<a<5,因此0<a≤2; .......9分
若a>2,则,
当x变化时,f′(x),f(x)的变化情况如下表:
当x∈时,f(x)>0等价于,即,
解不等式组得或,因此2<a<5;.......11分
综合(1)和(2),可知a的取值范围为0<a<5. .......12分
考点:导函数的运用,函数的最值.
同课章节目录
