5.2.1平行线 课件
图片预览





文档简介
(共12张PPT)
5.2.1 平行线
本课学习的内容是平行线的概念, 平行公理及其推论.这是在研究了两条直线相交的基础上进行的,是进一步研究平行关系、平行线的性质和判定, 进一步认识三角形、平行四边形、梯形等图形的特征的基础.
课件说明
学习目标:
(1)理解平行线概念, 理解平行公理,了解其推论, 会用三角尺和直尺过直线外一点画这条直线的平行线.
(2)经历动手操作、观察、归纳平行线概念及平行公理的过程,提高观察归纳、动手操作、空间想象及逻辑思维能力.
学习重点:
平行公理及其推论.
课件说明
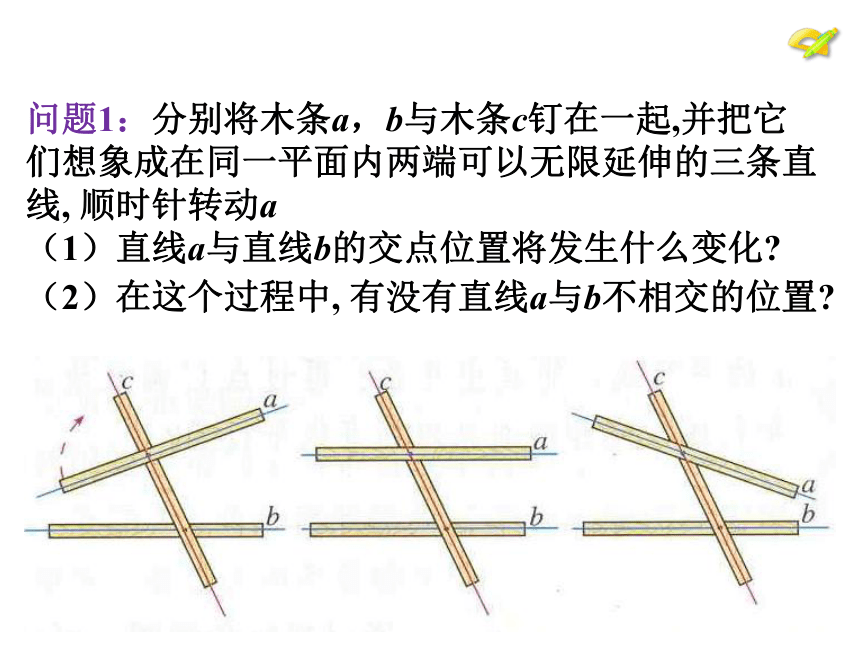
问题1:分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线, 顺时针转动a
(1)直线a与直线b的交点位置将发生什么变化
(2)在这个过程中, 有没有直线a与b不相交的位置
平行概念:同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.换言之, 同一平面内, 不相交的两条直线叫做平行线.直线a与b是平行线, 记作a∥b.
问题2:同一平面内,两条直线存在哪些位置关系
问题3:平行线在生活中很常见, 你能举出一些例子吗
相交和平行
(二)平行线画法
问题4:如何画平行线呢?给一条直线a,
你能画出直线a的平行线吗?
问题5:在转动木条a的过程中有几个位置使得直线a与b平行 过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗
(三)平行公理及其推论
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
平行公理推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.
如果b∥a,c∥a,那么b∥c.
练习:读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.
(1)
(2)
.
P
E
F
D
C
1.平面内两条直线有哪些位置关系?
2.平行公理及其推论的内容是什么?
(四)归纳小结
(五)布置作业
教科书第12页练习
5.2.1 平行线
本课学习的内容是平行线的概念, 平行公理及其推论.这是在研究了两条直线相交的基础上进行的,是进一步研究平行关系、平行线的性质和判定, 进一步认识三角形、平行四边形、梯形等图形的特征的基础.
课件说明
学习目标:
(1)理解平行线概念, 理解平行公理,了解其推论, 会用三角尺和直尺过直线外一点画这条直线的平行线.
(2)经历动手操作、观察、归纳平行线概念及平行公理的过程,提高观察归纳、动手操作、空间想象及逻辑思维能力.
学习重点:
平行公理及其推论.
课件说明
问题1:分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线, 顺时针转动a
(1)直线a与直线b的交点位置将发生什么变化
(2)在这个过程中, 有没有直线a与b不相交的位置
平行概念:同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.换言之, 同一平面内, 不相交的两条直线叫做平行线.直线a与b是平行线, 记作a∥b.
问题2:同一平面内,两条直线存在哪些位置关系
问题3:平行线在生活中很常见, 你能举出一些例子吗
相交和平行
(二)平行线画法
问题4:如何画平行线呢?给一条直线a,
你能画出直线a的平行线吗?
问题5:在转动木条a的过程中有几个位置使得直线a与b平行 过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗
(三)平行公理及其推论
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
平行公理推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.
如果b∥a,c∥a,那么b∥c.
练习:读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.
(1)
(2)
.
P
E
F
D
C
1.平面内两条直线有哪些位置关系?
2.平行公理及其推论的内容是什么?
(四)归纳小结
(五)布置作业
教科书第12页练习
