5.2.2平行线的判定(第二课时) 课件
文档属性
| 名称 | 5.2.2平行线的判定(第二课时) 课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 427.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-14 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
5.2.2 平行线的判定
(第2课时)
本课学习是在上节课的基础上通过对例题、练习的分析和讲解,进一步巩固三个判定方法,培养学生的推理能力.
课件说明
学习目标:
(1)平行线的判定方法的应用;
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力.
学习重点:
平行线判定方法的应用.
课件说明
根据定义.
根据平行公理的推论.
1.梳理旧知,归纳方法
问题1 (1)判定两条直线平行的方法有哪些?
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
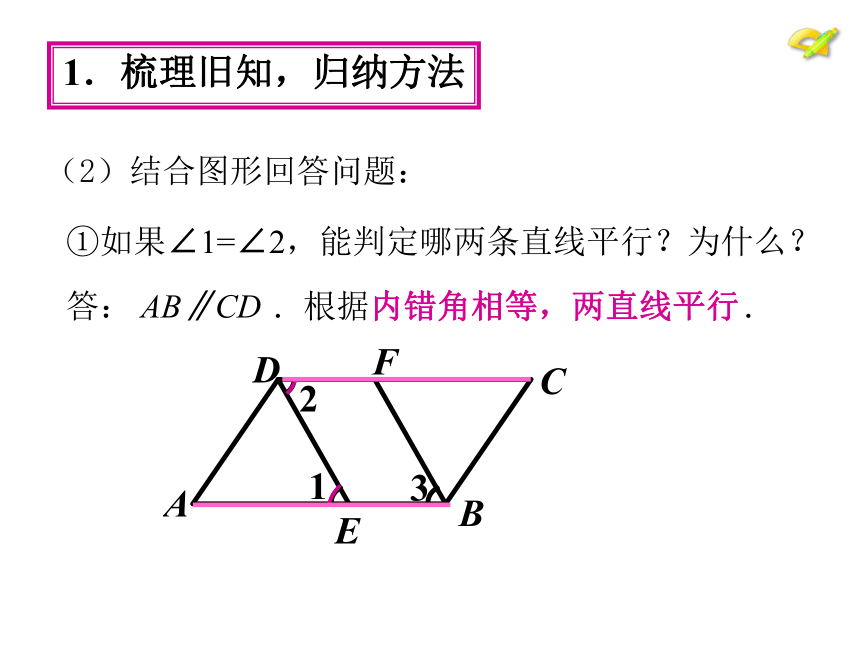
(2)结合图形回答问题:
答: AB∥CD .根据内错角相等,两直线平行.
1.梳理旧知,归纳方法
①如果∠1=∠2,能判定哪两条直线平行?为什么?
(2)结合图形回答问题:
答: DE∥FB.根据同位角相等,两直线平行.
1.梳理旧知,归纳方法
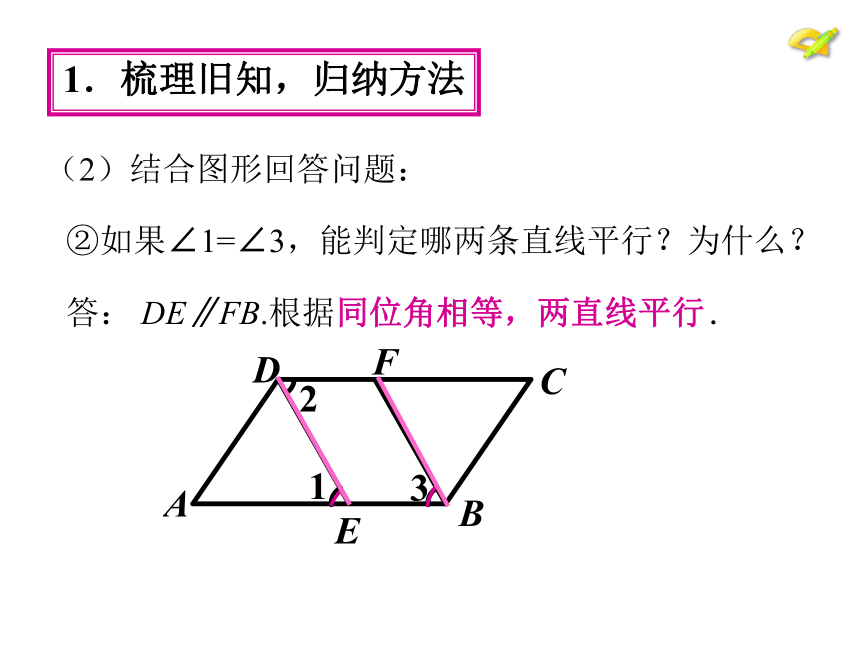
②如果∠1=∠3,能判定哪两条直线平行?为什么?
(2)结合图形回答问题:
答: AD∥CB.根据同旁内角互补,两直线平行.
1.梳理旧知,归纳方法
③如果∠A+∠ ABC=180 ,能判定哪两条直线平行?为什么?
2.学会分析,应用方法
问题2 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?
答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).
2.学会分析,应用方法
已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?
问题3 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
2.学会分析,应用方法
已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?
答:直线b与直线c平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).
1
2
你还能用其他方法说明理由吗?
3.应用迁移,深化理解
答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).
问题4 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
(1)平行线的判定方法有哪些?
4.归纳小结
(2)结合例题,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?
教科书 习题5.2 第6、10、12题
5.布置作业
5.2.2 平行线的判定
(第2课时)
本课学习是在上节课的基础上通过对例题、练习的分析和讲解,进一步巩固三个判定方法,培养学生的推理能力.
课件说明
学习目标:
(1)平行线的判定方法的应用;
(2)经历例题的分析过程,从中体会转化的思想和分析问题的方法,进一步培养推理能力.
学习重点:
平行线判定方法的应用.
课件说明
根据定义.
根据平行公理的推论.
1.梳理旧知,归纳方法
问题1 (1)判定两条直线平行的方法有哪些?
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
(2)结合图形回答问题:
答: AB∥CD .根据内错角相等,两直线平行.
1.梳理旧知,归纳方法
①如果∠1=∠2,能判定哪两条直线平行?为什么?
(2)结合图形回答问题:
答: DE∥FB.根据同位角相等,两直线平行.
1.梳理旧知,归纳方法
②如果∠1=∠3,能判定哪两条直线平行?为什么?
(2)结合图形回答问题:
答: AD∥CB.根据同旁内角互补,两直线平行.
1.梳理旧知,归纳方法
③如果∠A+∠ ABC=180 ,能判定哪两条直线平行?为什么?
2.学会分析,应用方法
问题2 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?
答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).
2.学会分析,应用方法
已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?
问题3 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
2.学会分析,应用方法
已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?
答:直线b与直线c平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).
1
2
你还能用其他方法说明理由吗?
3.应用迁移,深化理解
答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).
问题4 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
(1)平行线的判定方法有哪些?
4.归纳小结
(2)结合例题,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?
教科书 习题5.2 第6、10、12题
5.布置作业
