【苏科版】2016-2017学年上学期八年级数学第二章 轴对称图形单元检测(附答案)
文档属性
| 名称 | 【苏科版】2016-2017学年上学期八年级数学第二章 轴对称图形单元检测(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 270.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-14 11:17:59 | ||
图片预览

文档简介
第二章《轴对称图形》单元检测
(满分:100分
时间:90分钟)
一、选择题
(每题2分,共20分)
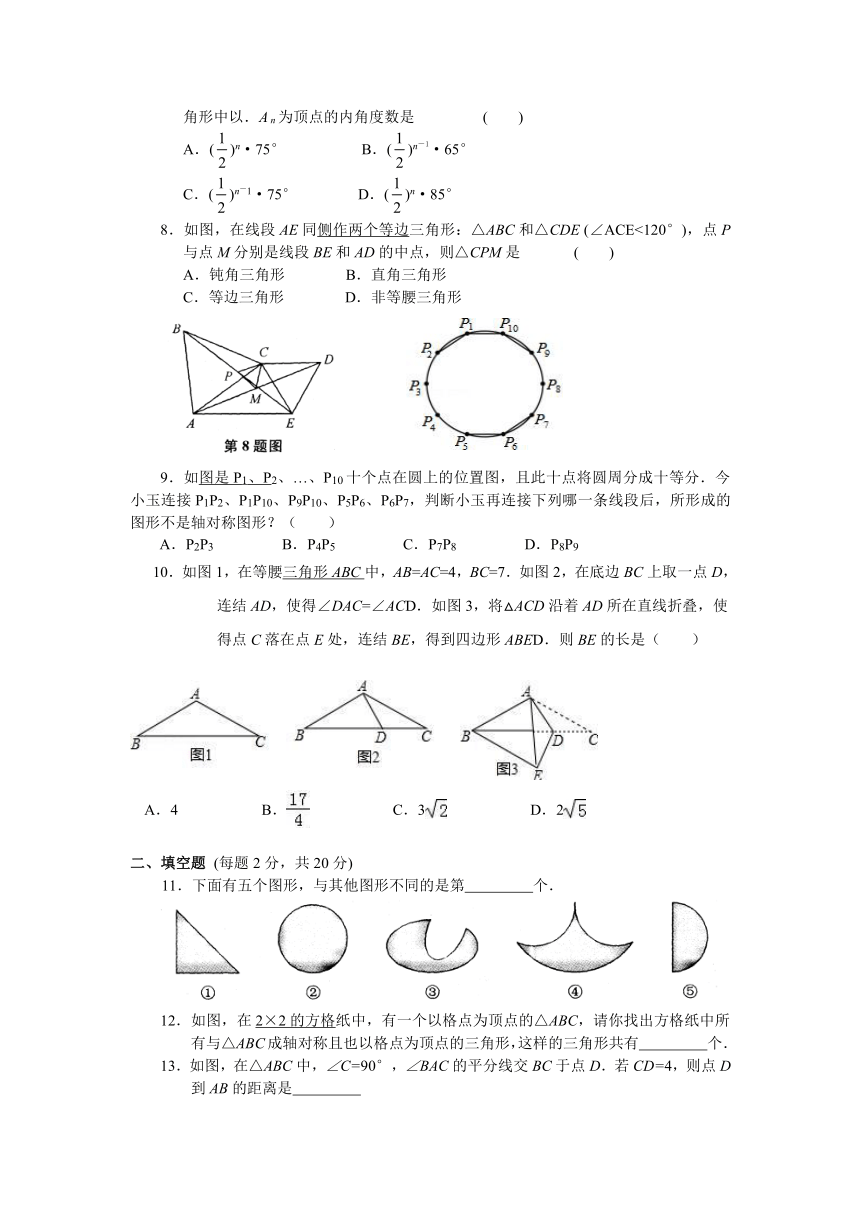
1.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是轴对称图形的是
(
)
( http: / / www.21cnjy.com )
2.一张菱形纸片按图1、图2依次对折后,再按图3打出一个圆形小孔,展开铺平后的图案是
(
)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
3.已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为
(
)
A.11
B.16
C.17
D.16或17
4.如图,在△ABC中,AB=AC,且D为边BC上一点,CD=AD,AB=BD,则∠B的度数为(
)
A.30°
B.36°
C.40°
D.45°
5.如图,已知在△ABC中,CD是AB边
( http: / / www.21cnjy.com )上的高,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于
(
)
A.10
B.7
C.5
D.4
( http: / / www.21cnjy.com )
6.如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则下列结论错误的是
(
)
A.BF=EF
B.DE=EF
C.∠EFC=45°
D.∠BEF=∠CBE
7.如图,在第1个△A1BC中,∠B=30
( http: / / www.21cnjy.com )°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2
A3=A2
E,得到第3个△A2
A3
E,…,按此做法继续下去,则第n个三角形中以.A
n为顶点的内角度数是
(
)
A.()n·75°
B.()n-1·65°
C.()n-1·75°
D.()n·85°
8.如图,在线段AE同侧作两个等边
( http: / / www.21cnjy.com )三角形:△ABC和△CDE
(∠ACE<120°),点P与点M分别是线段BE和AD的中点,则△CPM是
(
)
A.钝角三角形
B.直角三角形
C.等边三角形
D.非等腰三角形
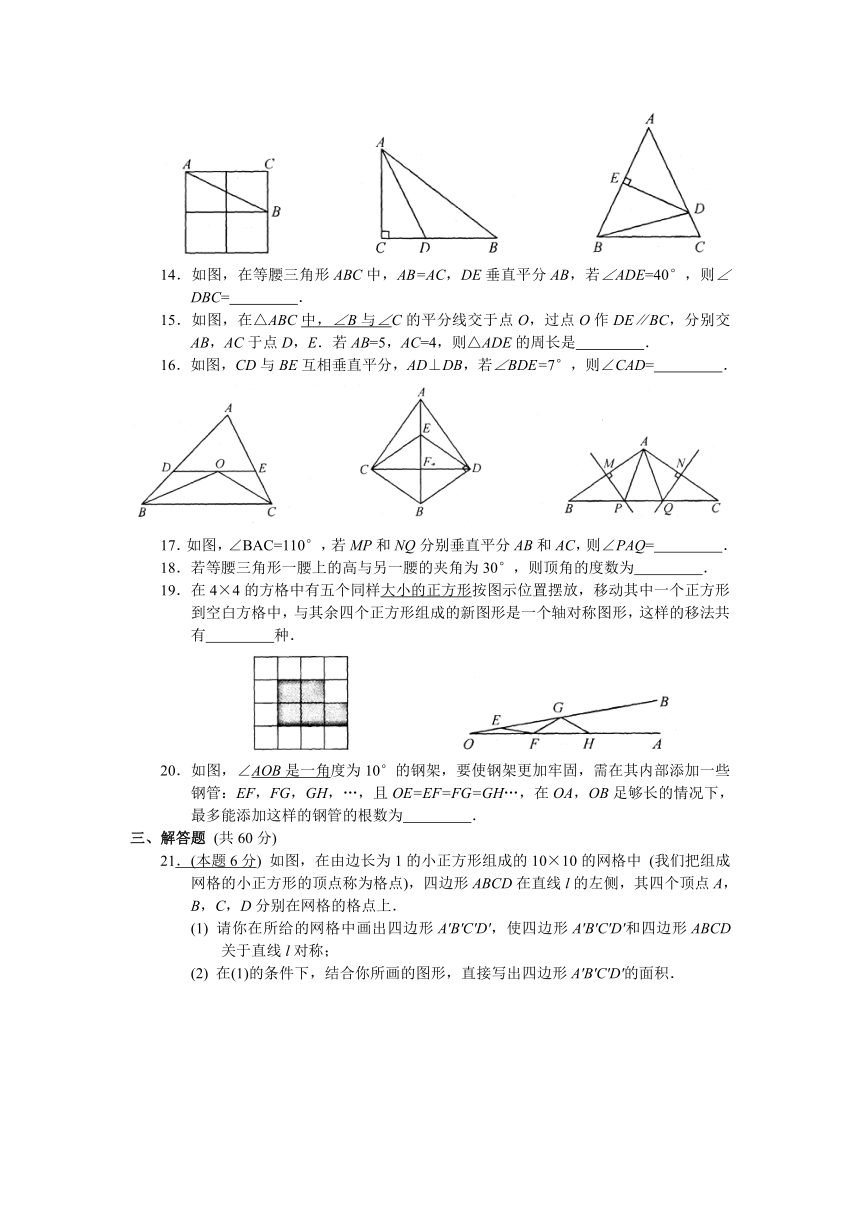
9.如图是P1、P
( http: / / www.21cnjy.com )2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
A.P2P3
B.P4P5
C.P7P8
D.P8P9
10.如图1,在等腰三角形ABC
( http: / / www.21cnjy.com )中,AB=AC=4,BC=7.如图2,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图3,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是( )
A.4
B.
C.3
D.2
二、填空题
(每题2分,共20分)
11.下面有五个图形,与其他图形不同的是第
个.
( http: / / www.21cnjy.com )
12.如图,在2×2的方格
( http: / / www.21cnjy.com )纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有
个.
13.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D.若CD=4,则点D到AB的距离是
( http: / / www.21cnjy.com )
14.如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,若∠ADE=40°,则∠DBC=
.
15.如图,在△ABC中,∠B与∠
( http: / / www.21cnjy.com )C的平分线交于点O,过点O作DE∥BC,分别交AB,AC于点D,E.若AB=5,AC=4,则△ADE的周长是
.
16.如图,CD与BE互相垂直平分,AD⊥DB,若∠BDE=7°,则∠CAD=
.
( http: / / www.21cnjy.com )
17.如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ=
.
18.若等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为
.
19.在4×4的方格中有五个同样大小的正方形
( http: / / www.21cnjy.com )按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有
种.
( http: / / www.21cnjy.com )
20.如图,∠AOB是一角
( http: / / www.21cnjy.com )度为10°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF,FG,GH,…,且OE=EF=FG=GH…,在OA,OB足够长的情况下,最多能添加这样的钢管的根数为
.
三、解答题
(共60分)
21.(本题6分
( http: / / www.21cnjy.com ))
如图,在由边长为1的小正方形组成的10×10的网格中
(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
(1)
请你在所给的网格中画出四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于直线l对称;
(2)
在(1)的条件下,结合你所画的图形,直接写出四边形A'B'C'D'的面积.
( http: / / www.21cnjy.com )
22.(本题6分)
如图,在△ABC中,∠C=90°.
(1)
用圆规和直尺在边AC上作点P,使点P到A,B的距离相等;(保留作图痕迹,不写作法和证明)
(2)
当满足(1)的点P到AB,BC的距离相等时,求∠A的度数.
( http: / / www.21cnjy.com )
23.(本题8分)
如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)
若△CMN的周长为15
cm,求AB的长;
(2)
若∠MFN=70°,求∠MCN的度数.
( http: / / www.21cnjy.com )
24.(本题8分)
如图,在△ABC中
( http: / / www.21cnjy.com ),点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)
上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形
(用序号写出所有成立的情形)
(2)
请选择(1)中的一种情形,写出证明过程.
( http: / / www.21cnjy.com )
25.(本题8分)
如图,在△ABC中
( http: / / www.21cnjy.com ),AB=AC,点D,E,F分别在边AB,BC,AC上,且BD=CE,BE=CF.如果点G为DF的中点,那么EG与DF垂直吗
请说明你的理由.
( http: / / www.21cnjy.com )
26.(本题10分)
如图,在△A
( http: / / www.21cnjy.com )BC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,连接D'C,若BD=CD'.
(1)
求证:△ABD≌△ACD';
(2)
若∠BAC=120°,求∠DAE的度数.
( http: / / www.21cnjy.com )
27.(本题12分)
如图,已知△BAD
( http: / / www.21cnjy.com )和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)
当A,B,C三点在同一直线上时
(如图1),求证:M为AN的中点.
(2)
将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时
(如图2),求证:△CAN为等腰直角三角形.
(3)
将图1中△BCE绕点B旋转到图3的位置时,(2)
中的结论是否仍然成立
若成立,试证明之;若不成立,请说明理由.
( http: / / www.21cnjy.com )
参考答案
一、选择题
1.C
2.C
3.D
( http: / / www.21cnjy.com )
4.B
5.C
6.B
7.C
8.C
(提示:△ABC和△CDE为等边三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=60°,∴∠ACE+∠ECD=∠ACE+∠ACB,即∠ACD=∠BCE,∴△ACD≌△BCE,∴AD=BE,∠CAD=∠CBE.又点P与点M分别为BE和AD的中点,∴AM=BP,∴△ACM≌△BCP,∴CM=CP,∠ACM=∠BCP,∴∠PCM=∠PCA+∠ACM=∠PCA+∠BCP=∠ACB=60°,∴△CPM是等边三角形)
9.D
10.B
二、填空题
11.③
12.5
13.4
14.15°
15.9
16.70°
17.40°
18.60°或
120°
19.13
(提示:可将图
( http: / / www.21cnjy.com )中5个阴影小正方形先编号,再依次考虑如何移动,共有13种)
20.8
(提示:当与∠AOB形成的最大三角形的外角为直角时,不能再添加钢管
三、解答题
21.(1)所作图形如下:
( http: / / www.21cnjy.com )
(2)
四边形A'B'C'D'的面积为6.5
22.(1)
(2)
连接BP.∵
点P到AB,BC的距离相等,∴
BP是
∠ABC的平分线,∴
∠ABP=∠PBC.又∵点P在线段AB的垂直平分线上,
∴
PA=PB,∴
∠A=∠ABP,∴
∠A=∠ABP=∠PBC=×90°=30°
23.(1)
∵
DM,EN分别垂直平
( http: / / www.21cnjy.com )分AC和BC,∴
AM=CM,BN=CN.∵
△CMN的周长为15cm,∴
CM+CN+MN=15
(cm),∴
AM+BN+MN=15
(cm),即AB的长为15cm
(2)
在△CMN中,∵
∠MFN=70°,∴
∠FMN+∠FNM=110°,∴
∠AMD+∠BNE=
110°.由(1)知AM=CM,BN=CN
( http: / / www.21cnjy.com ),∴
∠A
MD=∠CMD,∠BNE=∠CNE,∴
∠AMC+∠BNC=220°,∴
∠NMC+∠MNC=140°.在△CMN中,∠MCN=180°-(∠NMC+∠MNC)
=40°,即∠MCN的度数为40°
24.(1)
①②;①③
(2)
选①②
证明如下:在△BOE和△COD中,∵
∠EBO=
∠DCO,∠EOB=∠DOC
( http: / / www.21cnjy.com ),BE=CD,∴
△BOE≌△COD,∴BO=CO,∠OBC=∠OCB,∴
∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴
AB=AC,即△ABC是等腰三角形
25.EG与DF垂直.理由如下:连接D
( http: / / www.21cnjy.com )E,EF.在△ABC中,∵
AB=AC,∴
∠B=∠C.在△CEF和△BDE中,BD=CE,∠B=∠C,BE=CF,∴
△CEF≌△BDE,∴
DE=EF.又∵
点G为DF的中点,∴
EG⊥DF
26.(1)
∵
以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,∴AD=AD'.∵
在△ABD和△ACD'中,AB=AC,BD=CD',AD=AD',∴
△ABD≌△ACD'
(2)
∵
△ABD≌△ACD',∴∠BAD=∠CAD',∴
∠BAC=∠DAD'=120°.∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,∴
∠DAE=∠D'AE=∠DAD'=60°,即∠DAE=60°
27.(1)
∵
点M为DE的中点,∴
( http: / / www.21cnjy.com )
DM=ME.∵
AD∥EN,∴
∠ADM=∠NEM,又∵∠DMA=∠EMN,∴
△DMA≌△EMN,∴
AM=MN,即M为AN的中点
(2)
由(1)中△DMA≌△EMN可知DA=EN,又∵DA=AB,∴
AB=NE.∵
∠ABC=∠NEC=
135°,BC=CE,∴
△ABC≌△N
( http: / / www.21cnjy.com )EC,∴
AC=CN,∠ACB=∠NCE.∵
∠BCE=∠BCN+∠NCE=90°,∴
∠BCN+∠ACB=90°,∴
∠ACN=90°,∴
∠CAN为等腰直角三角形
(3)
由(2)可知AB=NE,BC=CE.又∵
∠ABC=360°-45°-45°-∠DBE=270°-∠DBE=270°-(180°-∠BDE-∠BED)
=90°+∠BDE+∠BED=90°+∠ADM-45°+∠BED=45°+∠MEN+∠BED=∠CEN,∴
∠ACB=∠NCE,AC=CN,∠ACN=∠ACB+∠BCN=∠BCN+∠NCE=∠BCE=90°,∴
△ABC≌△NEC,∴△CAN为等腰直角三角形,∴
(2)中的结论仍然成立
(满分:100分
时间:90分钟)
一、选择题
(每题2分,共20分)
1.下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是轴对称图形的是
(
)
( http: / / www.21cnjy.com )
2.一张菱形纸片按图1、图2依次对折后,再按图3打出一个圆形小孔,展开铺平后的图案是
(
)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
3.已知等腰三角形的两边长分别为5和6,则这个等腰三角形的周长为
(
)
A.11
B.16
C.17
D.16或17
4.如图,在△ABC中,AB=AC,且D为边BC上一点,CD=AD,AB=BD,则∠B的度数为(
)
A.30°
B.36°
C.40°
D.45°
5.如图,已知在△ABC中,CD是AB边
( http: / / www.21cnjy.com )上的高,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于
(
)
A.10
B.7
C.5
D.4
( http: / / www.21cnjy.com )
6.如图,在△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则下列结论错误的是
(
)
A.BF=EF
B.DE=EF
C.∠EFC=45°
D.∠BEF=∠CBE
7.如图,在第1个△A1BC中,∠B=30
( http: / / www.21cnjy.com )°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2
A3=A2
E,得到第3个△A2
A3
E,…,按此做法继续下去,则第n个三角形中以.A
n为顶点的内角度数是
(
)
A.()n·75°
B.()n-1·65°
C.()n-1·75°
D.()n·85°
8.如图,在线段AE同侧作两个等边
( http: / / www.21cnjy.com )三角形:△ABC和△CDE
(∠ACE<120°),点P与点M分别是线段BE和AD的中点,则△CPM是
(
)
A.钝角三角形
B.直角三角形
C.等边三角形
D.非等腰三角形
9.如图是P1、P
( http: / / www.21cnjy.com )2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
A.P2P3
B.P4P5
C.P7P8
D.P8P9
10.如图1,在等腰三角形ABC
( http: / / www.21cnjy.com )中,AB=AC=4,BC=7.如图2,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图3,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是( )
A.4
B.
C.3
D.2
二、填空题
(每题2分,共20分)
11.下面有五个图形,与其他图形不同的是第
个.
( http: / / www.21cnjy.com )
12.如图,在2×2的方格
( http: / / www.21cnjy.com )纸中,有一个以格点为顶点的△ABC,请你找出方格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有
个.
13.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D.若CD=4,则点D到AB的距离是
( http: / / www.21cnjy.com )
14.如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,若∠ADE=40°,则∠DBC=
.
15.如图,在△ABC中,∠B与∠
( http: / / www.21cnjy.com )C的平分线交于点O,过点O作DE∥BC,分别交AB,AC于点D,E.若AB=5,AC=4,则△ADE的周长是
.
16.如图,CD与BE互相垂直平分,AD⊥DB,若∠BDE=7°,则∠CAD=
.
( http: / / www.21cnjy.com )
17.如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ=
.
18.若等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为
.
19.在4×4的方格中有五个同样大小的正方形
( http: / / www.21cnjy.com )按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有
种.
( http: / / www.21cnjy.com )
20.如图,∠AOB是一角
( http: / / www.21cnjy.com )度为10°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF,FG,GH,…,且OE=EF=FG=GH…,在OA,OB足够长的情况下,最多能添加这样的钢管的根数为
.
三、解答题
(共60分)
21.(本题6分
( http: / / www.21cnjy.com ))
如图,在由边长为1的小正方形组成的10×10的网格中
(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
(1)
请你在所给的网格中画出四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于直线l对称;
(2)
在(1)的条件下,结合你所画的图形,直接写出四边形A'B'C'D'的面积.
( http: / / www.21cnjy.com )
22.(本题6分)
如图,在△ABC中,∠C=90°.
(1)
用圆规和直尺在边AC上作点P,使点P到A,B的距离相等;(保留作图痕迹,不写作法和证明)
(2)
当满足(1)的点P到AB,BC的距离相等时,求∠A的度数.
( http: / / www.21cnjy.com )
23.(本题8分)
如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)
若△CMN的周长为15
cm,求AB的长;
(2)
若∠MFN=70°,求∠MCN的度数.
( http: / / www.21cnjy.com )
24.(本题8分)
如图,在△ABC中
( http: / / www.21cnjy.com ),点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)
上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形
(用序号写出所有成立的情形)
(2)
请选择(1)中的一种情形,写出证明过程.
( http: / / www.21cnjy.com )
25.(本题8分)
如图,在△ABC中
( http: / / www.21cnjy.com ),AB=AC,点D,E,F分别在边AB,BC,AC上,且BD=CE,BE=CF.如果点G为DF的中点,那么EG与DF垂直吗
请说明你的理由.
( http: / / www.21cnjy.com )
26.(本题10分)
如图,在△A
( http: / / www.21cnjy.com )BC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,连接D'C,若BD=CD'.
(1)
求证:△ABD≌△ACD';
(2)
若∠BAC=120°,求∠DAE的度数.
( http: / / www.21cnjy.com )
27.(本题12分)
如图,已知△BAD
( http: / / www.21cnjy.com )和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)
当A,B,C三点在同一直线上时
(如图1),求证:M为AN的中点.
(2)
将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时
(如图2),求证:△CAN为等腰直角三角形.
(3)
将图1中△BCE绕点B旋转到图3的位置时,(2)
中的结论是否仍然成立
若成立,试证明之;若不成立,请说明理由.
( http: / / www.21cnjy.com )
参考答案
一、选择题
1.C
2.C
3.D
( http: / / www.21cnjy.com )
4.B
5.C
6.B
7.C
8.C
(提示:△ABC和△CDE为等边三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=60°,∴∠ACE+∠ECD=∠ACE+∠ACB,即∠ACD=∠BCE,∴△ACD≌△BCE,∴AD=BE,∠CAD=∠CBE.又点P与点M分别为BE和AD的中点,∴AM=BP,∴△ACM≌△BCP,∴CM=CP,∠ACM=∠BCP,∴∠PCM=∠PCA+∠ACM=∠PCA+∠BCP=∠ACB=60°,∴△CPM是等边三角形)
9.D
10.B
二、填空题
11.③
12.5
13.4
14.15°
15.9
16.70°
17.40°
18.60°或
120°
19.13
(提示:可将图
( http: / / www.21cnjy.com )中5个阴影小正方形先编号,再依次考虑如何移动,共有13种)
20.8
(提示:当与∠AOB形成的最大三角形的外角为直角时,不能再添加钢管
三、解答题
21.(1)所作图形如下:
( http: / / www.21cnjy.com )
(2)
四边形A'B'C'D'的面积为6.5
22.(1)
(2)
连接BP.∵
点P到AB,BC的距离相等,∴
BP是
∠ABC的平分线,∴
∠ABP=∠PBC.又∵点P在线段AB的垂直平分线上,
∴
PA=PB,∴
∠A=∠ABP,∴
∠A=∠ABP=∠PBC=×90°=30°
23.(1)
∵
DM,EN分别垂直平
( http: / / www.21cnjy.com )分AC和BC,∴
AM=CM,BN=CN.∵
△CMN的周长为15cm,∴
CM+CN+MN=15
(cm),∴
AM+BN+MN=15
(cm),即AB的长为15cm
(2)
在△CMN中,∵
∠MFN=70°,∴
∠FMN+∠FNM=110°,∴
∠AMD+∠BNE=
110°.由(1)知AM=CM,BN=CN
( http: / / www.21cnjy.com ),∴
∠A
MD=∠CMD,∠BNE=∠CNE,∴
∠AMC+∠BNC=220°,∴
∠NMC+∠MNC=140°.在△CMN中,∠MCN=180°-(∠NMC+∠MNC)
=40°,即∠MCN的度数为40°
24.(1)
①②;①③
(2)
选①②
证明如下:在△BOE和△COD中,∵
∠EBO=
∠DCO,∠EOB=∠DOC
( http: / / www.21cnjy.com ),BE=CD,∴
△BOE≌△COD,∴BO=CO,∠OBC=∠OCB,∴
∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴
AB=AC,即△ABC是等腰三角形
25.EG与DF垂直.理由如下:连接D
( http: / / www.21cnjy.com )E,EF.在△ABC中,∵
AB=AC,∴
∠B=∠C.在△CEF和△BDE中,BD=CE,∠B=∠C,BE=CF,∴
△CEF≌△BDE,∴
DE=EF.又∵
点G为DF的中点,∴
EG⊥DF
26.(1)
∵
以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,∴AD=AD'.∵
在△ABD和△ACD'中,AB=AC,BD=CD',AD=AD',∴
△ABD≌△ACD'
(2)
∵
△ABD≌△ACD',∴∠BAD=∠CAD',∴
∠BAC=∠DAD'=120°.∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,∴
∠DAE=∠D'AE=∠DAD'=60°,即∠DAE=60°
27.(1)
∵
点M为DE的中点,∴
( http: / / www.21cnjy.com )
DM=ME.∵
AD∥EN,∴
∠ADM=∠NEM,又∵∠DMA=∠EMN,∴
△DMA≌△EMN,∴
AM=MN,即M为AN的中点
(2)
由(1)中△DMA≌△EMN可知DA=EN,又∵DA=AB,∴
AB=NE.∵
∠ABC=∠NEC=
135°,BC=CE,∴
△ABC≌△N
( http: / / www.21cnjy.com )EC,∴
AC=CN,∠ACB=∠NCE.∵
∠BCE=∠BCN+∠NCE=90°,∴
∠BCN+∠ACB=90°,∴
∠ACN=90°,∴
∠CAN为等腰直角三角形
(3)
由(2)可知AB=NE,BC=CE.又∵
∠ABC=360°-45°-45°-∠DBE=270°-∠DBE=270°-(180°-∠BDE-∠BED)
=90°+∠BDE+∠BED=90°+∠ADM-45°+∠BED=45°+∠MEN+∠BED=∠CEN,∴
∠ACB=∠NCE,AC=CN,∠ACN=∠ACB+∠BCN=∠BCN+∠NCE=∠BCE=90°,∴
△ABC≌△NEC,∴△CAN为等腰直角三角形,∴
(2)中的结论仍然成立
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
