数学:3.1.3 《频率与概率》课件(新人教b版)
文档属性
| 名称 | 数学:3.1.3 《频率与概率》课件(新人教b版) |

|
|
| 格式 | rar | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-31 00:00:00 | ||
图片预览








文档简介
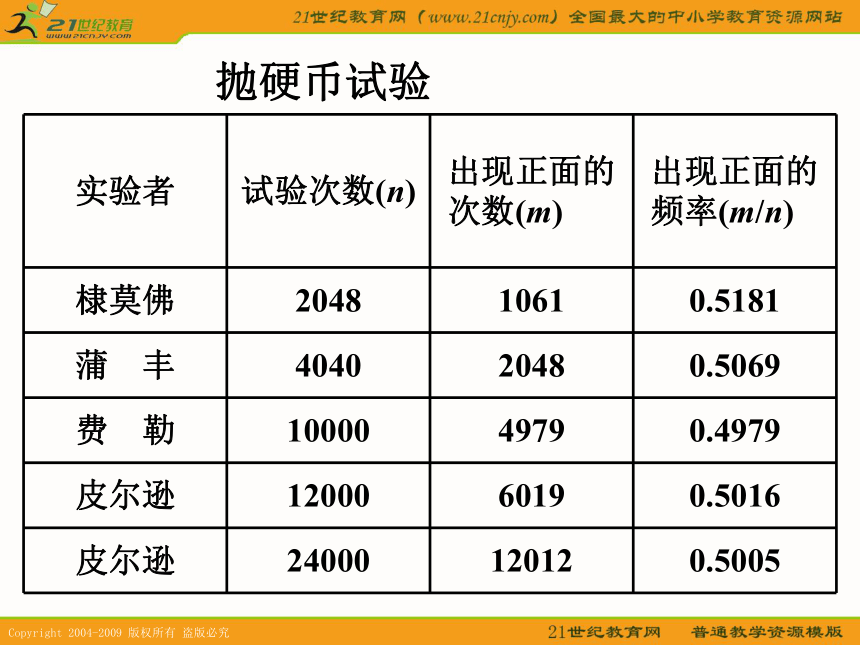
课件21张PPT。3.1.3 频率与概率 1、每人投20次,计算每个人投出正面的频率,2、每个人投50次,计算每个人投出正面的频率投掷硬币的试验:利用计算机抛硬币 历史上有些学者做过成千上万次的投掷硬币的试验。结果如下表:抛硬币试验 我们可以设想有1000人投掷硬币,如果每人投5次,计算每个人投出正面的频率,在这1000个频率中,一般说,0,0.2,0.4,0.6,0.8,1 都会有。
如果要求每个人投20次,这时频率为0,0.05,0.95,1的将会变少;多数频率在0.35~0.65之间,甚至于比较集中在0.4~0.6之间; 如果要求每人投掷1000次,这时绝大多数频率会集中在0.5附近,和0.5有较大差距的频率值也会有,但这样的频率值很少。
而且随着投掷次数的增多,频率越来越明显地集中在0.5附近。当然,即使投掷的次数再多,也不能绝对排除出现与0.5差距较大的频率值,只不过这种情形极少。 人们经过大量试验和实际经验的积累逐渐认识到:在多次重复试验中,同一事件发生的频率在某一数值附近摆动,而且随着试验次数的增加,一般摆动幅度越小,而且观察到的大偏差也越少,频率呈现一定的稳定性,频率的稳定性揭示出随机事件发生的可能性有一定的大小。事件的频率稳定在某一数值附近,我们就用这一数值表示事件发生的可能性大小。事件的概率: 一般地,在n次重复进行的试验中,事件A发生的频率 ,当n很大时,总在某个常数附近摆动,随着n的增加,摆动幅度越来越小,这时就把这个常数叫做事件A的概率,记为P(A).由定义可得概率P(A)满足:必然事件与不可能事件可看作随机事件的两种特殊情况.注意点:1.随机事件A的概率范围因此,随机事件发生的概率都满足:0≤P(A)≤12.频率与概率的关系(1)联系: 随着试验次数的增加, 频率会在概率的附近摆动,并趋于稳定.
在实际问题中,若事件的概率未知, 常用频率作为它的估计值.(2)区别: 频率本身是随机的,在试验前不能确定, 做同样次数或不同次数的重复试验得到的事件的频率都可能不同.
而概率是一个确定数,是客观存在的,与每次试验无关.例1. 为了确定某类种子的发芽率,从一大批种子中抽出若干批作发芽试验,其结果如下: 从以上的数据可以看出,这类种子的发芽率约为0.9.思考与讨论: 1、如果某种彩票的中奖概率为 ,那么买1000张这种彩票一定能中奖吗?(假设该彩票有足够多的张数。)
不一定,而有的人认为一定中奖,那么他的理由是什么呢? 这个错误产生的原因是,有人把中奖概率 理解为共有1000张彩票,其中有1张是中奖号码,然后看成不放回抽样,所以购买1000张彩票,当然一定能中奖。而实际上彩票的总张数远远大于1000。2、某地气象局预报说,明天本地降水概率为70%。你认为下面两个解释中哪一个能代表气象局的观点?
(1)明天本地有70%的区域下雨,30%的区域不下雨;
(2)明天本地下雨的机会是70%。 例如,如果天气预报说“明天降水的概率为90%”呢?降水概率的大小只能说明降水可能性的大小,概率值越大只能表示在一次试验中发生的可能性越大。在一次试验中“降水”这个事件是否发生仍然是随机的。尽管明天下雨的可能性很大,但由于“明天下雨”是随机事件,因此仍然有可能不下雨。BC3、某篮球运动员在同一条件下进行投篮练习,结果如下表:计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少?(3)这位运动员进球的概率是0.8,那么他投10次篮一定能
投中8次吗?不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的. 概率约是0.80.780.750.800.80 0.85 0.830.80做课本P97 A 1、2、31.概率是频率的稳定值,根据随机事件发生的频率只能得到概率的估计值.2.随机事件A在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率逐渐稳定在区间[0,1]内的某个常数上(即事件A的概率),这个常数越接近于1,事件A发生的概率就越大,也就是事件A发生的可能性就越大;反之,概率越接近于0,事件A发生的可能性就越小.因此,概率就是用来度量某事件发生的可能性大小的量. 课堂小结3.任何事件的概率是0~1之间的一个确定的数,
小概率(接近0)事件很少发生,大概率(接近1)事件则经常发生,知道随机事件的概率的大小有利于我们作出正确的决策. 有的同学有99%可以好好学习的概率,但却选择了1%,不思进取的概率,因为他不懂得对青春的珍惜;梦想与现实有的同学有99%对父母说句“我爱你”的概率,但却选择了1%沉默的概率。因为他还没有读懂父母对他的希冀。有的同学有99%宽宏忍让的概率,但却选择了1%翻脸的概率,因为他还不懂得宽宏的真正含义。有的同学有99%帮助别人的概率,但却选择了1%麻木不仁的概率,因为他还没有领会生命的真谛。
如果要求每个人投20次,这时频率为0,0.05,0.95,1的将会变少;多数频率在0.35~0.65之间,甚至于比较集中在0.4~0.6之间; 如果要求每人投掷1000次,这时绝大多数频率会集中在0.5附近,和0.5有较大差距的频率值也会有,但这样的频率值很少。
而且随着投掷次数的增多,频率越来越明显地集中在0.5附近。当然,即使投掷的次数再多,也不能绝对排除出现与0.5差距较大的频率值,只不过这种情形极少。 人们经过大量试验和实际经验的积累逐渐认识到:在多次重复试验中,同一事件发生的频率在某一数值附近摆动,而且随着试验次数的增加,一般摆动幅度越小,而且观察到的大偏差也越少,频率呈现一定的稳定性,频率的稳定性揭示出随机事件发生的可能性有一定的大小。事件的频率稳定在某一数值附近,我们就用这一数值表示事件发生的可能性大小。事件的概率: 一般地,在n次重复进行的试验中,事件A发生的频率 ,当n很大时,总在某个常数附近摆动,随着n的增加,摆动幅度越来越小,这时就把这个常数叫做事件A的概率,记为P(A).由定义可得概率P(A)满足:必然事件与不可能事件可看作随机事件的两种特殊情况.注意点:1.随机事件A的概率范围因此,随机事件发生的概率都满足:0≤P(A)≤12.频率与概率的关系(1)联系: 随着试验次数的增加, 频率会在概率的附近摆动,并趋于稳定.
在实际问题中,若事件的概率未知, 常用频率作为它的估计值.(2)区别: 频率本身是随机的,在试验前不能确定, 做同样次数或不同次数的重复试验得到的事件的频率都可能不同.
而概率是一个确定数,是客观存在的,与每次试验无关.例1. 为了确定某类种子的发芽率,从一大批种子中抽出若干批作发芽试验,其结果如下: 从以上的数据可以看出,这类种子的发芽率约为0.9.思考与讨论: 1、如果某种彩票的中奖概率为 ,那么买1000张这种彩票一定能中奖吗?(假设该彩票有足够多的张数。)
不一定,而有的人认为一定中奖,那么他的理由是什么呢? 这个错误产生的原因是,有人把中奖概率 理解为共有1000张彩票,其中有1张是中奖号码,然后看成不放回抽样,所以购买1000张彩票,当然一定能中奖。而实际上彩票的总张数远远大于1000。2、某地气象局预报说,明天本地降水概率为70%。你认为下面两个解释中哪一个能代表气象局的观点?
(1)明天本地有70%的区域下雨,30%的区域不下雨;
(2)明天本地下雨的机会是70%。 例如,如果天气预报说“明天降水的概率为90%”呢?降水概率的大小只能说明降水可能性的大小,概率值越大只能表示在一次试验中发生的可能性越大。在一次试验中“降水”这个事件是否发生仍然是随机的。尽管明天下雨的可能性很大,但由于“明天下雨”是随机事件,因此仍然有可能不下雨。BC3、某篮球运动员在同一条件下进行投篮练习,结果如下表:计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少?(3)这位运动员进球的概率是0.8,那么他投10次篮一定能
投中8次吗?不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的. 概率约是0.80.780.750.800.80 0.85 0.830.80做课本P97 A 1、2、31.概率是频率的稳定值,根据随机事件发生的频率只能得到概率的估计值.2.随机事件A在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率逐渐稳定在区间[0,1]内的某个常数上(即事件A的概率),这个常数越接近于1,事件A发生的概率就越大,也就是事件A发生的可能性就越大;反之,概率越接近于0,事件A发生的可能性就越小.因此,概率就是用来度量某事件发生的可能性大小的量. 课堂小结3.任何事件的概率是0~1之间的一个确定的数,
小概率(接近0)事件很少发生,大概率(接近1)事件则经常发生,知道随机事件的概率的大小有利于我们作出正确的决策. 有的同学有99%可以好好学习的概率,但却选择了1%,不思进取的概率,因为他不懂得对青春的珍惜;梦想与现实有的同学有99%对父母说句“我爱你”的概率,但却选择了1%沉默的概率。因为他还没有读懂父母对他的希冀。有的同学有99%宽宏忍让的概率,但却选择了1%翻脸的概率,因为他还不懂得宽宏的真正含义。有的同学有99%帮助别人的概率,但却选择了1%麻木不仁的概率,因为他还没有领会生命的真谛。
