第三章《位置与坐标》单元检测卷

【新北师大版八年级上数学】
第三章《位置与坐标》单元检测卷
（全卷满分100分 限时90分钟）
一.选择题（每小题3分36分）
1．如果座位表上“5列2行”记作（5，2），那么（4，3）表示（ ）
A．3列5行 B．5列3行 C．4列3行 D．3列4行
2．气象台为预测台风，首先要确定台风中心的位置，下列说法能确定台风中心位置的是（）
A.距台湾200海里 B.位于台湾与海口之间 C.位于东经120.8度，北纬32.8度
D.位于西太平洋
3．如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是（ ）

A．西偏北30° B．北偏西60° C．北偏东30° D．东偏北60°
4．已知：岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，符合条件的示意图是（ ）21·世纪*教育网
A．B．C．D．
5．如图1是一局围棋比赛的几手棋.为记录棋谱方便，横线用数字表示，纵线用字母表示，这样，黑棋的位置可记为（B,2），白棋②的位置可记为(D,1)，则白棋⑨的位置应记为（ ）
A．（C，5） B．(C，4) C．(4，C) D．(5，C)
6．如图，小手盖住的点的坐标可能为（ ）
A．（4，3） B．（﹣4，3） C．（﹣4，﹣3） D．（4，﹣3）
7．平面直角坐标系中，在第四象限的点是（ ）
A．（1，2） B．（1，－2） C．（－1，2） D．（－1，－2）
8．已知点P（2﹣4m，m﹣4）在第三象限，且满足横、纵坐标均为整数的点P有（ ）
A．1个 B．2个 C．3个 D．4个
9．将平面直角坐标系内某图形上各个点的纵坐标都乘以﹣1，横坐标不变，所得图形与原图形的关系是（ ）
A．关于y轴对称
B．关于x轴对称
C．沿x轴向左平移1个单位长度
D．沿y轴向下平移1个单位长度
10．如图，∠ACB＝90o，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为 （ ）
A． B． C． D．
11．如图：△ABC的周长为30cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边与点E，连接AD，若AE=4cm，则△ABD的周长是（ ）
A．22cm B．20cm C．18cm D．15cm
12．如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA1A2B1，…，依此规律，则点A8的坐标是（ ）
A.（﹣8，0） B.（0，8） C.（0，8） D.（0，16）
二.填空题：（每小题3分共12分）
13．若a＞0，b＜﹣2，则点（a，b+2）应在第 象限．
14．如图所示的象棋盘上，若“士”的坐标是（﹣2，﹣2），“相”的坐标是（3，2），则“炮”的坐标是 ．【来源：21·世纪·教育·网】
15．已知P1（a，-1）和P2（2，b）关于原点对称，则（a+b）2016= ．
16． 如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上．顶点B的坐标为（3，），点C的坐标为（1，0），且∠AOB=30°点P为斜边OB上的一个动点，则PA+PC的最小值为____ _____．21教育名师原创作品
三.解答题：(共52分)
17．（6分）已知点A（2a＋1，a＋7）到x轴、y轴的距离相等，求a的值．
18．（6分）△ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．
（1）作出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；
（2）作出△ABC关于y对称的△A2B2C2，并写出点C2的坐标．
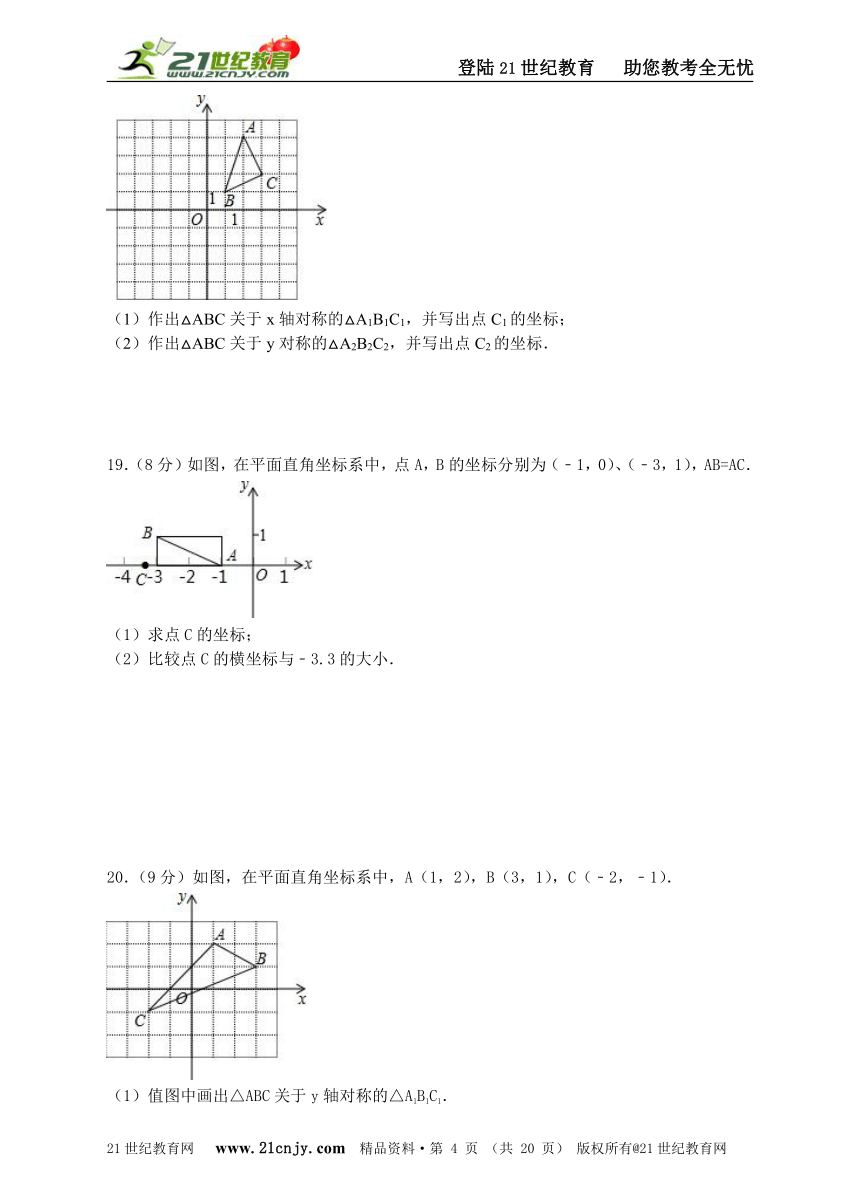
19．（8分）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0）、（﹣3，1），AB=AC．
（1）求点C的坐标；
（2）比较点C的横坐标与﹣3.3的大小．
20．（9分）如图，在平面直角坐标系中，A（1，2），B（3，1），C（﹣2，﹣1）．
（1）值图中画出△ABC关于y轴对称的△A1B1C1．
（2）分别写出A1、B1、C1三点的坐标．
（3）求S△ABC．
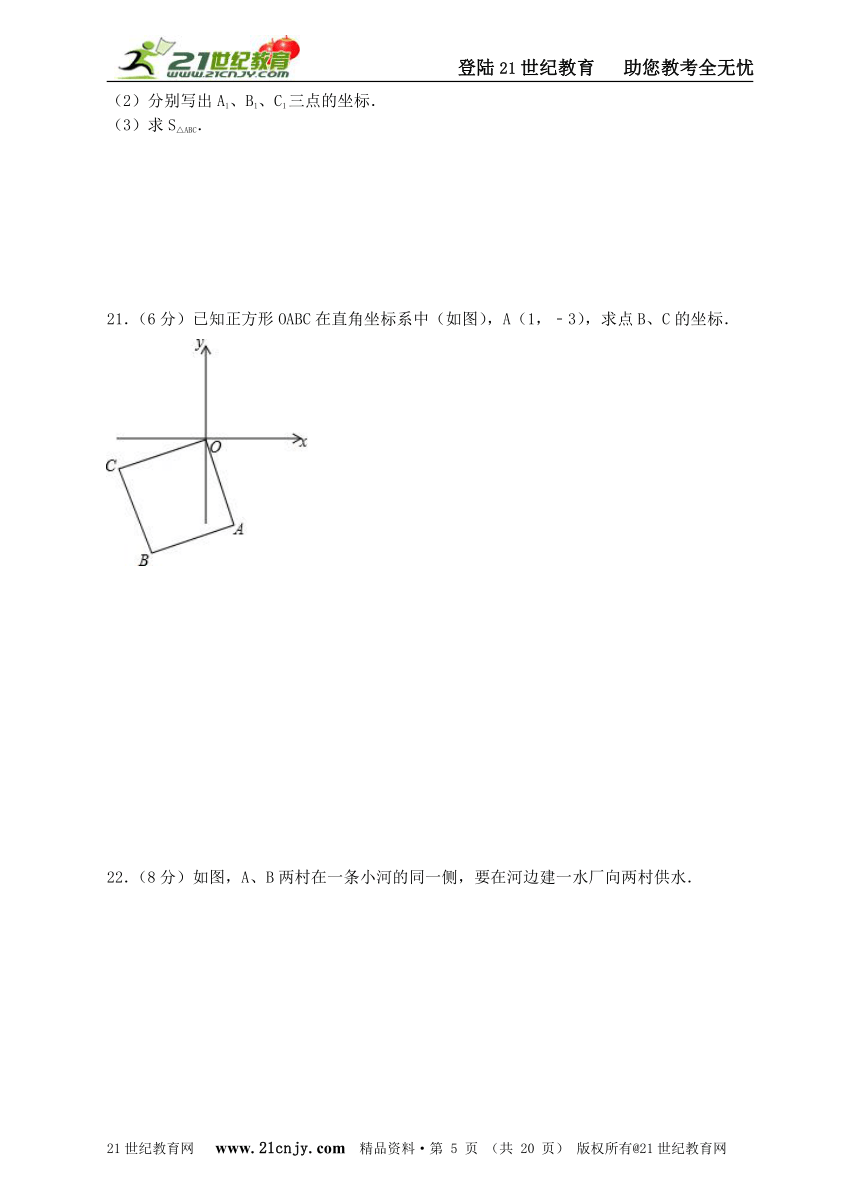
21．（6分）已知正方形OABC在直角坐标系中（如图），A（1，﹣3），求点B、C的坐标．
22．（8分）如图，A、B两村在一条小河的同一侧，要在河边建一水厂向两村供水．
（1）若要使自来水厂到两村的距离相等，厂址应选在哪个位置？
（2）若要使自来水厂到两村的输水管用料最省，厂址应选在哪个位置？请将上述两种情况下的自来水厂厂址标出，并保留作图痕迹．21cnjy.com
23．（9分）如图①，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）2+=0，过C作CB⊥x轴于B．www.21-cn-jy.com
（1）求三角形ABC的面积．
（2）在y轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．www-2-1-cnjy-com
（3）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图②，求∠AED的度数．　　21*cnjy*com
答案与解析
一.选择题（每小题3分36分）
1．如果座位表上“5列2行”记作（5，2），那么（4，3）表示（ ）
A．3列5行 B．5列3行 C．4列3行 D．3列4行
【答案】C
【解析】
试题分析：直角坐标系中，坐标平面内的点与有序实数对一一对应；记住各象限内点的坐标特征和坐标轴上点的坐标特征．若座位表上“5列2行”记作（5，2），那么（4，3）表示4列3行．【出处：21教育名师】
2．气象台为预测台风，首先要确定台风中心的位置，下列说法能确定台风中心位置的是（）
A.距台湾200海里 B.位于台湾与海口之间 C.位于东经120.8度，北纬32.8度
D.位于西太平洋
【答案】C．
【解析】
试题分析：根据坐标确定位置，需要横向与纵向的两个数据解答．
A、距台湾200海里，位置不确定，故本选项错误；
B、位于台湾与海口之间，位置不确定，故本选项错误；
C、位于东经120.8度，北纬32.8度，位置非常明确，故本选项正确；
D、位于西太平洋，位置不确定，故本选项错误．
故选C．
3．如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是（ ）

A．西偏北30° B．北偏西60° C．北偏东30° D．东偏北60°
【答案】B
【解析】
试题分析：如图，由题意可得∠AOB=90°，所以∠1=90°-30°=60°，所以OB为北偏西60°，故选：B．
4．已知：岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，符合条件的示意图是（ ）
A．B．C．D．
【答案】D
【解析】
试题分析：根据文字语言，画出示意图，如下：
故选：D
5．如图1是一局围棋比赛的几手棋.为记录棋谱方便，横线用数字表示，纵线用字母表示，这样，黑棋的位置可记为（B,2），白棋②的位置可记为(D,1)，则白棋⑨的位置应记为（ ）
A．（C，5） B．(C，4) C．(4，C) D．(5，C)
【答案】B．
【解析】
试题分析：∵黑棋的位置可记为（B，2），
∴白棋⑨的位置应记为（C，4）．
故选B．
6．如图，小手盖住的点的坐标可能为（ ）
A．（4，3） B．（﹣4，3） C．（﹣4，﹣3） D．（4，﹣3）
【答案】C
【解析】
试题分析：根据第三象限内点的横坐标小于零，纵坐标小于零，可得答案．
解：A、（4，3）在第一象限，故A错误；
B、（﹣4，3）在第二象限，故B错误；
C、（﹣4，﹣3）在第三象限，故C正确；
D、（4，﹣3）在第四象限，故D错误；
故选：C．
7．平面直角坐标系中，在第四象限的点是（ ）
A．（1，2） B．（1，－2） C．（－1，2） D．（－1，－2）
【答案】B
【解析】
试题分析：根据坐标点的象限特点：第一象限（+，+），第二象限（-，+），第三象限（-，-），第四象限（+，-），故可知（-1，-2）在第四象限．2-1-c-n-j-y
故选D
8．已知点P（2﹣4m，m﹣4）在第三象限，且满足横、纵坐标均为整数的点P有（ ）
A．1个 B．2个 C．3个 D．4个
【答案】C．
【解析】
试题分析：已知点P（2﹣4m，m﹣4）在第三象限，即可得2-4m＜0，m-4＜0，解得＜m＜4，因为点P为整数，所以满足横、纵坐标均为整数的点P有3个，分别为1、2、3，故答案选C．21*cnjy*com
9．将平面直角坐标系内某图形上各个点的纵坐标都乘以﹣1，横坐标不变，所得图形与原图形的关系是（ ）
A．关于y轴对称
B．关于x轴对称
C．沿x轴向左平移1个单位长度
D．沿y轴向下平移1个单位长度
【答案】B
【解析】
试题分析：根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得答案．
解：将平面直角坐标系内某图形上各个点的纵坐标都乘以﹣1，横坐标不变，所得图形与原图形的关系是关于x轴对称，
故选：B．
10．如图，∠ACB＝90o，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为 （ ）
A． B． C． D．
【答案】B.
【解析】
试题分析：Rt△ABC中，由勾股定理可得AB=5.根据折叠的性质可得AE=ED，AC=CD，CE⊥AD，∠ACE＝∠CED，∠BCF＝∠B′CF，BF=B′F；根据S△ABC=AC×BC=AB×CE可求得CE=.在Rt△ACE中，再根据勾股定理可求得AE=，又因∠ACE+∠CED+∠BCF+∠B′CF=∠ACB＝90o，所以∠ECF=∠ACB＝45o，即△ECF为等腰直角三角形，所以CE=EF=，因此BF=AB-AE-EF=5--=，所以B′F=BF=，故答案选B.
11．如图：△ABC的周长为30cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边与点E，连接AD，若AE=4cm，则△ABD的周长是（ ）
A．22cm B．20cm C．18cm D．15cm
【答案】A
【解析】
试题分析：由图形和题意可知AD=DC，AE=CE=4，AB+BC=22，△ABD的周长=AB+AD+BD=AB+CD+BC﹣CD=AB+BC，即可求出周长为22．
解：∵AE=4cm，
∴AC=8，
∵△ABC的周长为30cm，
∴AB+BC=22，
∵△ABD的周长=AB+AD+BD，AD=DC，
∴△ABD的周长=AB+AD+BD=AB+CD+BC﹣CD=AB+BC=22
故选择A．
12．如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA1A2B1，…，依此规律，则点A8的坐标是（ ）
A.（﹣8，0） B.（0，8） C.（0，8） D.（0，16）
【答案】D．
【解析】
试题分析：根据题意和图形可看出每经过一次变化，都顺时针旋转45°，边长都乘以，
∵从A到A3经过了3次变化，∵45°×3=135°，1×（）3=2．
∴点A3所在的正方形的边长为2，点A3位置在第四象限．
∴点A3的坐标是（2，﹣2）；
可得出：A1点坐标为（1，1），
A2点坐标为（0，2），
A3点坐标为（2，﹣2），
A4点坐标为（0，﹣4），A5点坐标为（﹣4，﹣4），
A6（﹣8，0），A7（﹣8，8），A8（0，16），
故选：D．
二.填空题：（每小题3分共12分）
13．若a＞0，b＜﹣2，则点（a，b+2）应在第 象限．
【答案】四．
【解析】
试题分析：根据b＜﹣2确定出b+2＜0，然后根据各象限内点的坐标特征解答．
解：∵b＜﹣2，
∴b+2＜0，
又∵a＞0，
∴点（a，b+2）应在第四象限．
故答案为：四．
14．如图所示的象棋盘上，若“士”的坐标是（﹣2，﹣2），“相”的坐标是（3，2），则“炮”的坐标是 ．21·cn·jy·com
【答案】（﹣3，0）．
【解析】
试题分析：根据“士”的坐标向右移动两个单位，再向上移动两个单位，可得原点，根据“炮”的位置，可得答案．【版权所有：21教育】
解：如图：
，
“炮”的坐标是 （﹣3，0），
故答案为：（﹣3，0）．
15．已知P1（a，-1）和P2（2，b）关于原点对称，则（a+b）2016= ．
【答案】1．
【解析】
试题解析：由P1（a，-1）和P2（2，b）关于原点对称，得
a=-2，b=-（-1）=1．
（a+b）2016=（-1）2016=1．
16． 如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上．顶点B的坐标为（3，），点C的坐标为（1，0），且∠AOB=30°点P为斜边OB上的一个动点，则PA+PC的最小值为____ _____．
【答案】
【解析】
试题分析：作A关于OB的对称点D，连接CD交OB于P，连接AP，过D作DN⊥OA于N，则此时PA+PC的值最小．
∵DP=PA，∴PA+PC=PD+PC=CD．
∵B（3，），∴AB=，OA=3，∠B=60°．
由勾股定理得：OB=2．
由三角形面积公式得：×OA×AB=×OB×AM，∴AM=．∴AD=2×=3．
∵∠AMB=90°，∠B=60°，∴∠BAM=30°．
∵∠BAO=90°，∴∠OAM=60°．
∵DN⊥OA，∴∠NDA=30°．∴AN=AD=．
由勾股定理得：DN=．
∵C（1，0），∴CN=3-1-=．
在Rt△DNC中，由勾股定理得：DC=．
∴PA+PC的最小值是．
三.解答题：(共52分)
17．（6分）已知点A（2a＋1，a＋7）到x轴、y轴的距离相等，求a的值．
【答案】6或
【解析】因为点A（2a＋1，a＋7）到x轴、y轴的距离相等，所以|2a＋1|＝|a＋7|，所以2a＋1＝a＋7或2a＋1＋a＋7＝0，解得a＝6或．
18．（6分）△ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．
（1）作出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；
（2）作出△ABC关于y对称的△A2B2C2，并写出点C2的坐标．
【答案】（1）作图见解析，点C1的坐标（3，﹣2）；
（2）作图见解析，点C2的坐标 （﹣3，2）．
【解析】
试题分析：（1）根据关于x轴对称的点的坐标特点画出△A1B1C1，并写出点C1的坐标即可；
（2）根据关于y轴对称的点的坐标特点画出△A2B2C2，并写出点C2的坐标即可．
解：（1）如图所示，点C1的坐标（3，﹣2）；
（2）如图2所示，点C2的坐标 （﹣3，2）．
19．（8分）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0）、（﹣3，1），AB=AC．
（1）求点C的坐标；
（2）比较点C的横坐标与﹣3.3的大小．
【答案】（1）点C的坐标为（﹣1﹣，0）；（2）C的横坐标＞﹣3.3．
【解析】
试题分析：（1）由勾股定理得出AB=AC==，求出OC=1+，即可得出点C的坐标；
（2）由≈2.236，得出|1+|＜3.3，即可得出结果．
解：（1）由勾股定理得：AB=AC==，
∴OC=1+，
∴点C的坐标为（﹣1﹣，0）；
（2）∵≈2.236，
∴|1+|＜3.3，
∴﹣1﹣＞﹣3.3，
即C的横坐标＞﹣3.3．
20．（9分）如图，在平面直角坐标系中，A（1，2），B（3，1），C（﹣2，﹣1）．
（1）值图中画出△ABC关于y轴对称的△A1B1C1．
（2）分别写出A1、B1、C1三点的坐标．
（3）求S△ABC．
【答案】（1）见解析；（2）A1（﹣1，2），B1（﹣3，1），C1（2，﹣1）；（3）．
【解析】
试题分析：（1）分别作出各点关于y轴的对称点，再顺次连接即可；
（2）根据各点在坐标系中的位置写出各点坐标即可；
（3）利用矩形的面积减去三个顶点上三角形的面积即可．
解：（1）如图所示；
（2）由图可知，A1（﹣1，2），B1（﹣3，1），C1（2，﹣1）；
（3）S△ABC=3×5﹣×2×1﹣×3×3﹣×2×5=．
21．（6分）已知正方形OABC在直角坐标系中（如图），A（1，﹣3），求点B、C的坐标．
【答案】B（﹣2，﹣4），C（﹣3，﹣1）
【解析】
试题分析：作AD⊥x轴于D，CE⊥x轴于E，BF⊥CE于F，如图，根据正方形的性质得OC=OA，∠AOC=90°，则利用同角的余角相等得∠OAD=∠EOC，则可根据“AAS”判断△COE≌△OAD，所以OE=AD=3，CE=OD=1，同样方法可证得△BFC≌△CEO，则BF=CE=1，CF=OE=3，然后利用第三象限点的坐标特征写出B、C点坐标．21世纪教育网版权所有
解：作AD⊥x轴于D，CE⊥x轴于E，BF⊥CE于F，如图，
∵A点坐标为（1，﹣3），
∴OD=1，AD=3，
∵四边形ABCD为正方形，
∴OC=OA，∠AOC=90°，
∵∠EOC+∠AOD=90°，∠AOD+∠OAD=90°，
∴∠OAD=∠EOC，
在△COE和△OAD中
，
∴△COE≌△OAD，
∴OE=AD=3，CE=OD=1，
∴C（﹣3，﹣1），
同样方法可证得△BFC≌△CEO，
∴BF=CE=1，CF=OE=3，
∴B（﹣2，﹣4）．
22．（8分）如图，A、B两村在一条小河的同一侧，要在河边建一水厂向两村供水．
（1）若要使自来水厂到两村的距离相等，厂址应选在哪个位置？
（2）若要使自来水厂到两村的输水管用料最省，厂址应选在哪个位置？请将上述两种情况下的自来水厂厂址标出，并保留作图痕迹．21教育网
【答案】
【解析】
试题分析：根据中垂线和轴对称及三角形的三边关系求解．
试题解析：解：（1）根据中垂线的性质：中垂线上的点到线段两个端点的距离相等知，
作出AB的中垂线与河岸交于点P，则点P满足到AB的距离相等．
（2）作出点A关于河岸的对称点C，连接CB，交于河岸于点P，则点P能满足AP+PB最小，
理由：连接AP，AP=PC，三角形的任意两边之和大于第三边，当点P在CB的连线上时，CP+BP是最小的．2·1·c·n·j·y
23．（9分）如图①，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）2+=0，过C作CB⊥x轴于B．【来源：21cnj*y.co*m】
（1）求三角形ABC的面积．
（2）在y轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．
（3）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图②，求∠AED的度数．
【答案】（1）4；（2）存在．（0，3），（0，﹣1）；（3）45°
【解析】
试题分析：（1）根据非负数的性质求出a，b的值，进而得出A（﹣2，0），C（2，2），B（2，0），然后根据三角形面积公式计算S△ABC；
（2）如图③，AC交y轴于Q，先确定Q（0，1），设P（0，t），利用S△PAC=S△APQ+S△CPQ=S△ABC得出关于t的方程，然后解方程求出t即可得到P点坐标；
（3）如图②，作EM∥AC，然后根据平行线的性质和角的平分线，得出∠AED=（∠CAB+∠ODB），而由AC∥BD得到∠CAB=∠OBD，于是∠CAB+∠ODB=∠OBD+∠ODB=90°，则∠AED=45°．
试题解析：（1）∵（a+2）2+=0，
∴a+2=0，b﹣2=0，解得a=﹣2，b=2，
∴A（﹣2，0），C（2，2），
∵CB⊥x轴，
∴B（2，0），
∴S△ABC=×（2+2）×2=4；
（2）存在．
如图③，AC交y轴于Q，则Q（0，1），
设P（0，t），
∵S△PAC=S△APQ+S△CPQ=S△ABC，
∴?|t﹣1|?2+?|t﹣1|?2=4，解得t=3或t=﹣1，
∴P点坐标为（0，3），（0，﹣1）；
（3）作EM∥AC，如图②，
∵AC∥BD，
∴AC∥EM∥BD，
∴∠CAE=∠AEM，∠BDE=∠DEM，
∴∠AED=∠CAE+∠BDE，
∵AE，DE分别平分∠CAB，∠ODB，
∴∠CAE=∠CAB，∠BDE=∠ODB，
∴∠AED=（∠CAB+∠ODB），
∵AC∥BD，
∴∠CAB=∠OBD，
∴∠CAB+∠ODB=∠OBD+∠ODB=90°，
∴∠AED=×90°=45°．