人教版八年级数学上册教学课件:11-3-2 多边形及其内角和 (共27张PPT)
文档属性
| 名称 | 人教版八年级数学上册教学课件:11-3-2 多边形及其内角和 (共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 497.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-15 00:00:00 | ||
图片预览

文档简介
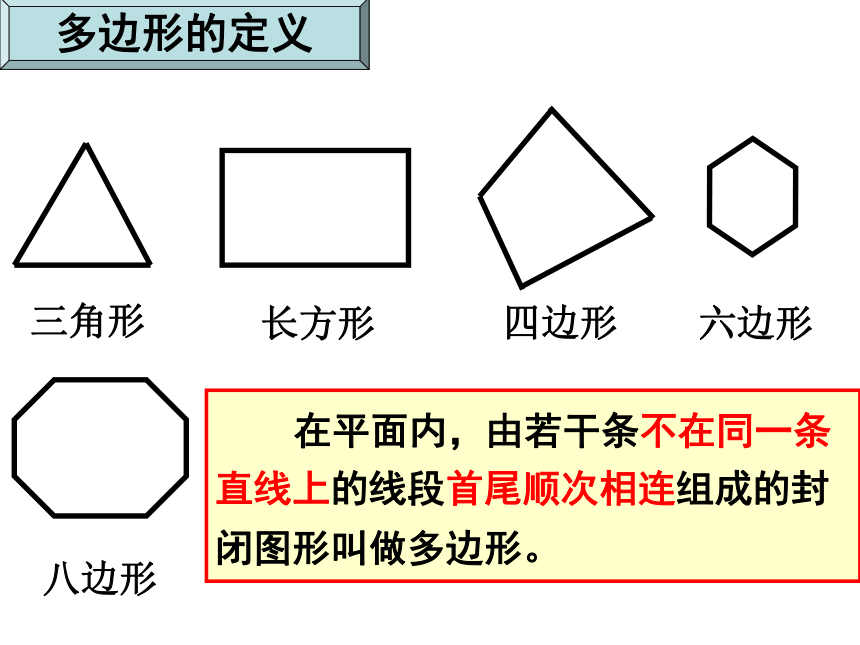
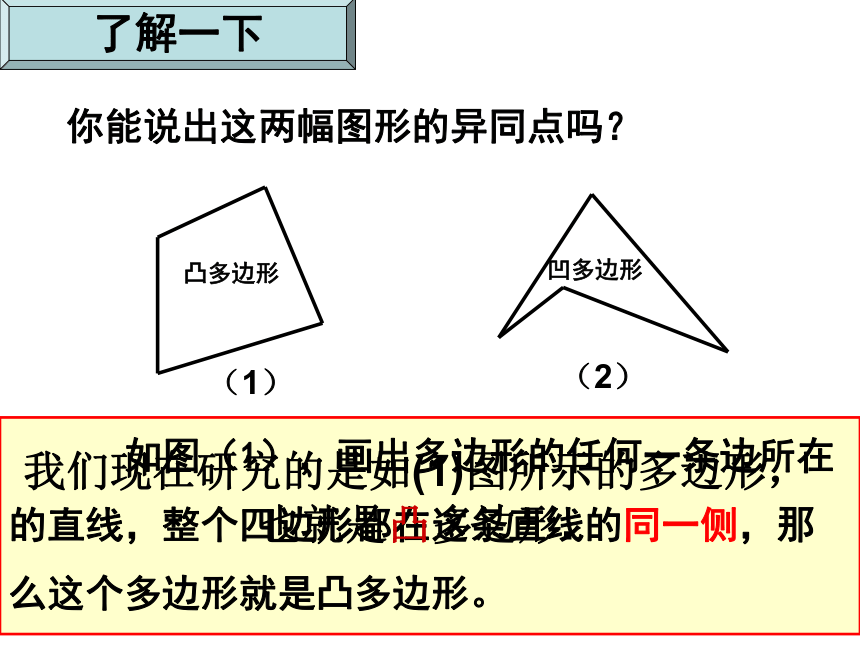
课件27张PPT。多边形及其内、外角和从这些图形你能抽象出什么平面图形? 走入生活 走入生活 走入生活 走入生活 在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。 多边形的定义 你能说出这两幅图形的异同点吗?(1)(2) 如图(1),画出多边形的任何一条边所在
的直线,整个四边形都在这条直线的同一侧,那
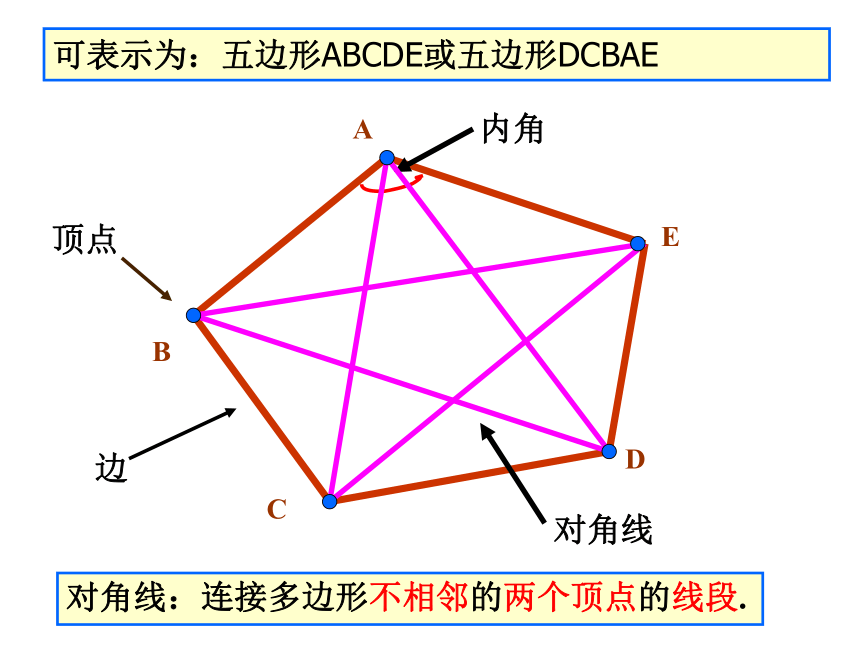
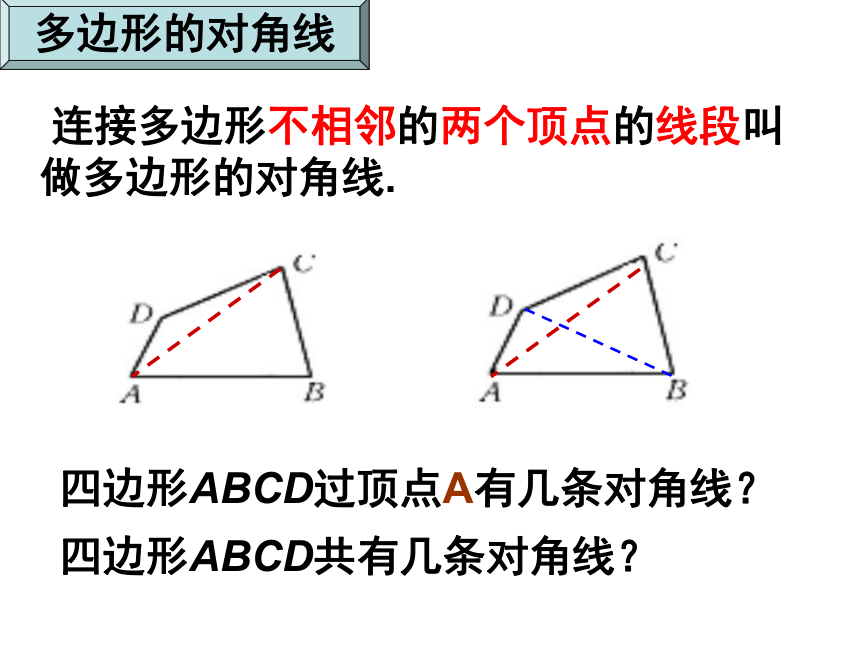
么这个多边形就是凸多边形。了解一下凸多边形凹多边形我们现在研究的是如(1)图所示的多边形,也就是凸多边形. 顶点内角边对角线对角线:连接多边形不相邻的两个顶点的线段.可表示为:五边形ABCDE或五边形DCBAEABCDE 连接多边形不相邻的两个顶点的线段叫做多边形的对角线. 四边形ABCD过顶点A有几条对角线?四边形ABCD共有几条对角线? 多边形的对角线 五边形ABCDE共有几条对角线呢?共有5条对角线六边形ABCDEF共有几条对角线呢?共有9条对角线有什么
规律呢?CDABE四边形从一个顶点出发,能引出__条对角线.五边形从一个顶点出发,能引出__条对角线.六边形从一个顶点出发,能引出__条对角线. n 边形从一个顶点出发,能引出___条对角线 ……123n-3共有2条.共有5条.共有9条.共有 条.探究 多边形的对角线 正三角形正四边形正五边形正六边形正八边形(正方形)(正三边形)(等边三角形) 正多边形如果多边形的各个角都相等,各条边也相等,那么这样的多边形叫做正多边形. 多边形的内角和 三角形内角和:180°四边形的内角和( 4-2)× 180°= 360° 四边形的内角和 (4-2)× 180°= 360° 五边形的内角和 (5-2)× 180°= 540° 六边形的内角和 (6-2)×180°= 720° 七边形的内角和(7-2)×180°= 900° n边形呢? 多边形的内角和 任意n边形内角和等于___________你还有其他的分割方法吗? (n -2)×180° 多边形的内角和 正五边形的内角和是____,正四边形的内角和是____,正六边形的内角和是_____,正八边形的内角和是_____,360°540°1080°正十边形的内角和是_____,1440°每个内角是____.每个内角是____.每个内角是____.每个内角是____.每个内角是____.正n边形的内角和是__________,每个内角是________.90°720°108°120°135°144°(n -2)×180°口答(2) 已知一个多边形每个内角都等108°, 求这个多边形的边数?解:(1) 设这个多边形的边数为 n,根据题意得: 答:这个多边形是11边形。例1: (1)如果一个多边形的内角和是1620°,那么它是几边形? (n-2) ×180=1620n-2 =9 解得:n=11 典例分析 (2) 已知一个多边形每个内角都等108°, 求这个多边形的边数?解:设这个多边形的边数为 n,根据题意得:答:这个多边形是五边形。(n-2) ×180=108 n
解得:n=5 课堂练习 1、求下列x的值. 书P24——练习1解:如图四边形ABCD中,例2:如果一个四边形的一组对角互补,那么另一组对角有什么关系?这就是说,如果四边形的一组对角互补,那么另一组对角也互补。设 典例分析 ABCD12345多边形的边与它的邻边的延长线组成的角. 外角 多边形的外角如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少? 多边形的外角和 思考:n边形的外角和为多少?
(n是不小于3的任意整数)多边形的外角和等于360°.从多边形的一个顶点A 出发,沿多边形的各边走过各顶点, 再回到点A, 然后转向出发时的方向.还可怎样理解多边形的外角和等于360°?ABCDEF在行程中所转的各个角的和, 就是多边形的外角和. 由于走了一周, 所转的各个角的和等于一个周角,所以多边形的外角和等于360°。 典例分析 1.一个正多边形的一个外角为40°,则
这个正多边形是________边形.2.一个正多边形的内角与外角和的比是4:1,则这个正多边形的边数为( )
A.8 B.9 C.10 D.12 九C1. 正五边形 的每一个外角等于___.每一个内角等于_____.72°108°3. 如果一个正多边形的一个内角等于150°,则这个多边形的边数是 ( )A. 12 B. 9 C. 8 D. 7A2. 如果一个多边形的每一个外角等于30°,则这个多边形的边数是____.12 课堂练习 提高练习 2.分别求出图(1)(2)(3)中,∠A+∠B+∠C+∠D+∠E+∠F的度数.
的直线,整个四边形都在这条直线的同一侧,那
么这个多边形就是凸多边形。了解一下凸多边形凹多边形我们现在研究的是如(1)图所示的多边形,也就是凸多边形. 顶点内角边对角线对角线:连接多边形不相邻的两个顶点的线段.可表示为:五边形ABCDE或五边形DCBAEABCDE 连接多边形不相邻的两个顶点的线段叫做多边形的对角线. 四边形ABCD过顶点A有几条对角线?四边形ABCD共有几条对角线? 多边形的对角线 五边形ABCDE共有几条对角线呢?共有5条对角线六边形ABCDEF共有几条对角线呢?共有9条对角线有什么
规律呢?CDABE四边形从一个顶点出发,能引出__条对角线.五边形从一个顶点出发,能引出__条对角线.六边形从一个顶点出发,能引出__条对角线. n 边形从一个顶点出发,能引出___条对角线 ……123n-3共有2条.共有5条.共有9条.共有 条.探究 多边形的对角线 正三角形正四边形正五边形正六边形正八边形(正方形)(正三边形)(等边三角形) 正多边形如果多边形的各个角都相等,各条边也相等,那么这样的多边形叫做正多边形. 多边形的内角和 三角形内角和:180°四边形的内角和( 4-2)× 180°= 360° 四边形的内角和 (4-2)× 180°= 360° 五边形的内角和 (5-2)× 180°= 540° 六边形的内角和 (6-2)×180°= 720° 七边形的内角和(7-2)×180°= 900° n边形呢? 多边形的内角和 任意n边形内角和等于___________你还有其他的分割方法吗? (n -2)×180° 多边形的内角和 正五边形的内角和是____,正四边形的内角和是____,正六边形的内角和是_____,正八边形的内角和是_____,360°540°1080°正十边形的内角和是_____,1440°每个内角是____.每个内角是____.每个内角是____.每个内角是____.每个内角是____.正n边形的内角和是__________,每个内角是________.90°720°108°120°135°144°(n -2)×180°口答(2) 已知一个多边形每个内角都等108°, 求这个多边形的边数?解:(1) 设这个多边形的边数为 n,根据题意得: 答:这个多边形是11边形。例1: (1)如果一个多边形的内角和是1620°,那么它是几边形? (n-2) ×180=1620n-2 =9 解得:n=11 典例分析 (2) 已知一个多边形每个内角都等108°, 求这个多边形的边数?解:设这个多边形的边数为 n,根据题意得:答:这个多边形是五边形。(n-2) ×180=108 n
解得:n=5 课堂练习 1、求下列x的值. 书P24——练习1解:如图四边形ABCD中,例2:如果一个四边形的一组对角互补,那么另一组对角有什么关系?这就是说,如果四边形的一组对角互补,那么另一组对角也互补。设 典例分析 ABCD12345多边形的边与它的邻边的延长线组成的角. 外角 多边形的外角如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和. 六边形的外角和等于多少? 多边形的外角和 思考:n边形的外角和为多少?
(n是不小于3的任意整数)多边形的外角和等于360°.从多边形的一个顶点A 出发,沿多边形的各边走过各顶点, 再回到点A, 然后转向出发时的方向.还可怎样理解多边形的外角和等于360°?ABCDEF在行程中所转的各个角的和, 就是多边形的外角和. 由于走了一周, 所转的各个角的和等于一个周角,所以多边形的外角和等于360°。 典例分析 1.一个正多边形的一个外角为40°,则
这个正多边形是________边形.2.一个正多边形的内角与外角和的比是4:1,则这个正多边形的边数为( )
A.8 B.9 C.10 D.12 九C1. 正五边形 的每一个外角等于___.每一个内角等于_____.72°108°3. 如果一个正多边形的一个内角等于150°,则这个多边形的边数是 ( )A. 12 B. 9 C. 8 D. 7A2. 如果一个多边形的每一个外角等于30°,则这个多边形的边数是____.12 课堂练习 提高练习 2.分别求出图(1)(2)(3)中,∠A+∠B+∠C+∠D+∠E+∠F的度数.
