人教版数学选修2-2:1.3.1 函数的单调性与导数 教学设计
文档属性
| 名称 | 人教版数学选修2-2:1.3.1 函数的单调性与导数 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 25.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-15 21:53:17 | ||
图片预览

文档简介
第一课时
函数的单调性与导数
(一)课堂设计理念
先以具体问题引入,让学生意识到用定义法、图象法在处理一些单调性问题时难度之大,激发学生的学习兴趣,再让学生数形结合,通过观察分析、小组讨论的方式得出函数单调性与导数之间的联系。
课堂设计意图
建立函数单调性与导数之间的联系是本节课的关键。课堂中先以具体问题引入,让学生意识到在处理一些单调性问题时定义法、图象法的不便,激发学生的求知欲;接下来让学生数形结合,通过小组讨论的方式得出函数单调性与导数间的联系,这样既有助于活跃课堂气氛又加深了学生对结论的理解。在练习上,紧扣高考题,并采用小组竞赛的方式,有效地调动了学生的积极性。
教材分析
本节的教学内容属导数的应用,是在学生学习了导数的概念、计算、几何意义的基础上学习的内容,学好它既可加深对导数的理解,又可为后面研究函数的极值和最值打好基础。由于学生在高一已经掌握了单调性的定义,并能用定义判定在给定区间上函数的单调性。通过本节课的学习,应使学生体验到,用导数判断单调性要比用定义判断简捷得多(尤其对于三次和三次以上的多项式函数,或图象难以画出的函数而言),充分展示了导数解决问题的优越性。
高考要求:了解函数导数与单调性的关系,能利用导数研究函数单调性,会求函数单调区间。这部分在高考中几乎每年都有涉及,所占分值比重较大
(四)教学目标
知识目标:能探索并应用函数的单调性与导数的关系求单调区间,能由导数信息绘制函数大致图象。
能力目标:培养学生的观察能力、归纳能力,增强数形结合的思维意识。
情感目标:通过在教学过程中让学生多动手、多观察、勤思考、善总结,引导学生养成自主学习的学习习惯。
(五)教学重点、难点
重点:探索并应用函数单调性与导数的关系求单调区间。
难点:利用导数信息绘制函数的大致图象。
学生情况分析
有利因素:
1)已经学习了函数的单调性,会用图像法、定义法求函数的单调性;
2)在物理学瞬时速度的辅助下掌握了导数概念及几何意义,会求简单函数的导函数;
3)学生好奇心强,探究导数与函数单调性关系对他们而言是一个挑战,更能激发他们学习兴趣。
不利因素:学生发现能力欠缺,对于这两个知识板块的整合,学生存在很大兴趣,但却容易无从下手,所以本节课教师要注意引导学生数形结合去发现规律,总结结论。
教学方法、教学策略选择与设计
1、教学方法的选择:本节课以“问题解决”贯穿始终,采用发现式、启发式的教学方法。通过问题激发学生求知欲,使学生主动参与教学实践活动,在教师的指导下发现、分析和解决问题,总结规律,培养积极探索的科学精神.
2、教学手段的利用:
本节课采用多媒体课件等辅助手段以加大课堂容量,通过数形结合,使抽象的知识直观化,形象化,以促进学生的理解.
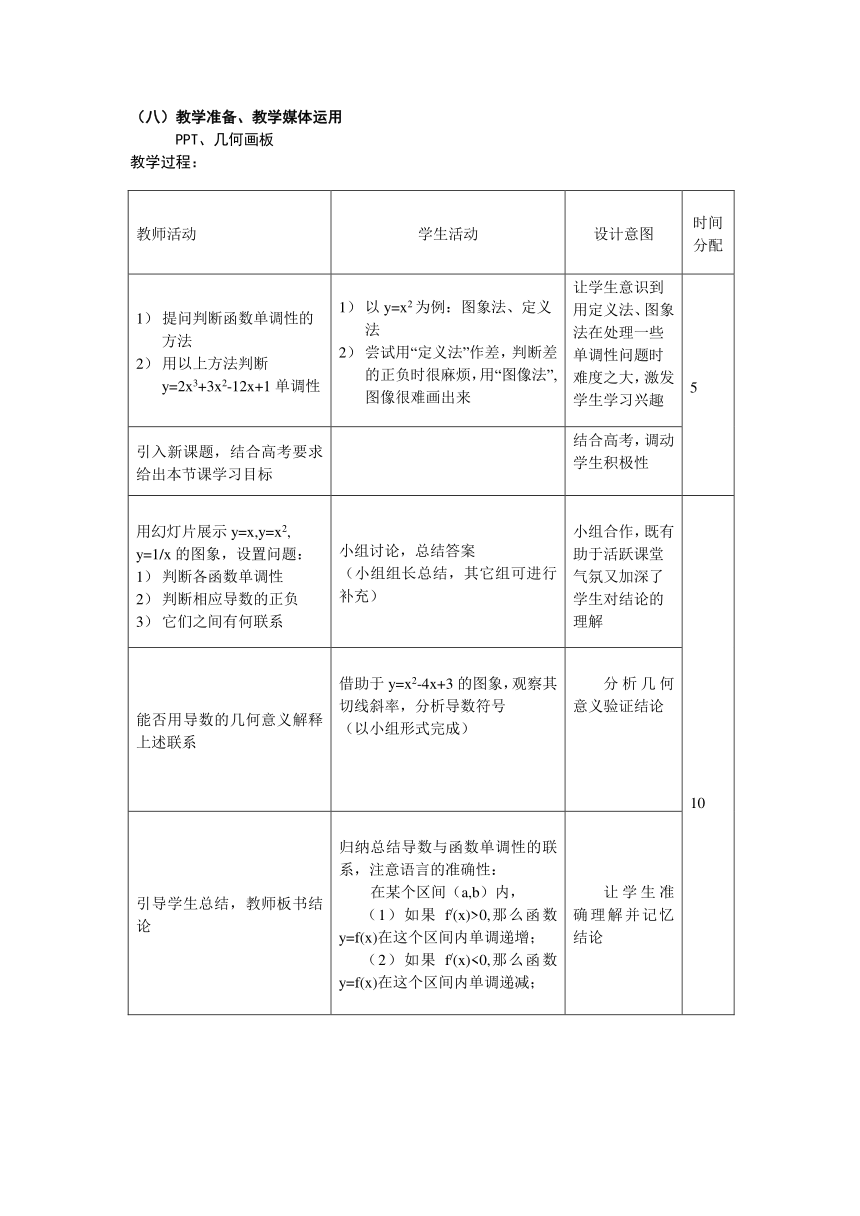
(八)教学准备、教学媒体运用
PPT、几何画板
教学过程:
教师活动
学生活动
设计意图
时间分配
提问判断函数单调性的方法用以上方法判断y=2x3+3x2-12x+1单调性
以y=x2为例:图象法、定义法尝试用“定义法”作差,判断差的正负时很麻烦,用“图像法”,图像很难画出来
让学生意识到用定义法、图象法在处理一些单调性问题时难度之大,激发学生学习兴趣
5
引入新课题,结合高考要求给出本节课学习目标
结合高考,调动学生积极性
用幻灯片展示y=x,y=x2,y=1/x的图象,设置问题:判断各函数单调性判断相应导数的正负它们之间有何联系
小组讨论,总结答案(小组组长总结,其它组可进行补充)
小组合作,既有助于活跃课堂气氛又加深了学生对结论的理解
10
能否用导数的几何意义解释上述联系
借助于y=x2-4x+3的图象,观察其切线斜率,分析导数符号(以小组形式完成)
分析几何意义验证结论
引导学生总结,教师板书结论
归纳总结导数与函数单调性的联系,注意语言的准确性:在某个区间(a,b)内,(1)如果f/(x)>0,那么函数y=f(x)在这个区间内单调递增;(2)如果f/(x)<0,那么函数y=f(x)在这个区间内单调递减;
让学生准确理解并记忆结论
设置问题:1)、若y=lnx,试求y的导数及单调区间。强调:应正确理解“某个区间”的含义,它必是定义域内的某个区间。2)、如果在某个区间内恒有f/(x)=0,函数f(x)有什么特性?
1)y/=1/x,单调递增区间为(0,+∞)(有些学生会直接根据导数的正负错误地得到两个单调区间)2)
常函数
通过问题让学生纠正易错点,加深对结论的理解
.例1:已知导函数y=f(x)具备下列信息:①当10;②当x>4或x<1时,f’(x)<0
③当x=4或x=1时,f’(x)=0,
试画出函数的大致图象
学生小组讨论,然后板书答案。
会结合导数正负判断原函数图象
5
巩固练习:(高考原题)根据导数图象选择原函数图象
自由发言,阐述依据
例2.判断y=2x3+3x2-12x+1的单调性并求其单调区间巩固练习:判断下列函数的单调性,并求出单调区间:1).f(x)=sinx-x
x∈(0,)2)f(x)=2x3+3x2-24x+1教师通过几何画板展示图象,验证答案
1)学生口述,教师板书步骤注意:若函数的单调区间有多个,应用逗号隔开,不能用并集表示。2)归纳步骤:(1)确定函数定义域;(2)求f
'(x);(3)解不等式f
'(x)>0(或f
'(x)<0)(4)下结论,指出单调区间学生板书步骤
通过练习,掌握用导数求单调区间的步骤巩固强化
55
变式训练:
求证f(x)=2x3-6x2+7在(0,2)内是减函数
小组讨论,口述步骤
灵活运用导数处理单调性问题
5
课堂小结:(由学生完成)本节课我们学习到了哪些内容?如何利用导数来求单调区间
随堂检测:(高考原题)1.(浙江理工类)已知函数图象选导数图象2.(全国理)函数y=xcosx-sinx在下列哪个区间内是增函数?A
BC
D
学生自主完成DB
巩固知识,查缺补漏。
5
作业布置
复习本节课内容,理清脉络;2.
阳光课堂《函数的单调性与导数》练习
板书设计
函数的单调性与导数
1.结论
2.求单调区间步骤
3.例题
教学反思:本节课通过观察分析、小组讨论,加深了学生对函数单调性与导数关系的理解,但在练习中发现部分学生对求导公式记忆不牢,运用时不熟练且易出错,所以接下来的学习中还要加强此方面的巩固练习。
A
B
x
y
o
2
3
函数的单调性与导数
(一)课堂设计理念
先以具体问题引入,让学生意识到用定义法、图象法在处理一些单调性问题时难度之大,激发学生的学习兴趣,再让学生数形结合,通过观察分析、小组讨论的方式得出函数单调性与导数之间的联系。
课堂设计意图
建立函数单调性与导数之间的联系是本节课的关键。课堂中先以具体问题引入,让学生意识到在处理一些单调性问题时定义法、图象法的不便,激发学生的求知欲;接下来让学生数形结合,通过小组讨论的方式得出函数单调性与导数间的联系,这样既有助于活跃课堂气氛又加深了学生对结论的理解。在练习上,紧扣高考题,并采用小组竞赛的方式,有效地调动了学生的积极性。
教材分析
本节的教学内容属导数的应用,是在学生学习了导数的概念、计算、几何意义的基础上学习的内容,学好它既可加深对导数的理解,又可为后面研究函数的极值和最值打好基础。由于学生在高一已经掌握了单调性的定义,并能用定义判定在给定区间上函数的单调性。通过本节课的学习,应使学生体验到,用导数判断单调性要比用定义判断简捷得多(尤其对于三次和三次以上的多项式函数,或图象难以画出的函数而言),充分展示了导数解决问题的优越性。
高考要求:了解函数导数与单调性的关系,能利用导数研究函数单调性,会求函数单调区间。这部分在高考中几乎每年都有涉及,所占分值比重较大
(四)教学目标
知识目标:能探索并应用函数的单调性与导数的关系求单调区间,能由导数信息绘制函数大致图象。
能力目标:培养学生的观察能力、归纳能力,增强数形结合的思维意识。
情感目标:通过在教学过程中让学生多动手、多观察、勤思考、善总结,引导学生养成自主学习的学习习惯。
(五)教学重点、难点
重点:探索并应用函数单调性与导数的关系求单调区间。
难点:利用导数信息绘制函数的大致图象。
学生情况分析
有利因素:
1)已经学习了函数的单调性,会用图像法、定义法求函数的单调性;
2)在物理学瞬时速度的辅助下掌握了导数概念及几何意义,会求简单函数的导函数;
3)学生好奇心强,探究导数与函数单调性关系对他们而言是一个挑战,更能激发他们学习兴趣。
不利因素:学生发现能力欠缺,对于这两个知识板块的整合,学生存在很大兴趣,但却容易无从下手,所以本节课教师要注意引导学生数形结合去发现规律,总结结论。
教学方法、教学策略选择与设计
1、教学方法的选择:本节课以“问题解决”贯穿始终,采用发现式、启发式的教学方法。通过问题激发学生求知欲,使学生主动参与教学实践活动,在教师的指导下发现、分析和解决问题,总结规律,培养积极探索的科学精神.
2、教学手段的利用:
本节课采用多媒体课件等辅助手段以加大课堂容量,通过数形结合,使抽象的知识直观化,形象化,以促进学生的理解.
(八)教学准备、教学媒体运用
PPT、几何画板
教学过程:
教师活动
学生活动
设计意图
时间分配
提问判断函数单调性的方法用以上方法判断y=2x3+3x2-12x+1单调性
以y=x2为例:图象法、定义法尝试用“定义法”作差,判断差的正负时很麻烦,用“图像法”,图像很难画出来
让学生意识到用定义法、图象法在处理一些单调性问题时难度之大,激发学生学习兴趣
5
引入新课题,结合高考要求给出本节课学习目标
结合高考,调动学生积极性
用幻灯片展示y=x,y=x2,y=1/x的图象,设置问题:判断各函数单调性判断相应导数的正负它们之间有何联系
小组讨论,总结答案(小组组长总结,其它组可进行补充)
小组合作,既有助于活跃课堂气氛又加深了学生对结论的理解
10
能否用导数的几何意义解释上述联系
借助于y=x2-4x+3的图象,观察其切线斜率,分析导数符号(以小组形式完成)
分析几何意义验证结论
引导学生总结,教师板书结论
归纳总结导数与函数单调性的联系,注意语言的准确性:在某个区间(a,b)内,(1)如果f/(x)>0,那么函数y=f(x)在这个区间内单调递增;(2)如果f/(x)<0,那么函数y=f(x)在这个区间内单调递减;
让学生准确理解并记忆结论
设置问题:1)、若y=lnx,试求y的导数及单调区间。强调:应正确理解“某个区间”的含义,它必是定义域内的某个区间。2)、如果在某个区间内恒有f/(x)=0,函数f(x)有什么特性?
1)y/=1/x,单调递增区间为(0,+∞)(有些学生会直接根据导数的正负错误地得到两个单调区间)2)
常函数
通过问题让学生纠正易错点,加深对结论的理解
.例1:已知导函数y=f(x)具备下列信息:①当1
③当x=4或x=1时,f’(x)=0,
试画出函数的大致图象
学生小组讨论,然后板书答案。
会结合导数正负判断原函数图象
5
巩固练习:(高考原题)根据导数图象选择原函数图象
自由发言,阐述依据
例2.判断y=2x3+3x2-12x+1的单调性并求其单调区间巩固练习:判断下列函数的单调性,并求出单调区间:1).f(x)=sinx-x
x∈(0,)2)f(x)=2x3+3x2-24x+1教师通过几何画板展示图象,验证答案
1)学生口述,教师板书步骤注意:若函数的单调区间有多个,应用逗号隔开,不能用并集表示。2)归纳步骤:(1)确定函数定义域;(2)求f
'(x);(3)解不等式f
'(x)>0(或f
'(x)<0)(4)下结论,指出单调区间学生板书步骤
通过练习,掌握用导数求单调区间的步骤巩固强化
55
变式训练:
求证f(x)=2x3-6x2+7在(0,2)内是减函数
小组讨论,口述步骤
灵活运用导数处理单调性问题
5
课堂小结:(由学生完成)本节课我们学习到了哪些内容?如何利用导数来求单调区间
随堂检测:(高考原题)1.(浙江理工类)已知函数图象选导数图象2.(全国理)函数y=xcosx-sinx在下列哪个区间内是增函数?A
BC
D
学生自主完成DB
巩固知识,查缺补漏。
5
作业布置
复习本节课内容,理清脉络;2.
阳光课堂《函数的单调性与导数》练习
板书设计
函数的单调性与导数
1.结论
2.求单调区间步骤
3.例题
教学反思:本节课通过观察分析、小组讨论,加深了学生对函数单调性与导数关系的理解,但在练习中发现部分学生对求导公式记忆不牢,运用时不熟练且易出错,所以接下来的学习中还要加强此方面的巩固练习。
A
B
x
y
o
2
3
