湖南省株洲五中2015-2016学年高二(下)入学数学试卷(理科)(解析版)
文档属性
| 名称 | 湖南省株洲五中2015-2016学年高二(下)入学数学试卷(理科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 248.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-16 15:26:36 | ||
图片预览




文档简介
2015-2016学年湖南省株洲五中高二(下)入学数学试卷(理科)
一、选择题(每小题5分,共60分)
1.已知复数z=﹣i+2,则z的虚部为( )
A.i
B.﹣1
C.1
D.﹣i
2.已知a,b,c,d为实数,且c>d,则“a>b”是“a+c>b+d”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
3.下列函数求导运算正确的个数为( )
①(3x)′=3xlog3e;
②(log2x)′=
③(ex)′=ex;
④()′=x;
⑤(x ex)′=ex+1.
A.1
B.2
C.3
D.4
4.已知A、B、C三点不共线,O是平面ABC外的任一点,下列条件中能确定点M与点A、B、C一定共面的是( )
A.
B.
C.
D.
5.(1)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.
(2)“x=1”是“x2﹣4x+3=0”的充要条件;
(3)若p∧q为假命题,则p、q均为假命题.
(4)对于命题p: x0∈R,x+2x0+2≤0,则¬p: x∈R,x2+2x+2>0.
上面四个命题中正确的个数是( )
A.1
B.2
C.3
D.4
6.在△ABC中,角A、B、C所对的边长分别为a,b,c,若A=60°,B=45°,,则b=( )
A.
B.2
C.
D.
7.抛物线y2+4x=0上的点P到直线x=2的距离等于4,则P到焦点F的距离|PF|=( )
A.1
B.2
C.3
D.4
8.在正三棱柱ABC﹣A1B1C1中,已知AB=2,CC1=,则异面直线AB1和BC1所成角的余弦值为( )
A.0
B.
C.
D.
9.等比数列{an}中,a4=2,a5=5,则数列{lgan}的前8项和等于( )
A.6
B.5
C.4
D.3
10.双曲线C:﹣=1(a>0,b>0)的右焦点为F,若以点F为圆心,半径为a的圆与双曲线C的渐近线相切,则双曲线C的离心率等于( )
A.
B.
C.2
D.2
11.如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为(n≥2),并且相邻两行数之间有一定的关系,则第7行第4个数(从左往右数)为( )
A.
B.
C.
D.
12.若函数f(x)=+2x(a>0,b≥0)在区间[1,2]上单调递减,则a(b﹣1)的最大值为( )
A.4
B.
C.
D.
二、填空题(每小题5分,共20分)
13.(理)______.
14.函数f(x)=x3﹣3x2+1在x=______处取得极小值.
15.若实x,y满足不等式组目标函t=x﹣2y的最大值为2,则实a的值是______.
16.已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=2且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为______.
三、解答题(共70分)
17.已知m∈R,设命题p:方程+=1表示焦点在y轴上的椭圆;命题q:函数f(x)=3x2+2mx+m+有零点.
(1)若¬p为真命题,求m的取值范围;
(2)若“p∨q”为真,求m的取值范围.
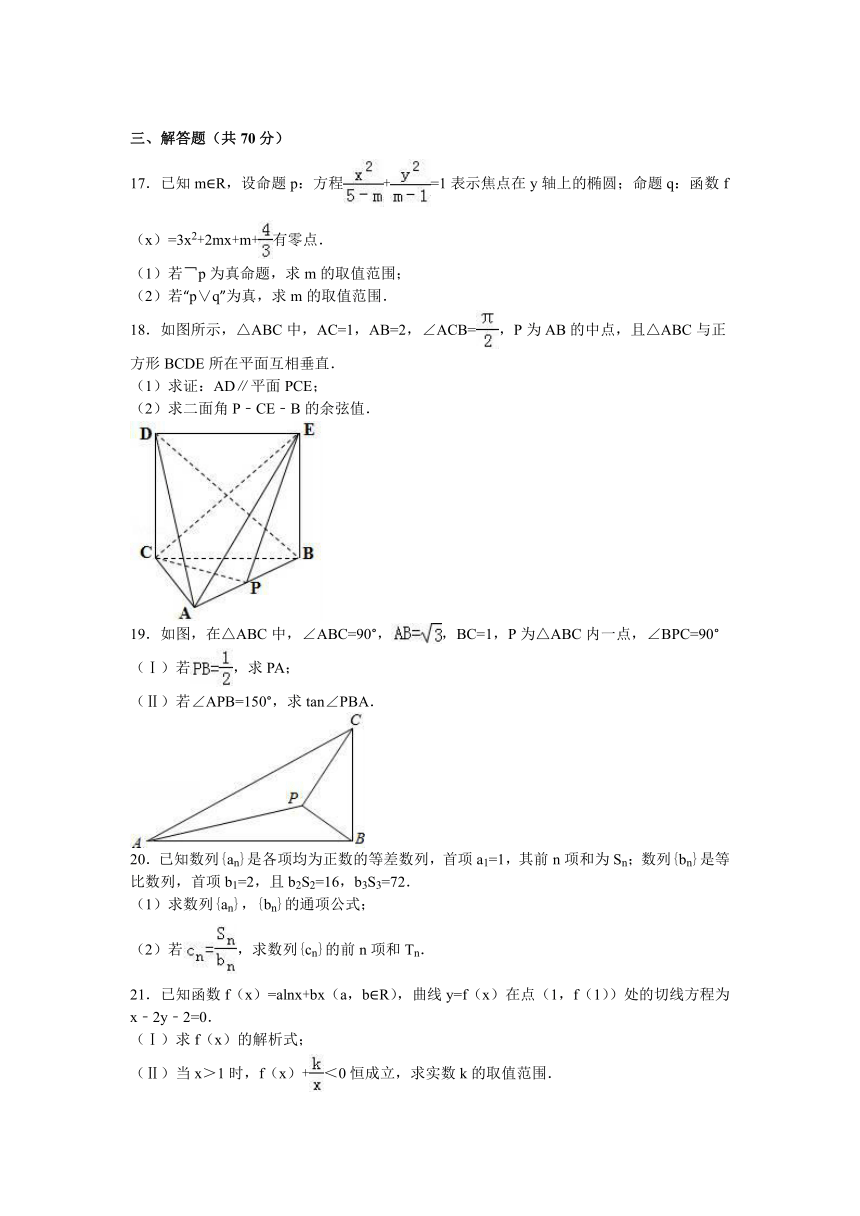
18.如图所示,△ABC中,AC=1,AB=2,∠ACB=,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
(1)求证:AD∥平面PCE;
(2)求二面角P﹣CE﹣B的余弦值.
19.如图,在△ABC中,∠ABC=90°,,BC=1,P为△ABC内一点,∠BPC=90°
(Ⅰ)若,求PA;
(Ⅱ)若∠APB=150°,求tan∠PBA.
20.已知数列{an}是各项均为正数的等差数列,首项a1=1,其前n项和为Sn;数列{bn}是等比数列,首项b1=2,且b2S2=16,b3S3=72.
(1)求数列{an},{bn}的通项公式;
(2)若,求数列{cn}的前n项和Tn.
21.已知函数f(x)=alnx+bx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为x﹣2y﹣2=0.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x>1时,f(x)+<0恒成立,求实数k的取值范围.
22.设椭圆C:
=1的左右焦点分别为F1,F2,直线y=x﹣1过椭圆的焦点F2且与椭圆交于P,Q两点,若△F1PQ周长为4.
(1)求椭圆的方程;
(2)圆C′:x2+y2=1,直线y=kx+m与圆C′相切且与椭圆C交于不同的两点A,B,O为坐标原点.若 =λ,且≤λ≤,求△OAB的取值范围.
2015-2016学年湖南省株洲五中高二(下)入学数学试卷(理科)
参考答案与试题解析
一、选择题(每小题5分,共60分)
1.已知复数z=﹣i+2,则z的虚部为( )
A.i
B.﹣1
C.1
D.﹣i
【考点】复数的基本概念.
【分析】直接利用复数的概念写出结果即可.
【解答】解:复数z=﹣i+2,则z的虚部为:﹣1.
故选:B.
2.已知a,b,c,d为实数,且c>d,则“a>b”是“a+c>b+d”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据不等式的性质,结合充分条件和必要条件的定义进行判断即可.
【解答】解:若a>b,∵c>d,∴a+c>b+d成立.
当c=3,d=2,a=b=0时,满足a+c>b+d,但a>b不成立.
故“a>b”是“a+c>b+d”的充分不必要条件.
故选:A.
3.下列函数求导运算正确的个数为( )
①(3x)′=3xlog3e;
②(log2x)′=
③(ex)′=ex;
④()′=x;
⑤(x ex)′=ex+1.
A.1
B.2
C.3
D.4
【考点】导数的运算.
【分析】根据(ax)′=axlna,(logax)′=,(lnx)'=即可作出判断.
【解答】解:①(3x)′=3xln3,故错误;
②(log2x)′=,故正确;
③(ex)'=ex,故正确;
④()′=﹣,故错误;
⑤(x ex)′=ex+x ex,故错误.
故选:B.
4.已知A、B、C三点不共线,O是平面ABC外的任一点,下列条件中能确定点M与点A、B、C一定共面的是( )
A.
B.
C.
D.
【考点】共线向量与共面向量.
【分析】根据共面向量定理,说明M、A、B、C共面,判断选项的正误.
【解答】解:由共面向量定理,
说明M、A、B、C共面,
可以判断A、B、C都是错误的,
则D正确.
故选D.
5.(1)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.
(2)“x=1”是“x2﹣4x+3=0”的充要条件;
(3)若p∧q为假命题,则p、q均为假命题.
(4)对于命题p: x0∈R,x+2x0+2≤0,则¬p: x∈R,x2+2x+2>0.
上面四个命题中正确的个数是( )
A.1
B.2
C.3
D.4
【考点】命题的真假判断与应用.
【分析】(1)根据逆否命题的定义进行判断,
(2)根据充分条件和必要条件的定义进行判断即可
(3)根据复合命题真假之间的关系进行判断
(4)根据特称命题的否定是全称命题进行判断即可.
【解答】解:(1)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.正确,
(2)由x2﹣4x+3=0得x=1或x=3,则“x=1”是“x2﹣4x+3=0”的充分不必要条件;故(2)错误,
(3)若p∧q为假命题,则p、q至少有一个为假命题.故(3)错误,
(4)对于命题p: x0∈R,x+2x0+2≤0,则¬p: x∈R,x2+2x+2>0.正确,
故正确的是(1)(4),
故选:B.
6.在△ABC中,角A、B、C所对的边长分别为a,b,c,若A=60°,B=45°,,则b=( )
A.
B.2
C.
D.
【考点】正弦定理.
【分析】由正弦定理的式子,结合题中数据加以计算,可得b==2.
【解答】解:∵△ABC中,A=60°,B=45°,,
∴由正弦定理,得b===2.
故选:B
7.抛物线y2+4x=0上的点P到直线x=2的距离等于4,则P到焦点F的距离|PF|=( )
A.1
B.2
C.3
D.4
【考点】抛物线的简单性质.
【分析】由抛物线的方程求出其焦点坐标和准线方程,利用已知求得P到准线的距离,则答案可求.
【解答】解:由y2+4x=0,得y2=﹣4x,
∴抛物线的焦点F(﹣1,0),准线方程为x=1.
如图:
∵P到直线x=2的距离为4,∴P到准线x=1的距离为3,
则P到焦点F的距离|PF|=3.
故选:C.
8.在正三棱柱ABC﹣A1B1C1中,已知AB=2,CC1=,则异面直线AB1和BC1所成角的余弦值为( )
A.0
B.
C.
D.
【考点】异面直线及其所成的角.
【分析】连接B1C交BC1于E,连接DE,利用四边形BCC1B1是平行四边形及其三角形的中位线定理证明DE∥AB1,可得∠DEB或其补角为异面直线AB1与BC1所成的角,再利用余弦定理即可得出.
【解答】解:如图所示
连接B1C交BC1于E,连接DE,
∵四边形BCC1B1是平行四边形,∴B1E=EC.
又AD=DC.
∴DE∥AB1,
∴∠DEB或其补角为异面直线AB1与BC1所成的角,
在△DEB中,DE=,BD=,BE=.
∴cos∠DEB==0,
∴异面直线AB1和BC1所成角的余弦值为0.
故选:A.
9.等比数列{an}中,a4=2,a5=5,则数列{lgan}的前8项和等于( )
A.6
B.5
C.4
D.3
【考点】等比数列的前n项和.
【分析】利用等比数列的性质可得a1a8=a2a7=a3a6=a4a5=10.再利用对数的运算性质即可得出.
【解答】解:∵数列{an}是等比数列,a4=2,a5=5,
∴a1a8=a2a7=a3a6=a4a5=10.
∴lga1+lga2+…+lga8
=lg(a1a2 … a8)
=
4lg10
=4.
故选:C.
10.双曲线C:﹣=1(a>0,b>0)的右焦点为F,若以点F为圆心,半径为a的圆与双曲线C的渐近线相切,则双曲线C的离心率等于( )
A.
B.
C.2
D.2
【考点】双曲线的简单性质.
【分析】根据双曲线方程表示出F坐标,以及渐近线方程,由以点F为圆心,半径为a的圆与双曲线C的渐近线相切,得到圆心F到渐近线距离d=r,整理得到a=b,再利用双曲线的简单性质及离心率公式计算即可.
【解答】解:根据题意得:圆心F(c,0),半径为a,双曲线渐近线方程为y=±x,即±bx﹣ay=0,
∵以点F为圆心,半径为a的圆与双曲线C的渐近线相切,且c2=a2+b2,
∴圆心F到渐近线的距离d==a,即a=b,
∴c====a,
则双曲线C的离心率e==,
故选:B.
11.如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为(n≥2),并且相邻两行数之间有一定的关系,则第7行第4个数(从左往右数)为( )
A.
B.
C.
D.
【考点】归纳推理.
【分析】根据每个数是它下一行左右相邻两数的和,先求出第5,6,7三行的第2个数,再求出6,7两行的第3个数,求出第7行的第4个数.
【解答】解:设第n行第m个数为a(n,m),
由题意知a(6,1)=,a(7,1)=,
∴a(7,2)=a(6,1)﹣a(7,1)=﹣=,
a(6,2)=a(5,1)﹣a(6,1)=﹣=,
a(7,3)=a(6,2)﹣a(7,2)=﹣=,
a(6,3)=a(5,2)﹣a(6,2)=﹣=,
∴a(7,4)=a(6,3)﹣a(7,3)=﹣=.
故选A.
12.若函数f(x)=+2x(a>0,b≥0)在区间[1,2]上单调递减,则a(b﹣1)的最大值为( )
A.4
B.
C.
D.
【考点】利用导数研究函数的单调性;基本不等式.
【分析】求得f(x)的导数,由题意可得f′(x)≤0在区间[1,2]上恒成立,可得,作出不等式组在第四象限的可行域,再由目标函数表示的双曲线,结合直线与双曲线相切,求得导数,设出切点,解方程可得切点,进而得到所求最大值.
【解答】解:函数f(x)=ax3+(b﹣8)x2+2x(a>0,b≥0),
f′(x)=ax2+(b﹣8)x+2,
由题意可得f′(x)≤0在区间[1,2]上恒成立,
即有,即为,(
)
以(a,b)为坐标,作出不等式组(
)在第一象限的可行域,如图:
,
令t=a(b﹣1),可得b=+1,此函数的图象为双曲线,
当直线b=7﹣2a与双曲线b=+1相切时,t取得最大值,
由得:2a2﹣6a+t=0,
△=36﹣8t=0,
解得t=,
故选:C.
二、填空题(每小题5分,共20分)
13.(理) π+2 .
【考点】定积分.
【分析】根据定积分的定义,找出三角函数的原函数然后代入计算即可.
【解答】解:(x+sinx)=+1﹣(﹣1)=π+2,
故答案为π+2.
14.函数f(x)=x3﹣3x2+1在x= 2 处取得极小值.
【考点】利用导数研究函数的极值.
【分析】首先求导可得f′(x)=3x2﹣6x,解3x2﹣6x=0可得其根,再判断导函数的符号即可.
【解答】解:f′(x)=3x2﹣6x,
令f′(x)=3x2﹣6x=0得x1=0,x2=2,
且x∈(﹣∞,0)时,f′(x)>0;x∈(0,2)时,f′(x)<0;x∈(2,+∞)时,f′(x)>0,
故f(x)在x=2出取得极小值.
故答案为:2.
15.若实x,y满足不等式组目标函t=x﹣2y的最大值为2,则实a的值是 2 .
【考点】简单线性规划.
【分析】画出约束条件表示的可行域,然后根据目标函数t=x﹣2y的最大值为2,确定约束条件中a值.
【解答】解:由题意约束条件的可行域是图中的阴影部分,
目标函数t=x﹣2y的最大值为2,
就是直线t=x﹣2y,经过直线x=2与直线x+2y﹣a=0的交点,
也就是x=2与x﹣2y=2的交点A(2,0),
所以a=x+2y=2+2×0=2,
则实a的值是2,
故答案为:2.
16.已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=2且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为 .
【考点】余弦定理;正弦定理.
【分析】由正弦定理化简已知可得2a﹣b2=c2﹣bc,结合余弦定理可求A的值,由基本不等式可求bc≤4,再利用三角形面积公式即可计算得解.
【解答】解:因为:(2+b)(sinA﹣sinB)=(c﹣b)sinC
(2+b)(a﹣b)=(c﹣b)c
2a﹣b2=c2﹣bc,
又因为:a=2,
所以:,
△ABC面积,
而b2+c2﹣a2=bc
b2+c2﹣bc=a2
b2+c2﹣bc=4
bc≤4
所以:,即△ABC面积的最大值为.
故答案为:.
三、解答题(共70分)
17.已知m∈R,设命题p:方程+=1表示焦点在y轴上的椭圆;命题q:函数f(x)=3x2+2mx+m+有零点.
(1)若¬p为真命题,求m的取值范围;
(2)若“p∨q”为真,求m的取值范围.
【考点】复合命题的真假.
【分析】(1)p:m﹣1>5﹣m>0,解出m范围,由于 p为真命题,可得p为假命题,即可得出.
(2)函数有零点,可得△≥0,由于“p∨q”为真,可得m∈P∪Q.
【解答】解:(1)p:m﹣1>5﹣m>0,∴3<m<5,…
∵ p为真命题,∴p为假命题…
∴m≤3或m≥5.…
(2)函数有零点,∴△≥0,≥0,…
∴m≥4或m≤﹣1.…
设Q={m|m≥4或m≤﹣1},P={m|3<m<5}.
∵“p∨q”为真,∴m∈P∪Q,即m>3或m≤﹣1.…
18.如图所示,△ABC中,AC=1,AB=2,∠ACB=,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
(1)求证:AD∥平面PCE;
(2)求二面角P﹣CE﹣B的余弦值.
【考点】二面角的平面角及求法;直线与平面平行的判定.
【分析】(Ⅰ)设BD∩CE=0,连结OP,则OP∥AD,由此能证明AD∥平面PCE;
(2)以C为原点,CA为x轴,CB为y轴,CD为z轴,建立空间直角坐标系,利用向量法能求出二面角P﹣CE﹣B的余弦值.
【解答】解:(1)证明:设BD∩CE=0,连结OP,
∵正方形BCDE对角线互相平分,∴O是BD中点,
∵P为AB的中点,∴OP∥AD,
∵AD 平面PCE,OP 平面PCE,
∴AD∥平面PCE;
(2)∵△ABC中,AC=1,AB=2,∠ACB=,
P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直,
∴CD⊥平面ABC,
以C为原点,CA为x轴,CB为y轴,CD为z轴,
建立空间直角坐标系,
C(0,0,0),A(1,0,0),B(0,2,0),
P(),E(0,2,2),
=(),=(0,2,2),
设平面PCE的法向量=(x,y,z),
则,取x=2,得=(2,﹣2,2),
平面BCE的法向量=(1,0,0),
设二面角P﹣CE﹣B的平面角为θ,
则cosθ===.
∴二面角P﹣CE﹣B的余弦值为.
19.如图,在△ABC中,∠ABC=90°,,BC=1,P为△ABC内一点,∠BPC=90°
(Ⅰ)若,求PA;
(Ⅱ)若∠APB=150°,求tan∠PBA.
【考点】余弦定理;正弦定理.
【分析】(I)在Rt△PBC,利用边角关系即可得到∠PBC=60°,得到∠PBA=30°.在△PBA中,利用余弦定理即可求得PA.
(II)设∠PBA=α,在Rt△PBC中,可得PB=sinα.在△PBA中,由正弦定理得,即,化简即可求出.
【解答】解:(I)在Rt△PBC中,
=,∴∠PBC=60°,∴∠PBA=30°.
在△PBA中,由余弦定理得PA2=PB2+AB2﹣2PB ABcos30°==.
∴PA=.
(II)设∠PBA=α,在Rt△PBC中,PB=BCcos(90°﹣α)=sinα.
在△PBA中,由正弦定理得,即,
化为.∴.
20.已知数列{an}是各项均为正数的等差数列,首项a1=1,其前n项和为Sn;数列{bn}是等比数列,首项b1=2,且b2S2=16,b3S3=72.
(1)求数列{an},{bn}的通项公式;
(2)若,求数列{cn}的前n项和Tn.
【考点】数列的求和.
【分析】(1)由已知条件,利用等差数列、等比数列的通项公式、前n项和列出方程组,求出等差数列的公差和等比数列的公比,由此能求出an与bn;
(2)由(1)能推导出Sn=n2,两次运用数列的求和方法:错位相减法,结合等比数列的求和公式.
【解答】解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
∵等差数列{an}的各项均为正数,a1=1,b1=2,
∴an=1+(n﹣1)d,bn=2qn﹣1,d>0,
∵b2S2=16,b3S3=72,
∴,
解得d=q=2,
∴an=2n﹣1,bn=2n.
(2)∵a1=1,d=2,
∴Sn=n+n(n﹣1) 2=n2,
可得=,
前n项和Tn=+++…+,
Tn=+++…+,
相减可得Tn=++++…+﹣,
设An=++++…+,
An=++++…+,
两式相减可得,
An=+2(++++…+)﹣
=+2 ﹣,
化简可得An=3﹣.
即有Tn=3﹣﹣,
可得Tn=6﹣.
21.已知函数f(x)=alnx+bx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为x﹣2y﹣2=0.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x>1时,f(x)+<0恒成立,求实数k的取值范围.
【考点】利用导数研究曲线上某点切线方程;导数在最大值、最小值问题中的应用.
【分析】(Ⅰ)求导数得f′(x)=+b,由导数几何意义得曲线y=f(x)在点(1,f(1))处的切线斜率为k=f′(1)=,且f(1)=,联立求得a=1,b=﹣,从而确定f(x)的解析式;
(Ⅱ)由(Ⅰ)知,不等式等价于lnx﹣+<0,参变分离为k<﹣xlnx,利用导数求右侧函数的最小值即可.
【解答】解:(Ⅰ)∵f(x)=alnx+bx,∴f′(x)=+b.
∵直线x﹣2y﹣2=0的斜率为,且曲线y=f(x)过点(1,﹣),
∴即解得a=1,b=﹣.
所以f(x)=lnx﹣x;
(Ⅱ)由(Ⅰ)得当x>1时,f(x)+<0恒成立即lnx﹣+<0,等价于k<﹣xlnx.
令g(x)=﹣xlnx,则g′(x)=x﹣1﹣lnx.
令h(x)=x﹣1﹣lnx,则h′(x)=1﹣.
当x>1时,h′(x)>0,函数h(x)在(1,+∞)上单调递增,故h(x)>h(1)=0.
从而,当x>1时,g′(x)>0,即函数g(x)在(1,+∞)上单调递增,
故g(x)>g(1)=.
因此,当x>1时,k<﹣xlnx恒成立,则k≤.
∴k的取值范围是(﹣∞,].
22.设椭圆C:
=1的左右焦点分别为F1,F2,直线y=x﹣1过椭圆的焦点F2且与椭圆交于P,Q两点,若△F1PQ周长为4.
(1)求椭圆的方程;
(2)圆C′:x2+y2=1,直线y=kx+m与圆C′相切且与椭圆C交于不同的两点A,B,O为坐标原点.若 =λ,且≤λ≤,求△OAB的取值范围.
【考点】椭圆的简单性质.
【分析】(1)由已知F2(1,0),即c=1,△F1PQ周长为4,可得a,即可求椭圆的方程;
(2)设A(x1,y1),B(x2,y2),则由y=kx+m(b>0)与圆x2+y2=1相切,由y=kx+m代入椭圆方程,利用 =λ,求出≤k2≤1,再由弦长公式,求出|AB|的长,用点到直线的距离公式求出点O到直线AB的距离,由此可以导出△OAB面积S的取值范围.
【解答】解:(1)由已知F2(1,0),即c=1,
△F1PQ周长为4,可得4a=4,即a=,
∴b=1,
∴椭圆的方程为;
(2)y=kx+m(b>0)与圆x2+y2=1相切,则,
即m2=k2+1,k≠0,
设A(x1,y1),B(x2,y2),
则由y=kx+m代入椭圆方程,消去y得(2k2+1)x2+4kmx+2m2﹣2=0
又△=8k2>0
x1+x2=﹣,x1x2=,
=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2==λ,
∵≤λ≤,
∴≤≤,
∴≤k2≤1,
由弦长公式,得|AB|=
又点O到直线AB的距离d=1
∴S△OAB===,
∵≤k2≤1,
∴4≤(1+2k2)2≤9,
∴S△OAB∈[,].
2016年9月16日
一、选择题(每小题5分,共60分)
1.已知复数z=﹣i+2,则z的虚部为( )
A.i
B.﹣1
C.1
D.﹣i
2.已知a,b,c,d为实数,且c>d,则“a>b”是“a+c>b+d”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
3.下列函数求导运算正确的个数为( )
①(3x)′=3xlog3e;
②(log2x)′=
③(ex)′=ex;
④()′=x;
⑤(x ex)′=ex+1.
A.1
B.2
C.3
D.4
4.已知A、B、C三点不共线,O是平面ABC外的任一点,下列条件中能确定点M与点A、B、C一定共面的是( )
A.
B.
C.
D.
5.(1)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.
(2)“x=1”是“x2﹣4x+3=0”的充要条件;
(3)若p∧q为假命题,则p、q均为假命题.
(4)对于命题p: x0∈R,x+2x0+2≤0,则¬p: x∈R,x2+2x+2>0.
上面四个命题中正确的个数是( )
A.1
B.2
C.3
D.4
6.在△ABC中,角A、B、C所对的边长分别为a,b,c,若A=60°,B=45°,,则b=( )
A.
B.2
C.
D.
7.抛物线y2+4x=0上的点P到直线x=2的距离等于4,则P到焦点F的距离|PF|=( )
A.1
B.2
C.3
D.4
8.在正三棱柱ABC﹣A1B1C1中,已知AB=2,CC1=,则异面直线AB1和BC1所成角的余弦值为( )
A.0
B.
C.
D.
9.等比数列{an}中,a4=2,a5=5,则数列{lgan}的前8项和等于( )
A.6
B.5
C.4
D.3
10.双曲线C:﹣=1(a>0,b>0)的右焦点为F,若以点F为圆心,半径为a的圆与双曲线C的渐近线相切,则双曲线C的离心率等于( )
A.
B.
C.2
D.2
11.如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为(n≥2),并且相邻两行数之间有一定的关系,则第7行第4个数(从左往右数)为( )
A.
B.
C.
D.
12.若函数f(x)=+2x(a>0,b≥0)在区间[1,2]上单调递减,则a(b﹣1)的最大值为( )
A.4
B.
C.
D.
二、填空题(每小题5分,共20分)
13.(理)______.
14.函数f(x)=x3﹣3x2+1在x=______处取得极小值.
15.若实x,y满足不等式组目标函t=x﹣2y的最大值为2,则实a的值是______.
16.已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=2且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为______.
三、解答题(共70分)
17.已知m∈R,设命题p:方程+=1表示焦点在y轴上的椭圆;命题q:函数f(x)=3x2+2mx+m+有零点.
(1)若¬p为真命题,求m的取值范围;
(2)若“p∨q”为真,求m的取值范围.
18.如图所示,△ABC中,AC=1,AB=2,∠ACB=,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
(1)求证:AD∥平面PCE;
(2)求二面角P﹣CE﹣B的余弦值.
19.如图,在△ABC中,∠ABC=90°,,BC=1,P为△ABC内一点,∠BPC=90°
(Ⅰ)若,求PA;
(Ⅱ)若∠APB=150°,求tan∠PBA.
20.已知数列{an}是各项均为正数的等差数列,首项a1=1,其前n项和为Sn;数列{bn}是等比数列,首项b1=2,且b2S2=16,b3S3=72.
(1)求数列{an},{bn}的通项公式;
(2)若,求数列{cn}的前n项和Tn.
21.已知函数f(x)=alnx+bx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为x﹣2y﹣2=0.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x>1时,f(x)+<0恒成立,求实数k的取值范围.
22.设椭圆C:
=1的左右焦点分别为F1,F2,直线y=x﹣1过椭圆的焦点F2且与椭圆交于P,Q两点,若△F1PQ周长为4.
(1)求椭圆的方程;
(2)圆C′:x2+y2=1,直线y=kx+m与圆C′相切且与椭圆C交于不同的两点A,B,O为坐标原点.若 =λ,且≤λ≤,求△OAB的取值范围.
2015-2016学年湖南省株洲五中高二(下)入学数学试卷(理科)
参考答案与试题解析
一、选择题(每小题5分,共60分)
1.已知复数z=﹣i+2,则z的虚部为( )
A.i
B.﹣1
C.1
D.﹣i
【考点】复数的基本概念.
【分析】直接利用复数的概念写出结果即可.
【解答】解:复数z=﹣i+2,则z的虚部为:﹣1.
故选:B.
2.已知a,b,c,d为实数,且c>d,则“a>b”是“a+c>b+d”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】根据不等式的性质,结合充分条件和必要条件的定义进行判断即可.
【解答】解:若a>b,∵c>d,∴a+c>b+d成立.
当c=3,d=2,a=b=0时,满足a+c>b+d,但a>b不成立.
故“a>b”是“a+c>b+d”的充分不必要条件.
故选:A.
3.下列函数求导运算正确的个数为( )
①(3x)′=3xlog3e;
②(log2x)′=
③(ex)′=ex;
④()′=x;
⑤(x ex)′=ex+1.
A.1
B.2
C.3
D.4
【考点】导数的运算.
【分析】根据(ax)′=axlna,(logax)′=,(lnx)'=即可作出判断.
【解答】解:①(3x)′=3xln3,故错误;
②(log2x)′=,故正确;
③(ex)'=ex,故正确;
④()′=﹣,故错误;
⑤(x ex)′=ex+x ex,故错误.
故选:B.
4.已知A、B、C三点不共线,O是平面ABC外的任一点,下列条件中能确定点M与点A、B、C一定共面的是( )
A.
B.
C.
D.
【考点】共线向量与共面向量.
【分析】根据共面向量定理,说明M、A、B、C共面,判断选项的正误.
【解答】解:由共面向量定理,
说明M、A、B、C共面,
可以判断A、B、C都是错误的,
则D正确.
故选D.
5.(1)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.
(2)“x=1”是“x2﹣4x+3=0”的充要条件;
(3)若p∧q为假命题,则p、q均为假命题.
(4)对于命题p: x0∈R,x+2x0+2≤0,则¬p: x∈R,x2+2x+2>0.
上面四个命题中正确的个数是( )
A.1
B.2
C.3
D.4
【考点】命题的真假判断与应用.
【分析】(1)根据逆否命题的定义进行判断,
(2)根据充分条件和必要条件的定义进行判断即可
(3)根据复合命题真假之间的关系进行判断
(4)根据特称命题的否定是全称命题进行判断即可.
【解答】解:(1)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”.正确,
(2)由x2﹣4x+3=0得x=1或x=3,则“x=1”是“x2﹣4x+3=0”的充分不必要条件;故(2)错误,
(3)若p∧q为假命题,则p、q至少有一个为假命题.故(3)错误,
(4)对于命题p: x0∈R,x+2x0+2≤0,则¬p: x∈R,x2+2x+2>0.正确,
故正确的是(1)(4),
故选:B.
6.在△ABC中,角A、B、C所对的边长分别为a,b,c,若A=60°,B=45°,,则b=( )
A.
B.2
C.
D.
【考点】正弦定理.
【分析】由正弦定理的式子,结合题中数据加以计算,可得b==2.
【解答】解:∵△ABC中,A=60°,B=45°,,
∴由正弦定理,得b===2.
故选:B
7.抛物线y2+4x=0上的点P到直线x=2的距离等于4,则P到焦点F的距离|PF|=( )
A.1
B.2
C.3
D.4
【考点】抛物线的简单性质.
【分析】由抛物线的方程求出其焦点坐标和准线方程,利用已知求得P到准线的距离,则答案可求.
【解答】解:由y2+4x=0,得y2=﹣4x,
∴抛物线的焦点F(﹣1,0),准线方程为x=1.
如图:
∵P到直线x=2的距离为4,∴P到准线x=1的距离为3,
则P到焦点F的距离|PF|=3.
故选:C.
8.在正三棱柱ABC﹣A1B1C1中,已知AB=2,CC1=,则异面直线AB1和BC1所成角的余弦值为( )
A.0
B.
C.
D.
【考点】异面直线及其所成的角.
【分析】连接B1C交BC1于E,连接DE,利用四边形BCC1B1是平行四边形及其三角形的中位线定理证明DE∥AB1,可得∠DEB或其补角为异面直线AB1与BC1所成的角,再利用余弦定理即可得出.
【解答】解:如图所示
连接B1C交BC1于E,连接DE,
∵四边形BCC1B1是平行四边形,∴B1E=EC.
又AD=DC.
∴DE∥AB1,
∴∠DEB或其补角为异面直线AB1与BC1所成的角,
在△DEB中,DE=,BD=,BE=.
∴cos∠DEB==0,
∴异面直线AB1和BC1所成角的余弦值为0.
故选:A.
9.等比数列{an}中,a4=2,a5=5,则数列{lgan}的前8项和等于( )
A.6
B.5
C.4
D.3
【考点】等比数列的前n项和.
【分析】利用等比数列的性质可得a1a8=a2a7=a3a6=a4a5=10.再利用对数的运算性质即可得出.
【解答】解:∵数列{an}是等比数列,a4=2,a5=5,
∴a1a8=a2a7=a3a6=a4a5=10.
∴lga1+lga2+…+lga8
=lg(a1a2 … a8)
=
4lg10
=4.
故选:C.
10.双曲线C:﹣=1(a>0,b>0)的右焦点为F,若以点F为圆心,半径为a的圆与双曲线C的渐近线相切,则双曲线C的离心率等于( )
A.
B.
C.2
D.2
【考点】双曲线的简单性质.
【分析】根据双曲线方程表示出F坐标,以及渐近线方程,由以点F为圆心,半径为a的圆与双曲线C的渐近线相切,得到圆心F到渐近线距离d=r,整理得到a=b,再利用双曲线的简单性质及离心率公式计算即可.
【解答】解:根据题意得:圆心F(c,0),半径为a,双曲线渐近线方程为y=±x,即±bx﹣ay=0,
∵以点F为圆心,半径为a的圆与双曲线C的渐近线相切,且c2=a2+b2,
∴圆心F到渐近线的距离d==a,即a=b,
∴c====a,
则双曲线C的离心率e==,
故选:B.
11.如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为(n≥2),并且相邻两行数之间有一定的关系,则第7行第4个数(从左往右数)为( )
A.
B.
C.
D.
【考点】归纳推理.
【分析】根据每个数是它下一行左右相邻两数的和,先求出第5,6,7三行的第2个数,再求出6,7两行的第3个数,求出第7行的第4个数.
【解答】解:设第n行第m个数为a(n,m),
由题意知a(6,1)=,a(7,1)=,
∴a(7,2)=a(6,1)﹣a(7,1)=﹣=,
a(6,2)=a(5,1)﹣a(6,1)=﹣=,
a(7,3)=a(6,2)﹣a(7,2)=﹣=,
a(6,3)=a(5,2)﹣a(6,2)=﹣=,
∴a(7,4)=a(6,3)﹣a(7,3)=﹣=.
故选A.
12.若函数f(x)=+2x(a>0,b≥0)在区间[1,2]上单调递减,则a(b﹣1)的最大值为( )
A.4
B.
C.
D.
【考点】利用导数研究函数的单调性;基本不等式.
【分析】求得f(x)的导数,由题意可得f′(x)≤0在区间[1,2]上恒成立,可得,作出不等式组在第四象限的可行域,再由目标函数表示的双曲线,结合直线与双曲线相切,求得导数,设出切点,解方程可得切点,进而得到所求最大值.
【解答】解:函数f(x)=ax3+(b﹣8)x2+2x(a>0,b≥0),
f′(x)=ax2+(b﹣8)x+2,
由题意可得f′(x)≤0在区间[1,2]上恒成立,
即有,即为,(
)
以(a,b)为坐标,作出不等式组(
)在第一象限的可行域,如图:
,
令t=a(b﹣1),可得b=+1,此函数的图象为双曲线,
当直线b=7﹣2a与双曲线b=+1相切时,t取得最大值,
由得:2a2﹣6a+t=0,
△=36﹣8t=0,
解得t=,
故选:C.
二、填空题(每小题5分,共20分)
13.(理) π+2 .
【考点】定积分.
【分析】根据定积分的定义,找出三角函数的原函数然后代入计算即可.
【解答】解:(x+sinx)=+1﹣(﹣1)=π+2,
故答案为π+2.
14.函数f(x)=x3﹣3x2+1在x= 2 处取得极小值.
【考点】利用导数研究函数的极值.
【分析】首先求导可得f′(x)=3x2﹣6x,解3x2﹣6x=0可得其根,再判断导函数的符号即可.
【解答】解:f′(x)=3x2﹣6x,
令f′(x)=3x2﹣6x=0得x1=0,x2=2,
且x∈(﹣∞,0)时,f′(x)>0;x∈(0,2)时,f′(x)<0;x∈(2,+∞)时,f′(x)>0,
故f(x)在x=2出取得极小值.
故答案为:2.
15.若实x,y满足不等式组目标函t=x﹣2y的最大值为2,则实a的值是 2 .
【考点】简单线性规划.
【分析】画出约束条件表示的可行域,然后根据目标函数t=x﹣2y的最大值为2,确定约束条件中a值.
【解答】解:由题意约束条件的可行域是图中的阴影部分,
目标函数t=x﹣2y的最大值为2,
就是直线t=x﹣2y,经过直线x=2与直线x+2y﹣a=0的交点,
也就是x=2与x﹣2y=2的交点A(2,0),
所以a=x+2y=2+2×0=2,
则实a的值是2,
故答案为:2.
16.已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=2且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为 .
【考点】余弦定理;正弦定理.
【分析】由正弦定理化简已知可得2a﹣b2=c2﹣bc,结合余弦定理可求A的值,由基本不等式可求bc≤4,再利用三角形面积公式即可计算得解.
【解答】解:因为:(2+b)(sinA﹣sinB)=(c﹣b)sinC
(2+b)(a﹣b)=(c﹣b)c
2a﹣b2=c2﹣bc,
又因为:a=2,
所以:,
△ABC面积,
而b2+c2﹣a2=bc
b2+c2﹣bc=a2
b2+c2﹣bc=4
bc≤4
所以:,即△ABC面积的最大值为.
故答案为:.
三、解答题(共70分)
17.已知m∈R,设命题p:方程+=1表示焦点在y轴上的椭圆;命题q:函数f(x)=3x2+2mx+m+有零点.
(1)若¬p为真命题,求m的取值范围;
(2)若“p∨q”为真,求m的取值范围.
【考点】复合命题的真假.
【分析】(1)p:m﹣1>5﹣m>0,解出m范围,由于 p为真命题,可得p为假命题,即可得出.
(2)函数有零点,可得△≥0,由于“p∨q”为真,可得m∈P∪Q.
【解答】解:(1)p:m﹣1>5﹣m>0,∴3<m<5,…
∵ p为真命题,∴p为假命题…
∴m≤3或m≥5.…
(2)函数有零点,∴△≥0,≥0,…
∴m≥4或m≤﹣1.…
设Q={m|m≥4或m≤﹣1},P={m|3<m<5}.
∵“p∨q”为真,∴m∈P∪Q,即m>3或m≤﹣1.…
18.如图所示,△ABC中,AC=1,AB=2,∠ACB=,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
(1)求证:AD∥平面PCE;
(2)求二面角P﹣CE﹣B的余弦值.
【考点】二面角的平面角及求法;直线与平面平行的判定.
【分析】(Ⅰ)设BD∩CE=0,连结OP,则OP∥AD,由此能证明AD∥平面PCE;
(2)以C为原点,CA为x轴,CB为y轴,CD为z轴,建立空间直角坐标系,利用向量法能求出二面角P﹣CE﹣B的余弦值.
【解答】解:(1)证明:设BD∩CE=0,连结OP,
∵正方形BCDE对角线互相平分,∴O是BD中点,
∵P为AB的中点,∴OP∥AD,
∵AD 平面PCE,OP 平面PCE,
∴AD∥平面PCE;
(2)∵△ABC中,AC=1,AB=2,∠ACB=,
P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直,
∴CD⊥平面ABC,
以C为原点,CA为x轴,CB为y轴,CD为z轴,
建立空间直角坐标系,
C(0,0,0),A(1,0,0),B(0,2,0),
P(),E(0,2,2),
=(),=(0,2,2),
设平面PCE的法向量=(x,y,z),
则,取x=2,得=(2,﹣2,2),
平面BCE的法向量=(1,0,0),
设二面角P﹣CE﹣B的平面角为θ,
则cosθ===.
∴二面角P﹣CE﹣B的余弦值为.
19.如图,在△ABC中,∠ABC=90°,,BC=1,P为△ABC内一点,∠BPC=90°
(Ⅰ)若,求PA;
(Ⅱ)若∠APB=150°,求tan∠PBA.
【考点】余弦定理;正弦定理.
【分析】(I)在Rt△PBC,利用边角关系即可得到∠PBC=60°,得到∠PBA=30°.在△PBA中,利用余弦定理即可求得PA.
(II)设∠PBA=α,在Rt△PBC中,可得PB=sinα.在△PBA中,由正弦定理得,即,化简即可求出.
【解答】解:(I)在Rt△PBC中,
=,∴∠PBC=60°,∴∠PBA=30°.
在△PBA中,由余弦定理得PA2=PB2+AB2﹣2PB ABcos30°==.
∴PA=.
(II)设∠PBA=α,在Rt△PBC中,PB=BCcos(90°﹣α)=sinα.
在△PBA中,由正弦定理得,即,
化为.∴.
20.已知数列{an}是各项均为正数的等差数列,首项a1=1,其前n项和为Sn;数列{bn}是等比数列,首项b1=2,且b2S2=16,b3S3=72.
(1)求数列{an},{bn}的通项公式;
(2)若,求数列{cn}的前n项和Tn.
【考点】数列的求和.
【分析】(1)由已知条件,利用等差数列、等比数列的通项公式、前n项和列出方程组,求出等差数列的公差和等比数列的公比,由此能求出an与bn;
(2)由(1)能推导出Sn=n2,两次运用数列的求和方法:错位相减法,结合等比数列的求和公式.
【解答】解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
∵等差数列{an}的各项均为正数,a1=1,b1=2,
∴an=1+(n﹣1)d,bn=2qn﹣1,d>0,
∵b2S2=16,b3S3=72,
∴,
解得d=q=2,
∴an=2n﹣1,bn=2n.
(2)∵a1=1,d=2,
∴Sn=n+n(n﹣1) 2=n2,
可得=,
前n项和Tn=+++…+,
Tn=+++…+,
相减可得Tn=++++…+﹣,
设An=++++…+,
An=++++…+,
两式相减可得,
An=+2(++++…+)﹣
=+2 ﹣,
化简可得An=3﹣.
即有Tn=3﹣﹣,
可得Tn=6﹣.
21.已知函数f(x)=alnx+bx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为x﹣2y﹣2=0.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x>1时,f(x)+<0恒成立,求实数k的取值范围.
【考点】利用导数研究曲线上某点切线方程;导数在最大值、最小值问题中的应用.
【分析】(Ⅰ)求导数得f′(x)=+b,由导数几何意义得曲线y=f(x)在点(1,f(1))处的切线斜率为k=f′(1)=,且f(1)=,联立求得a=1,b=﹣,从而确定f(x)的解析式;
(Ⅱ)由(Ⅰ)知,不等式等价于lnx﹣+<0,参变分离为k<﹣xlnx,利用导数求右侧函数的最小值即可.
【解答】解:(Ⅰ)∵f(x)=alnx+bx,∴f′(x)=+b.
∵直线x﹣2y﹣2=0的斜率为,且曲线y=f(x)过点(1,﹣),
∴即解得a=1,b=﹣.
所以f(x)=lnx﹣x;
(Ⅱ)由(Ⅰ)得当x>1时,f(x)+<0恒成立即lnx﹣+<0,等价于k<﹣xlnx.
令g(x)=﹣xlnx,则g′(x)=x﹣1﹣lnx.
令h(x)=x﹣1﹣lnx,则h′(x)=1﹣.
当x>1时,h′(x)>0,函数h(x)在(1,+∞)上单调递增,故h(x)>h(1)=0.
从而,当x>1时,g′(x)>0,即函数g(x)在(1,+∞)上单调递增,
故g(x)>g(1)=.
因此,当x>1时,k<﹣xlnx恒成立,则k≤.
∴k的取值范围是(﹣∞,].
22.设椭圆C:
=1的左右焦点分别为F1,F2,直线y=x﹣1过椭圆的焦点F2且与椭圆交于P,Q两点,若△F1PQ周长为4.
(1)求椭圆的方程;
(2)圆C′:x2+y2=1,直线y=kx+m与圆C′相切且与椭圆C交于不同的两点A,B,O为坐标原点.若 =λ,且≤λ≤,求△OAB的取值范围.
【考点】椭圆的简单性质.
【分析】(1)由已知F2(1,0),即c=1,△F1PQ周长为4,可得a,即可求椭圆的方程;
(2)设A(x1,y1),B(x2,y2),则由y=kx+m(b>0)与圆x2+y2=1相切,由y=kx+m代入椭圆方程,利用 =λ,求出≤k2≤1,再由弦长公式,求出|AB|的长,用点到直线的距离公式求出点O到直线AB的距离,由此可以导出△OAB面积S的取值范围.
【解答】解:(1)由已知F2(1,0),即c=1,
△F1PQ周长为4,可得4a=4,即a=,
∴b=1,
∴椭圆的方程为;
(2)y=kx+m(b>0)与圆x2+y2=1相切,则,
即m2=k2+1,k≠0,
设A(x1,y1),B(x2,y2),
则由y=kx+m代入椭圆方程,消去y得(2k2+1)x2+4kmx+2m2﹣2=0
又△=8k2>0
x1+x2=﹣,x1x2=,
=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2==λ,
∵≤λ≤,
∴≤≤,
∴≤k2≤1,
由弦长公式,得|AB|=
又点O到直线AB的距离d=1
∴S△OAB===,
∵≤k2≤1,
∴4≤(1+2k2)2≤9,
∴S△OAB∈[,].
2016年9月16日
同课章节目录
