北师大版数学七年级上册第二章有理数及其运算2.1有理数课件
文档属性
| 名称 | 北师大版数学七年级上册第二章有理数及其运算2.1有理数课件 |  | |
| 格式 | zip | ||
| 文件大小 | 880.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-16 13:46:25 | ||
图片预览






文档简介
课件29张PPT。2.1 有理数第二章 有理数及其运算
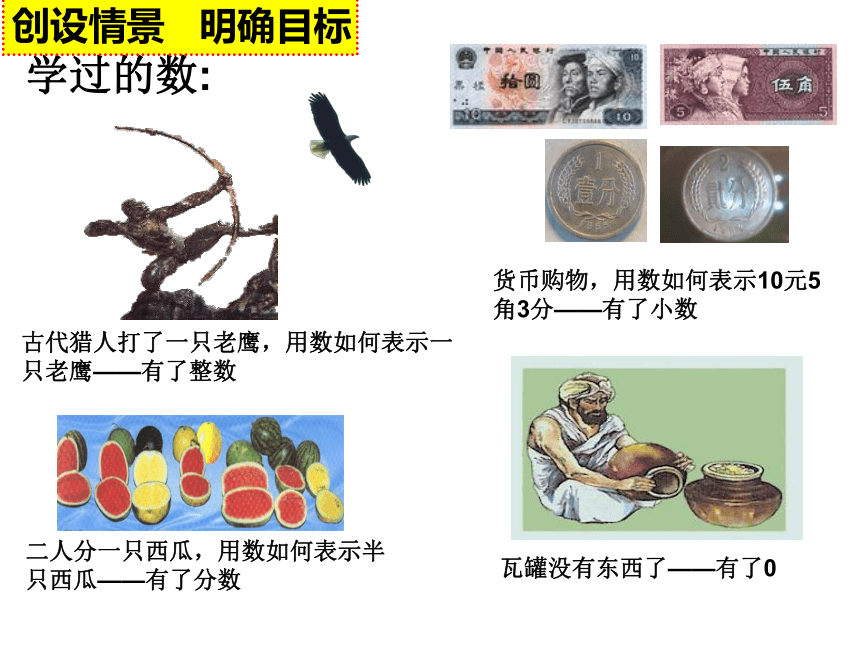
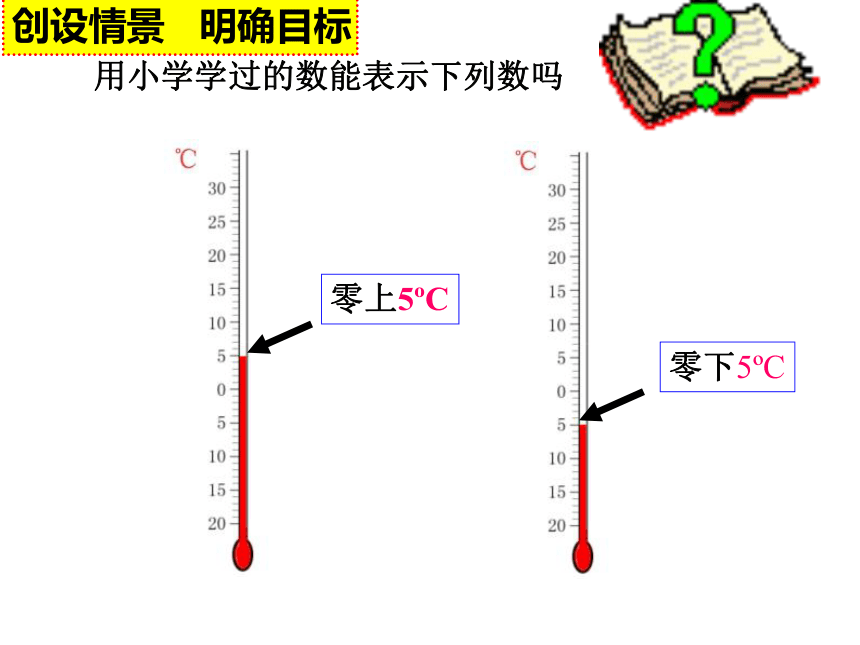
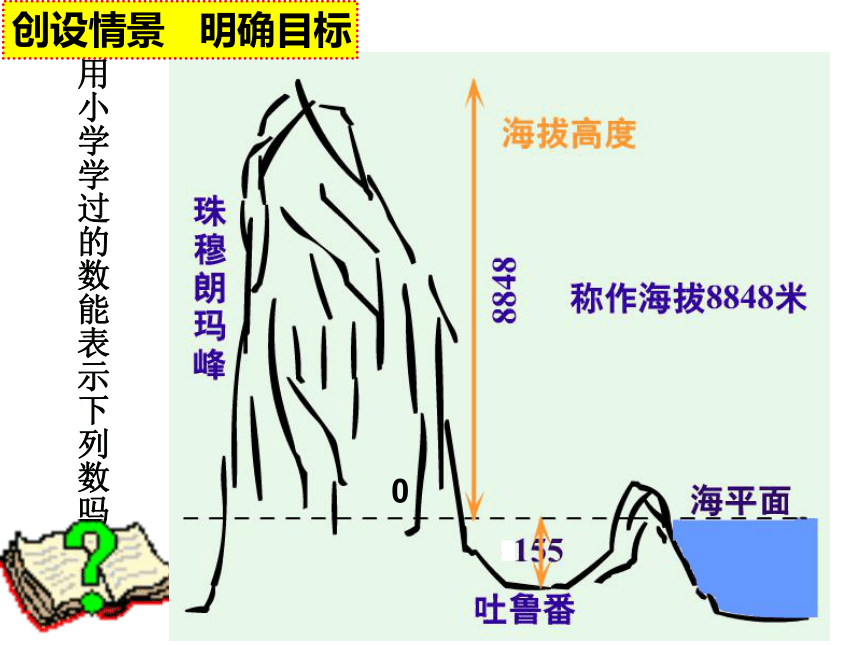
学过的数:古代猎人打了一只老鹰,用数如何表示一只老鹰——有了整数 二人分一只西瓜,用数如何表示半只西瓜——有了分数货币购物,用数如何表示10元5角3分——有了小数创设情景 明确目标零上5oC零下5oC用小学学过的数能表示下列数吗创设情景 明确目标用小学学过的数能表示下列数吗0创设情景 明确目标1.会判断一个数是正数还是负数,能用正、负数表示具有相反意义的量.
2.理解有理数的意义,会将有理数正确分类.学习目标活动一:阅读教材内容,思考:正数与负数是怎样产生的?它们在生活中有何作用?你能举例说一说吗?
(1)生活中具有相反意义的量
如:运进5吨与运出3吨;上升7米与下降8米;向东50米与向西47米等都是生活中遇到的具有相反意义的量.
请你也举一个具有相反意义量的例子:
_______________________________.
(2)负数的产生同样是生活和生产的需要.探究点一:正数与负数的意义合作探究 达成目标【展示点评】用正数和负数如何表示具有相反意义的量,关键是看规定哪种意义的量为正,则与之相反意义的量为负.【小组讨论1】用正数和负数表示具有相反意义的量
观察下面给出的每一对数量,指出各对数量有什么共同特点.
⑴零上3℃和零下12℃; ⑵收入800元和支出500元;
⑶增加5kg和减少2kg; ⑷水位升高0.5m和降低1.3m
通过观察,发现这里给出的每一对数量,都有一个共同的特点:
每个语句中都含有一对具有相反意义的量:如“零上”和“ ”、“收入”和“ ”、“增加”和“ ”、“升高”和“ ”.探究点一:正数与负数的意义合作探究 达成目标【反思小结】一般地,我们把上升、运进、零上、收入、前进、高出等规定为正的,而与它相反的量,如:下降、运出、零下、支出、后退、低于等规定为负的.正的量就用小学里学过的数表示,有时也在它前面放上一个“+”(读作正)号,如前面的5、7、50;负的量用小学学过的数前面放上“—”(读作负)号来表示,如上面的-3、-8、-47. 1.(2012·乐山中考)如果规定收入为正,支出为负.收入500元
记作500元,那么支出237元应记作( )
A.-500元 B.-237元
C.237元 D.500元
【解析】选B.因支出为负,故支出237元应记作-237元.试一试2.如果用+0.02克表示一只乒乓球质量超出标准质量0.02克,
那么一只乒乓球质量低于标准质量0.02克记为( )
A.+0.02克 B.-0.02克
C.0克 D.+0.04克
【解析】选B.根据题意可得:超出标准质量记为“+”,所以
低于标准质量记为“-”,因此,低于标准质量0.02克记为
-0.02克.3.有四包真空小包装火腿,每包以标准克数(450克)为基准,
超过的克数记作正数,不足的克数记作负数,以下数据是记录
结果,其中表示实际克数最接近标准克数的是( )
A.+2 B.-3
C.+3 D.+4
【解析】选A.通过计算得A为452,B为447,C为453,D为454,
故A最接近标准克数.4.如果盈利10%记为“+10%”,那么亏损6%记为( )
A.-16% B.-6%
C.+6% D.+4%
【解析】选B.根据题意可得:盈利为“+”,则亏损为“-”,
所以亏损6%记为:-6%.5.(2012·连云港中考)某药品说明书上标明药品保存的温度是
(20±2)℃,该药品在_______℃范围内保存才合适.
【解析】温度是20 ℃±2 ℃,表示最低温度是20-2=18(℃),
最高温度是20+2=22(℃),即18~22 ℃之间是合适温度.
答案:18~226.某公交车原有22人,经过3个站点时上下车情况如下(上车为
正,下车为负):(4,-8),(-5,6),(-3,2),求经过3个站
点后车上剩余的人数.
【解析】第一站剩余人数为:22+4-8=18(人);
第二站剩余人数为:18-5+6=19(人);
第三站剩余人数为:19-3+2=18(人).
故最后车上剩余18人.活动二:阅读教材,思考:什么样的数是正数?负数呢?0是正数吗?0是负数吗?什么样的数是有理数?如何对有理数进行分类?探究点二:有理数的概念及其分类合作探究 达成目标【展示点评】正数和负数的概念:
⑴像5,1.2, ,……这样的数叫做 ,它们都比____大;
⑵在正数前面加上“-”号的数叫做 ,如-10,-3等,它们都比____小;
⑶0 既不是 ,也不是 .0是_______和________的分界点,0是____数,也是____数,也是____数.
有理数的概念:整数与分数统称为有理数.有理数的判断方法:①正整数、0、负整数都是有理数.②正分数和负分数都是有理数.【小组讨论2】理解正数和负数时,有什么要注意的问题?对有理数进行分类有哪些标准?如何分?探究点二:有理数的概念及其分类合作探究 达成目标【反思小结】理解正数和负数时,①对于正数和负数的意义,不能简单地理解为带“+”号的数是正数,带“-”号的数是负数.②负数是在正数前面加上一个“-”号,如-5,- (+7)等都是负数,负数中的“-”号不能省略,如-5省略“-”号就是5,变成 正数 了.③0:0既不是正数也不是负数.探究点二:有理数的概念及其分类合作探究 达成目标有理数的分类:正分数负有理数负分数
观察下列各数的特点并分类,填到相应的位置中.
1,2,3,0,-1,-2,-3, , ,5.2, , , -3.5
正整数:______
零:__
负整数:_________
正分数:_________
负分数:___________1,2,30-1,-2,-3例1例2 将下列各数填在相应的大括号内:
5,-2,-0.3, , 0, 5.7, 102, -17
正数:{_________……};
负数:{_________……};
整数:{_________……};
分数:{_________……}.
【总结提升】有理数的分类中的四点注意
1.相对性:正数是相对负数而言的,整数是相对分数而言的.
2.特殊0:0既不是正数,也不是负数,但0是整数.
3.多属性:同一个数,可能属于多个不同的集合.如5既是正数
又是整数.
4.提醒:分数包括有限小数和无限循环小数.练一练:
1.-3.782( )
A.是负数,不是分数
B.不是分数,是有理数
C.是负数,也是分数
D.是分数,不是有理数
【解析】选C.-3.782是负数,也属于分数,还是有理数.2.下列各数:-6,-3.14, ,0,4,-0.2中,整数的个数
为( )
A.2个 B.3个 C.4个 D.5个
【解析】选B.-6是负整数,-3.14是负小数, 是分数,0是
整数,4是整数,-0.2是负小数,所以只有-6,0,4是整数,
所以整数共有3个.3.下列说法正确的个数是( )
① 是负分数;
②1.3不是整数;
③非负有理数不包括0;
④正整数、负整数统称整数;
⑤0是最小的有理数.
A.1个 B.2个 C.3个 D.4个【解析】选B.因为 是负分数,所以①正确;因为1.3是小
数不是整数,所以②正确;因为非负有理数包括0和正有理
数,所以③错误;因为正整数、0、负整数统称为整数,所以
④错误;因为没有最小的有理数,所以0是最小的有理数错
误,即⑤错误.故正确的共有2个.【高手支招】分数和有理数的关系
1.凡是分数都是有理数.
2.有限小数和无限循环小数都可以化为分数,所以是有理数,
不是所有的小数都能表示成分数,如“π”就不能表示成分数.【想一想错在哪?】下面关于“0”的一些说法中正确的是
____________.
①0既不是正数也不是负数;
②0是最小的自然数;
③0是最小的正数;
④0是最小的非负数;
⑤0既不是奇数也不是偶数;
⑥亏损200元,记为-200元,则盈利200元,记为:0元.达标检测 反思目标1. 下列各数中,为负数的是( )
A.0 B.-2 C.1 D.B2. 如果+3吨表示运入仓库的大樱桃吨数,那么运出5吨
大樱桃表示为( )
A.-5吨 B.+5吨 C.-3吨 D.+3吨3. 某项科学研究,以45分钟为1个时间单位,并记每天
上午10时为0,10时以前记为负,10时以后记为正.
例如,9:15记为-1,10:45记为1等等.依此类推
,上午7:45应记为( )
A.-2 B.-2.5 C.-3 D.-7.45AC达标检测 反思目标4. 如果海平面的高度为0米,用负数表示低于海平面的某地的高度,一潜水艇在海平 面 下40米处航行,一条鲨鱼在潜水艇上方10米处游动,那么鲨鱼的高度是________米.5. 把下列各数填入相应的括号内.
1, ,8.9,-2.8,+100, ,-0.03,0,-7
正整数:{ …}
负整数:{ …}
正分数:{ …}
分数:{ …}
自然数:{ …} -30 (打“√”或“×”)
(1)上升5米,记作+5米,则下降5米记作-5米.( )
(2)一个有理数不是正数就是负数.( )
(3)一个有理数不是整数就是分数.( )
(4)负分数一定是负有理数.( )
(5)整数都是正数.( )√×√√×1.用正数和负数表示具有相反意义的量,如气温零上20℃记作:________,盈利3万元记作:________,注意表示时需要带上______.
2.有理数的分类:⑴按符号分类:
⑵按定义分类:
总结梳理 内化目标 +20 ℃ +3万元 单位
2.理解有理数的意义,会将有理数正确分类.学习目标活动一:阅读教材内容,思考:正数与负数是怎样产生的?它们在生活中有何作用?你能举例说一说吗?
(1)生活中具有相反意义的量
如:运进5吨与运出3吨;上升7米与下降8米;向东50米与向西47米等都是生活中遇到的具有相反意义的量.
请你也举一个具有相反意义量的例子:
_______________________________.
(2)负数的产生同样是生活和生产的需要.探究点一:正数与负数的意义合作探究 达成目标【展示点评】用正数和负数如何表示具有相反意义的量,关键是看规定哪种意义的量为正,则与之相反意义的量为负.【小组讨论1】用正数和负数表示具有相反意义的量
观察下面给出的每一对数量,指出各对数量有什么共同特点.
⑴零上3℃和零下12℃; ⑵收入800元和支出500元;
⑶增加5kg和减少2kg; ⑷水位升高0.5m和降低1.3m
通过观察,发现这里给出的每一对数量,都有一个共同的特点:
每个语句中都含有一对具有相反意义的量:如“零上”和“ ”、“收入”和“ ”、“增加”和“ ”、“升高”和“ ”.探究点一:正数与负数的意义合作探究 达成目标【反思小结】一般地,我们把上升、运进、零上、收入、前进、高出等规定为正的,而与它相反的量,如:下降、运出、零下、支出、后退、低于等规定为负的.正的量就用小学里学过的数表示,有时也在它前面放上一个“+”(读作正)号,如前面的5、7、50;负的量用小学学过的数前面放上“—”(读作负)号来表示,如上面的-3、-8、-47. 1.(2012·乐山中考)如果规定收入为正,支出为负.收入500元
记作500元,那么支出237元应记作( )
A.-500元 B.-237元
C.237元 D.500元
【解析】选B.因支出为负,故支出237元应记作-237元.试一试2.如果用+0.02克表示一只乒乓球质量超出标准质量0.02克,
那么一只乒乓球质量低于标准质量0.02克记为( )
A.+0.02克 B.-0.02克
C.0克 D.+0.04克
【解析】选B.根据题意可得:超出标准质量记为“+”,所以
低于标准质量记为“-”,因此,低于标准质量0.02克记为
-0.02克.3.有四包真空小包装火腿,每包以标准克数(450克)为基准,
超过的克数记作正数,不足的克数记作负数,以下数据是记录
结果,其中表示实际克数最接近标准克数的是( )
A.+2 B.-3
C.+3 D.+4
【解析】选A.通过计算得A为452,B为447,C为453,D为454,
故A最接近标准克数.4.如果盈利10%记为“+10%”,那么亏损6%记为( )
A.-16% B.-6%
C.+6% D.+4%
【解析】选B.根据题意可得:盈利为“+”,则亏损为“-”,
所以亏损6%记为:-6%.5.(2012·连云港中考)某药品说明书上标明药品保存的温度是
(20±2)℃,该药品在_______℃范围内保存才合适.
【解析】温度是20 ℃±2 ℃,表示最低温度是20-2=18(℃),
最高温度是20+2=22(℃),即18~22 ℃之间是合适温度.
答案:18~226.某公交车原有22人,经过3个站点时上下车情况如下(上车为
正,下车为负):(4,-8),(-5,6),(-3,2),求经过3个站
点后车上剩余的人数.
【解析】第一站剩余人数为:22+4-8=18(人);
第二站剩余人数为:18-5+6=19(人);
第三站剩余人数为:19-3+2=18(人).
故最后车上剩余18人.活动二:阅读教材,思考:什么样的数是正数?负数呢?0是正数吗?0是负数吗?什么样的数是有理数?如何对有理数进行分类?探究点二:有理数的概念及其分类合作探究 达成目标【展示点评】正数和负数的概念:
⑴像5,1.2, ,……这样的数叫做 ,它们都比____大;
⑵在正数前面加上“-”号的数叫做 ,如-10,-3等,它们都比____小;
⑶0 既不是 ,也不是 .0是_______和________的分界点,0是____数,也是____数,也是____数.
有理数的概念:整数与分数统称为有理数.有理数的判断方法:①正整数、0、负整数都是有理数.②正分数和负分数都是有理数.【小组讨论2】理解正数和负数时,有什么要注意的问题?对有理数进行分类有哪些标准?如何分?探究点二:有理数的概念及其分类合作探究 达成目标【反思小结】理解正数和负数时,①对于正数和负数的意义,不能简单地理解为带“+”号的数是正数,带“-”号的数是负数.②负数是在正数前面加上一个“-”号,如-5,- (+7)等都是负数,负数中的“-”号不能省略,如-5省略“-”号就是5,变成 正数 了.③0:0既不是正数也不是负数.探究点二:有理数的概念及其分类合作探究 达成目标有理数的分类:正分数负有理数负分数
观察下列各数的特点并分类,填到相应的位置中.
1,2,3,0,-1,-2,-3, , ,5.2, , , -3.5
正整数:______
零:__
负整数:_________
正分数:_________
负分数:___________1,2,30-1,-2,-3例1例2 将下列各数填在相应的大括号内:
5,-2,-0.3, , 0, 5.7, 102, -17
正数:{_________……};
负数:{_________……};
整数:{_________……};
分数:{_________……}.
【总结提升】有理数的分类中的四点注意
1.相对性:正数是相对负数而言的,整数是相对分数而言的.
2.特殊0:0既不是正数,也不是负数,但0是整数.
3.多属性:同一个数,可能属于多个不同的集合.如5既是正数
又是整数.
4.提醒:分数包括有限小数和无限循环小数.练一练:
1.-3.782( )
A.是负数,不是分数
B.不是分数,是有理数
C.是负数,也是分数
D.是分数,不是有理数
【解析】选C.-3.782是负数,也属于分数,还是有理数.2.下列各数:-6,-3.14, ,0,4,-0.2中,整数的个数
为( )
A.2个 B.3个 C.4个 D.5个
【解析】选B.-6是负整数,-3.14是负小数, 是分数,0是
整数,4是整数,-0.2是负小数,所以只有-6,0,4是整数,
所以整数共有3个.3.下列说法正确的个数是( )
① 是负分数;
②1.3不是整数;
③非负有理数不包括0;
④正整数、负整数统称整数;
⑤0是最小的有理数.
A.1个 B.2个 C.3个 D.4个【解析】选B.因为 是负分数,所以①正确;因为1.3是小
数不是整数,所以②正确;因为非负有理数包括0和正有理
数,所以③错误;因为正整数、0、负整数统称为整数,所以
④错误;因为没有最小的有理数,所以0是最小的有理数错
误,即⑤错误.故正确的共有2个.【高手支招】分数和有理数的关系
1.凡是分数都是有理数.
2.有限小数和无限循环小数都可以化为分数,所以是有理数,
不是所有的小数都能表示成分数,如“π”就不能表示成分数.【想一想错在哪?】下面关于“0”的一些说法中正确的是
____________.
①0既不是正数也不是负数;
②0是最小的自然数;
③0是最小的正数;
④0是最小的非负数;
⑤0既不是奇数也不是偶数;
⑥亏损200元,记为-200元,则盈利200元,记为:0元.达标检测 反思目标1. 下列各数中,为负数的是( )
A.0 B.-2 C.1 D.B2. 如果+3吨表示运入仓库的大樱桃吨数,那么运出5吨
大樱桃表示为( )
A.-5吨 B.+5吨 C.-3吨 D.+3吨3. 某项科学研究,以45分钟为1个时间单位,并记每天
上午10时为0,10时以前记为负,10时以后记为正.
例如,9:15记为-1,10:45记为1等等.依此类推
,上午7:45应记为( )
A.-2 B.-2.5 C.-3 D.-7.45AC达标检测 反思目标4. 如果海平面的高度为0米,用负数表示低于海平面的某地的高度,一潜水艇在海平 面 下40米处航行,一条鲨鱼在潜水艇上方10米处游动,那么鲨鱼的高度是________米.5. 把下列各数填入相应的括号内.
1, ,8.9,-2.8,+100, ,-0.03,0,-7
正整数:{ …}
负整数:{ …}
正分数:{ …}
分数:{ …}
自然数:{ …} -30 (打“√”或“×”)
(1)上升5米,记作+5米,则下降5米记作-5米.( )
(2)一个有理数不是正数就是负数.( )
(3)一个有理数不是整数就是分数.( )
(4)负分数一定是负有理数.( )
(5)整数都是正数.( )√×√√×1.用正数和负数表示具有相反意义的量,如气温零上20℃记作:________,盈利3万元记作:________,注意表示时需要带上______.
2.有理数的分类:⑴按符号分类:
⑵按定义分类:
总结梳理 内化目标 +20 ℃ +3万元 单位
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
