八年级数学(上)(北师大版)第三章位置与坐标阶段专题复习课时练(解析版)
文档属性
| 名称 | 八年级数学(上)(北师大版)第三章位置与坐标阶段专题复习课时练(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 260.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-16 20:30:51 | ||
图片预览



文档简介
阶段专题复习
【核心考点训练】
考点一:坐标的确定
1.如图,P1,P2,P3这三个点中,在第二象限内的有 ( )
A.P1,P2,P3
B.P1,P2
C.P1,P3
D.P1
【解析】选D.由图可知,点P1在第二象限,点P2在y轴的正半轴上,点P3在x轴的负半轴上,所以,在第二象限内的有P1.
2.点P在第二象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为 ( )
A.(-4,3)
B.(-3,-4)
C.(-3,4)
D.(3,-4)
【解析】选C.由题意知,点P的横、纵坐标分别为-3,4.
3.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是 ( )
A.(2,0)
B.(4,0)
C.(-2,0)
D.(3,0)
【解析】选D.若点P坐标是(2,0)则OP=AP,△APO是等腰三角形;若点P的坐标是(4,0),则AP=AO,△APO是等腰三角形;若点P的坐标是(-2,0),则OP=OA,△APO是等腰三角形;若点P的坐标是(3,0),则AP≠AO≠OP,△APO不是等腰三角形.
【专家点评】
1.命题角度:本部分内容主要通过各种背景或利用点的特点求点的坐标.
2.解题关键:
确定点的坐标有四种方法:
(1)用定义.由点分别向纵轴和横轴作垂线段,垂足所对应的数就是该点的横、纵坐标.
(2)用距离.点到横、纵轴的距离分别是纵、横坐标的绝对值.
(3)用对称性.用对称性确定点的坐标关键是要把握对称的特点.①关于横轴对称,“纵变横不变”;②关于纵轴对称,“横变纵不变”;③关于原点对称,“纵横都要变”.
(4)由平移、旋转(中心对称)确定点的坐标.
平移要找准平移的方向和距离,将相应坐标进行加减;旋转要结合具体情况,选择恰当方法,按旋转方向及旋转角等,求出相关点的坐标.
考点二:图形的变换
1.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于y轴成轴对称的图形.若点A的坐标是(1,3),则点M和点N的坐标分别是 ( )
A.M(1,-3),N(-1,-3)
B.M(-1,-3),N(-1,3)
C.M(-1,-3),N(1,-3)
D.M(-1,3),N(1,-3)
【解析】选C.因为A,N关于x轴对称,A点的坐标是(1,3),所以N点的坐标是(1,-3),N,M关于y轴对称,N的坐标是(1,-3),所以M点的坐标是(-1,-3).
2.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系.
(2)请画出△ABC关于y轴对称的△A′B′C′.
(3)写出点B′的坐标.
【解析】(答案不唯一)(1)(2)如图,
(3)B′(2,1).
【专家点评】
1.命题角度:本部分内容主要考查变换后的图形的画图及相关计算.
2.解题关键:
(1)此类试题多数都在网格中画图,要找准单位长度,确定好原点.
(2)在确定点的坐标时要充分利用图形的变换方式,得到所求点的坐标是由原来点的坐标如何变换得到的.
考点三:探索规律
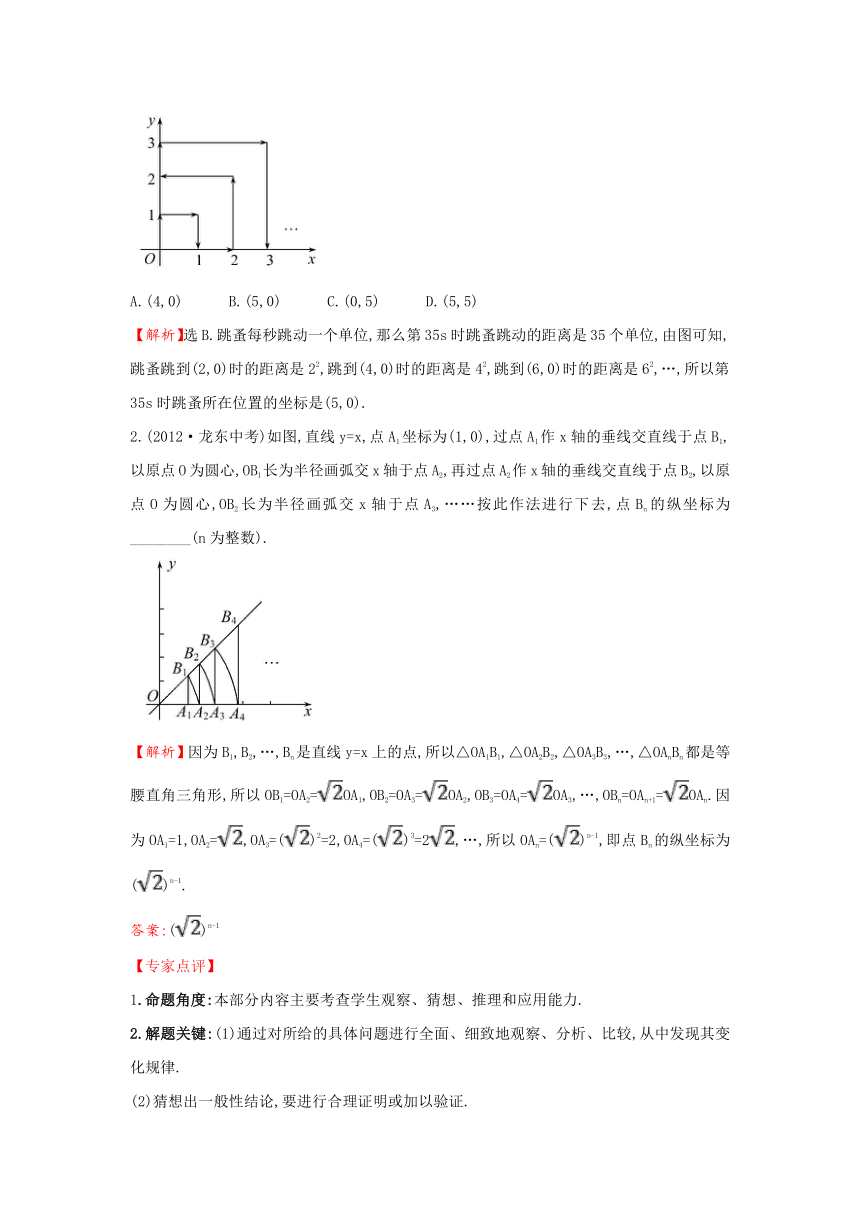
1.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35s时跳蚤所在位置的坐标是 ( )
A.(4,0) B.(5,0) C.(0,5) D.(5,5)
【解析】选B.跳蚤每秒跳动一个单位,那么第35s时跳蚤跳动的距离是35个单位,由图可知,跳蚤跳到(2,0)时的距离是22,跳到(4,0)时的距离是42,跳到(6,0)时的距离是62,…,所以第35s时跳蚤所在位置的坐标是(5,0).
2.(2012·龙东中考)如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,……按此作法进行下去,点Bn的纵坐标为________(n为整数).
【解析】因为B1,B2,…,Bn是直线y=x上的点,所以△OA1B1,△OA2B2,△OA3B3,…,△OAnBn都是等腰直角三角形,所以OB1=OA2=OA1,OB2=OA3=OA2,OB3=OA4=OA3,…,OBn=OAn+1=OAn.因为OA1=1,OA2=,OA3=()2=2,OA4=()3=2,…,所以OAn=()n-1,即点Bn的纵坐标为()n-1.
答案:()n-1
【专家点评】
1.命题角度:本部分内容主要考查学生观察、猜想、推理和应用能力.
2.解题关键:(1)通过对所给的具体问题进行全面、细致地观察、分析、比较,从中发现其变化规律.
(2)猜想出一般性结论,要进行合理证明或加以验证.
【综合训练】
训练点一:坐标的确定
1.(2011·怀化中考)如图,若在象棋盘上建立直角坐标系,使“帥”位于点
(-1,-2),“馬”位于点(2,-2),则“兵”位于点 ( )
A.(-1,1)
B.(-2,-1)
C.(-3,1)
D.(1,-2)
【解析】选C.由已知可知“炮”位于原点,向右、向上为正方向,所以“兵”位于点(-3,1).
2.(2012·西藏中考)平面直角坐标系中,点P的坐标为(-5,3),则点P关于y轴的对称点的坐标是 ( )
A.(5,3)
B.(-5,-3)
C.(3,-5)
D.(-3,5)
【解析】选A.关于y轴对称的点纵坐标相同,横坐标互为相反数,所以点
P(-5,3)关于y轴对称点的坐标是(5,3).
3.(2012·南通中考)线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为 ( )
A.(4,2)
B.(-4,2)
C.(-4,-2)
D.(4,-2)
【解析】选D.根据直角坐标系可得M点坐标是(-4,-2),故点M的对应点M′的坐标为(4,-2).
训练点二:图形的变换
4.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的坐标为 ( )
A.(2,0)
B.(-1,0)
C.(-1,0)
D.(,0)
【解析】选C.在Rt△ABC中,由勾股定理得,
AC===,
所以AM=AC=,所以BM=AM-AB=-3,
又因为点B的坐标为(2,0),
所以点M的坐标为(2+-3,0),即(-1,0).
5.甲、乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下
子,黑棋下子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个
棋子也成轴对称图形.则下列下子方法不正确的是 ( )
[说明:棋子的位置用数对表示,如A点在(6,3)]
A.黑(3,7),白(5,3)
B.黑(4,7),白(6,2)
C.黑(2,7),白(5,3)
D.黑(3,7),白(2,6)
【解析】选C.若放入黑(3,7),白(5,3),则此时黑棋组成轴对称图形,白棋也组成轴对称图形,故A选项错误;若放入黑(4,7),白(6,2),则此时黑棋组成轴对称图形,白棋也组成轴对称图形,故B选项错误;若放入黑(2,7),白(5,3),则此时黑棋不能组成轴对称图形,白棋组成轴对称图形,故C选项正确;若放入黑(3,7),白(2,6),则此时黑棋组成轴对称图形,白棋也组成轴对称图形,故D选项错误.
训练点三:探索规律
6.如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),
D(1,-2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是 ( )
A.(1,-1)
B.(-1,1)
C.(-1,-2)
D.(1,-2)
【解析】选B.长方形ABCD的周长为10,2012÷10=201……2,说明细线绕了
201圈,回到A点后又继续绕了2个单位,故到达B点.
7.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,
△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为____________.
【解析】因为2012是4的倍数,
所以A1﹣﹣A4;A5﹣﹣A8;…每4个为一组,
所以A2012在x轴上方,横坐标为2,
因为A4,A8,A12的纵坐标分别为2,4,6,
所以A2012的纵坐标为2012×=1006.
答案:(2,1006)
8.如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2012的坐标为________.
【解析】根据题意点B1的坐标为(0,2),即(0,21);再以对角线OB1为边作第三个
正方形OB1B2C2,则点B2的坐标为(-2,2),即(-21,21);同理可分别求得点
B3(-22,0),B4(-22,-22),B5(0,-23),B6(23,-23),B7(24,0),B8(24,24),B9(0,25),…,可以看出8个点一循环,2012÷8=251…4,第4点在第三象限,横、纵坐标均为负,且2的指数为点B下标的一半,所以点B2012的坐标为B2012(-21006,-21006).
答案:(-21006,-21006).
【核心考点训练】
考点一:坐标的确定
1.如图,P1,P2,P3这三个点中,在第二象限内的有 ( )
A.P1,P2,P3
B.P1,P2
C.P1,P3
D.P1
【解析】选D.由图可知,点P1在第二象限,点P2在y轴的正半轴上,点P3在x轴的负半轴上,所以,在第二象限内的有P1.
2.点P在第二象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为 ( )
A.(-4,3)
B.(-3,-4)
C.(-3,4)
D.(3,-4)
【解析】选C.由题意知,点P的横、纵坐标分别为-3,4.
3.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是 ( )
A.(2,0)
B.(4,0)
C.(-2,0)
D.(3,0)
【解析】选D.若点P坐标是(2,0)则OP=AP,△APO是等腰三角形;若点P的坐标是(4,0),则AP=AO,△APO是等腰三角形;若点P的坐标是(-2,0),则OP=OA,△APO是等腰三角形;若点P的坐标是(3,0),则AP≠AO≠OP,△APO不是等腰三角形.
【专家点评】
1.命题角度:本部分内容主要通过各种背景或利用点的特点求点的坐标.
2.解题关键:
确定点的坐标有四种方法:
(1)用定义.由点分别向纵轴和横轴作垂线段,垂足所对应的数就是该点的横、纵坐标.
(2)用距离.点到横、纵轴的距离分别是纵、横坐标的绝对值.
(3)用对称性.用对称性确定点的坐标关键是要把握对称的特点.①关于横轴对称,“纵变横不变”;②关于纵轴对称,“横变纵不变”;③关于原点对称,“纵横都要变”.
(4)由平移、旋转(中心对称)确定点的坐标.
平移要找准平移的方向和距离,将相应坐标进行加减;旋转要结合具体情况,选择恰当方法,按旋转方向及旋转角等,求出相关点的坐标.
考点二:图形的变换
1.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于y轴成轴对称的图形.若点A的坐标是(1,3),则点M和点N的坐标分别是 ( )
A.M(1,-3),N(-1,-3)
B.M(-1,-3),N(-1,3)
C.M(-1,-3),N(1,-3)
D.M(-1,3),N(1,-3)
【解析】选C.因为A,N关于x轴对称,A点的坐标是(1,3),所以N点的坐标是(1,-3),N,M关于y轴对称,N的坐标是(1,-3),所以M点的坐标是(-1,-3).
2.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系.
(2)请画出△ABC关于y轴对称的△A′B′C′.
(3)写出点B′的坐标.
【解析】(答案不唯一)(1)(2)如图,
(3)B′(2,1).
【专家点评】
1.命题角度:本部分内容主要考查变换后的图形的画图及相关计算.
2.解题关键:
(1)此类试题多数都在网格中画图,要找准单位长度,确定好原点.
(2)在确定点的坐标时要充分利用图形的变换方式,得到所求点的坐标是由原来点的坐标如何变换得到的.
考点三:探索规律
1.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35s时跳蚤所在位置的坐标是 ( )
A.(4,0) B.(5,0) C.(0,5) D.(5,5)
【解析】选B.跳蚤每秒跳动一个单位,那么第35s时跳蚤跳动的距离是35个单位,由图可知,跳蚤跳到(2,0)时的距离是22,跳到(4,0)时的距离是42,跳到(6,0)时的距离是62,…,所以第35s时跳蚤所在位置的坐标是(5,0).
2.(2012·龙东中考)如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2,再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,……按此作法进行下去,点Bn的纵坐标为________(n为整数).
【解析】因为B1,B2,…,Bn是直线y=x上的点,所以△OA1B1,△OA2B2,△OA3B3,…,△OAnBn都是等腰直角三角形,所以OB1=OA2=OA1,OB2=OA3=OA2,OB3=OA4=OA3,…,OBn=OAn+1=OAn.因为OA1=1,OA2=,OA3=()2=2,OA4=()3=2,…,所以OAn=()n-1,即点Bn的纵坐标为()n-1.
答案:()n-1
【专家点评】
1.命题角度:本部分内容主要考查学生观察、猜想、推理和应用能力.
2.解题关键:(1)通过对所给的具体问题进行全面、细致地观察、分析、比较,从中发现其变化规律.
(2)猜想出一般性结论,要进行合理证明或加以验证.
【综合训练】
训练点一:坐标的确定
1.(2011·怀化中考)如图,若在象棋盘上建立直角坐标系,使“帥”位于点
(-1,-2),“馬”位于点(2,-2),则“兵”位于点 ( )
A.(-1,1)
B.(-2,-1)
C.(-3,1)
D.(1,-2)
【解析】选C.由已知可知“炮”位于原点,向右、向上为正方向,所以“兵”位于点(-3,1).
2.(2012·西藏中考)平面直角坐标系中,点P的坐标为(-5,3),则点P关于y轴的对称点的坐标是 ( )
A.(5,3)
B.(-5,-3)
C.(3,-5)
D.(-3,5)
【解析】选A.关于y轴对称的点纵坐标相同,横坐标互为相反数,所以点
P(-5,3)关于y轴对称点的坐标是(5,3).
3.(2012·南通中考)线段MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应的点M1的坐标为 ( )
A.(4,2)
B.(-4,2)
C.(-4,-2)
D.(4,-2)
【解析】选D.根据直角坐标系可得M点坐标是(-4,-2),故点M的对应点M′的坐标为(4,-2).
训练点二:图形的变换
4.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的坐标为 ( )
A.(2,0)
B.(-1,0)
C.(-1,0)
D.(,0)
【解析】选C.在Rt△ABC中,由勾股定理得,
AC===,
所以AM=AC=,所以BM=AM-AB=-3,
又因为点B的坐标为(2,0),
所以点M的坐标为(2+-3,0),即(-1,0).
5.甲、乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下
子,黑棋下子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个
棋子也成轴对称图形.则下列下子方法不正确的是 ( )
[说明:棋子的位置用数对表示,如A点在(6,3)]
A.黑(3,7),白(5,3)
B.黑(4,7),白(6,2)
C.黑(2,7),白(5,3)
D.黑(3,7),白(2,6)
【解析】选C.若放入黑(3,7),白(5,3),则此时黑棋组成轴对称图形,白棋也组成轴对称图形,故A选项错误;若放入黑(4,7),白(6,2),则此时黑棋组成轴对称图形,白棋也组成轴对称图形,故B选项错误;若放入黑(2,7),白(5,3),则此时黑棋不能组成轴对称图形,白棋组成轴对称图形,故C选项正确;若放入黑(3,7),白(2,6),则此时黑棋组成轴对称图形,白棋也组成轴对称图形,故D选项错误.
训练点三:探索规律
6.如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),
D(1,-2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是 ( )
A.(1,-1)
B.(-1,1)
C.(-1,-2)
D.(1,-2)
【解析】选B.长方形ABCD的周长为10,2012÷10=201……2,说明细线绕了
201圈,回到A点后又继续绕了2个单位,故到达B点.
7.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,
△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为____________.
【解析】因为2012是4的倍数,
所以A1﹣﹣A4;A5﹣﹣A8;…每4个为一组,
所以A2012在x轴上方,横坐标为2,
因为A4,A8,A12的纵坐标分别为2,4,6,
所以A2012的纵坐标为2012×=1006.
答案:(2,1006)
8.如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2012的坐标为________.
【解析】根据题意点B1的坐标为(0,2),即(0,21);再以对角线OB1为边作第三个
正方形OB1B2C2,则点B2的坐标为(-2,2),即(-21,21);同理可分别求得点
B3(-22,0),B4(-22,-22),B5(0,-23),B6(23,-23),B7(24,0),B8(24,24),B9(0,25),…,可以看出8个点一循环,2012÷8=251…4,第4点在第三象限,横、纵坐标均为负,且2的指数为点B下标的一半,所以点B2012的坐标为B2012(-21006,-21006).
答案:(-21006,-21006).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
