七年级数学(上)(北师大版)第一章丰富多彩的图形世界2展开与折叠课时练(解析版)
文档属性
| 名称 | 七年级数学(上)(北师大版)第一章丰富多彩的图形世界2展开与折叠课时练(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 207.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-16 22:24:52 | ||
图片预览


文档简介
2展开与折叠
【教材训练】5分钟
1.几种常见的几何体展开图
(1)将正方体沿某些棱剪开可得到11种不同的平面图形.
(2)棱柱的展开图是由两个边数相同(填“相同”或“不相同”)的多边形和一些长方形组成的,沿棱柱表面的不同棱剪开,得到的展开图也可能不同.
(3)圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形.
2.几种常见几何体的截面形状
几何体
截面形状
正方体
三角形、四边形、五边形、六边形
圆柱
长方形、圆、椭圆、不规则图形
圆锥
三角形、圆、椭圆、不规则图形
3.判断训练(打“√”或“×”)
(1)同一种几何体的表面展开图只能有一种形式. (×)
(2)正方体的展开图中不能含有“田”字型图形. (√)
(3)任意几何体的截面都不止一种图形. (×)
(4)只有正方体的截面可能是正方形. (×)
【课堂达标】20分钟
训练点一:几何体的展开与折叠
1.(2分)下列图形中为正方体的平面展开图的是 ( )
【解析】选C.由四棱柱四个侧面和上下两个底面的特征可知,A,B,D上底面不可能有两个,故不是正方体的展开图.选项C可以拼成一个正方体.
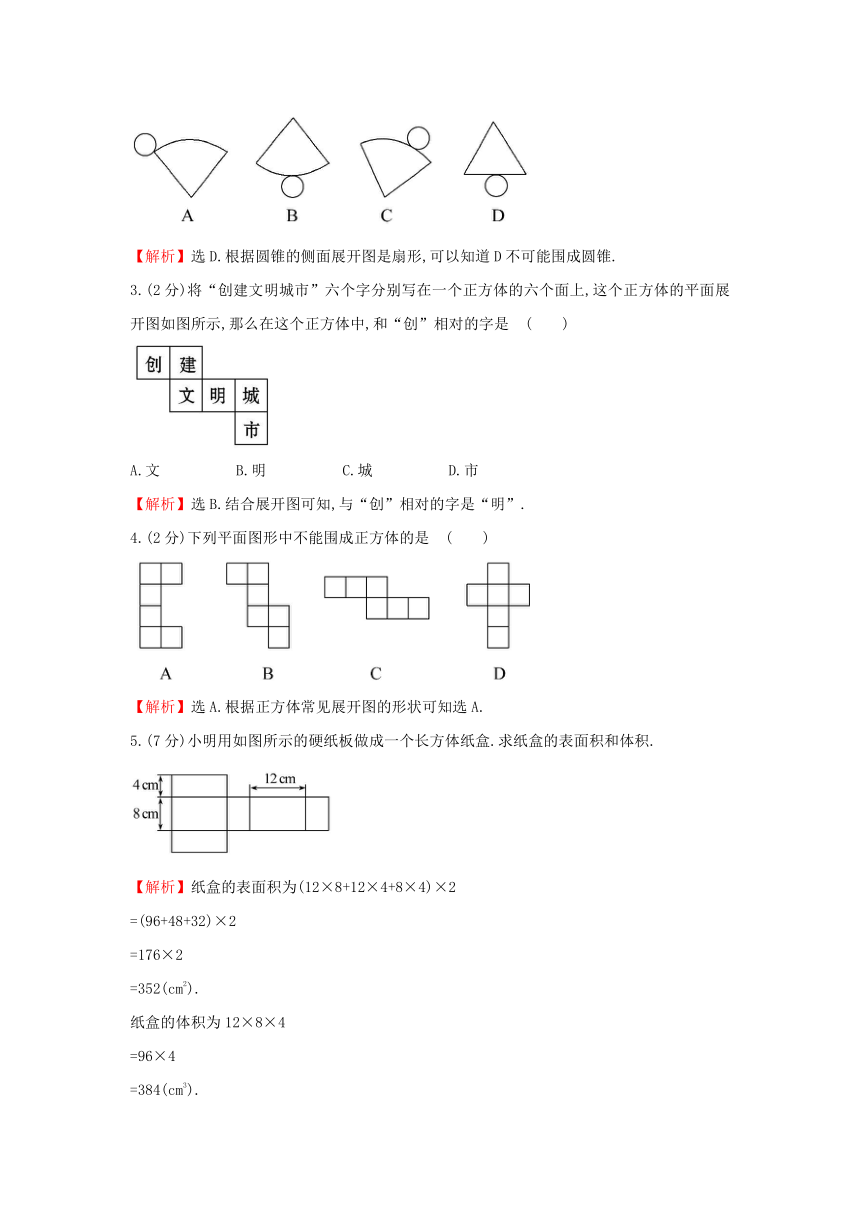
2.(2分)如图所示的平面图形中,不可能围成圆锥的是 ( )
【解析】选D.根据圆锥的侧面展开图是扇形,可以知道D不可能围成圆锥.
3.(2分)将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是 ( )
A.文 B.明 C.城 D.市
【解析】选B.结合展开图可知,与“创”相对的字是“明”.
4.(2分)下列平面图形中不能围成正方体的是 ( )
【解析】选A.根据正方体常见展开图的形状可知选A.
5.(7分)小明用如图所示的硬纸板做成一个长方体纸盒.求纸盒的表面积和体积.
【解析】纸盒的表面积为(12×8+12×4+8×4)×2
=(96+48+32)×2
=176×2
=352(cm2).
纸盒的体积为12×8×4
=96×4
=384(cm3).
答:纸盒的表面积是352cm2,体积是384cm3.
训练点二:截面
1.(2分)用一个平面去截一个几何体,不能截得三角形截面的几何体是 ( )
A.圆柱 B.圆锥 C.三棱柱 D.正方体
【解析】选A.圆柱的截面可能是圆、椭圆、长方形和一些不规则图形,不能截得三角形.
2.(2分)用一个平面去截一个正方体,则截面的形状不可能为 ( )
A.四边形 B.七边形 C.六边形 D.三角形
【解析】选B.正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此不可能是七边形.
3.(2分)如图,用平面去截圆锥,所得截面的形状是 ( )
【解析】选D.由题中图知截面是D.
4.(3分)用一个平面去截五棱柱,则截面不可能是________.
①三角形;②四边形;③五边形;④圆(将符合题意的序号填上即可).
【解析】当截面分别经过三个面,四个面,五个面时,得到的截面的形状分别是三角形,四边形,五边形,截面不可能是圆.
答案:④
5.(6分)(1)找出三种几何体,分别用一个平面去截它们,可以得到圆形的截面.
(2)找出三种几何体,分别用一个平面去截它们,可以得到三角形的截面.
【解析】(1)圆柱、圆锥、球.(2)正方体、三棱柱、圆锥.
【课后作业】30分钟
一、选择题(每小题4分,共12分)
1.一个几何体的展开图如图所示,这个几何体是 ( )
A.三棱柱 B.三棱锥 C.四棱柱 D.四棱锥
【解析】选A.该几何体底面为一个三角形,由三条棱组成,故该几何体为三棱柱.
2.如图是一个正方体的平面展开图,原正方体中“祝”的对面是 ( )
A.考 B.试 C.顺 D.利
【解析】选C.把上面的“祝”字向外折叠,把下面的“顺”字向外折叠,与上面的“祝”字形成对面,再把左边的“考”向外折叠后,把“你”向里折叠,“考”作左侧面,“你”作为前侧面,“利”作为右侧面.显然,“祝”与“顺”形成对面.
3.如图是正方体切割后剩下的部分,它的另一部分为 ( )
【解析】选B.将原图形顺时针旋转90°,将原图形实线改虚线,虚线改实线,可知变换后的图形与选项B相符.
二、填空题(每小题4分,共12分)
4.用一个平面去截一个几何体,若截出的面是四边形,那么这个几何体可能是________.(至少填三种不同的几何体)
【解析】长方体、正方体、圆柱、四棱柱、五棱柱等截面都可能是四边形.
答案:长方体、正方体、圆柱(答案不惟一)
5.如图,把一个棱长为2的立方体截成八个棱长为1的小立方块,至少需截________次.
【解析】如图所示至少需截3次.
答案:3
6.如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等,则这六个数的和为______.
【解析】从4,5,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8或4,5,6,7,8,9,因为相对面上的数字和相等,所以第一种情况必须是4,5处于对面,第二种情况必须是4,7处于对面,故这六个数字只能是4,5,6,7,8,9,所以这六个数的和为4+5+6+7+8+9=39.
答案:39
三、解答题(共26分)
7.(6分)如图,下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应连线.
【解析】连线如下图:
8.(6分)教师节之前,马小虎同学亲手为老师制作了一件手工艺品,并设计了一个包装盒,由于粗心,在设计图上少设计了一块正方形纸块.请你在图上画出三种设计图,使其能成为一个有盖的正方体盒子.
【解析】如图所示:
9.(6分)已知:如图所示无盖纸盒的长宽高都是10cm.
(1)画出纸盒的一种平面展开图.
(2)计算纸盒所用材料的面积.
【解析】(1)如图所示:(答案不惟一)
(2)纸盒所用材料的面积=5×102=5×100=500(cm2).
答:纸盒所用材料的面积为500cm2.
10.(8分)(能力拔高题)如果用一平面截掉一个正方体的一个角,剩下的几何体有几个顶点?几条棱?几个面?
【解析】分如下四种情况:(1)不过顶点.如图①所示,截面为三角形,剩下的几何体的顶点有8-1+3=10(个);棱有12+3=15(条);面有6+1=7(个).
① ② ③ ④
(2)过一个顶点.如图②所示,截面为三角形,剩下的几何体的顶点有
8-1+2=9(个);棱有12-1+3=14(条);面有6+1=7(个).
(3)过两个顶点.如图③所示,截面为三角形,剩下的几何体的顶点有
8-1+1=8(个);棱有12-2+3=13(条);面有6+1=7(个).
(4)过三个顶点.如图④所示,截面为三角形,剩下的几何体的顶点有8-1=7(个);棱有12-3+3=12(条);面有6+1=7(个).
【教材训练】5分钟
1.几种常见的几何体展开图
(1)将正方体沿某些棱剪开可得到11种不同的平面图形.
(2)棱柱的展开图是由两个边数相同(填“相同”或“不相同”)的多边形和一些长方形组成的,沿棱柱表面的不同棱剪开,得到的展开图也可能不同.
(3)圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形.
2.几种常见几何体的截面形状
几何体
截面形状
正方体
三角形、四边形、五边形、六边形
圆柱
长方形、圆、椭圆、不规则图形
圆锥
三角形、圆、椭圆、不规则图形
3.判断训练(打“√”或“×”)
(1)同一种几何体的表面展开图只能有一种形式. (×)
(2)正方体的展开图中不能含有“田”字型图形. (√)
(3)任意几何体的截面都不止一种图形. (×)
(4)只有正方体的截面可能是正方形. (×)
【课堂达标】20分钟
训练点一:几何体的展开与折叠
1.(2分)下列图形中为正方体的平面展开图的是 ( )
【解析】选C.由四棱柱四个侧面和上下两个底面的特征可知,A,B,D上底面不可能有两个,故不是正方体的展开图.选项C可以拼成一个正方体.
2.(2分)如图所示的平面图形中,不可能围成圆锥的是 ( )
【解析】选D.根据圆锥的侧面展开图是扇形,可以知道D不可能围成圆锥.
3.(2分)将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是 ( )
A.文 B.明 C.城 D.市
【解析】选B.结合展开图可知,与“创”相对的字是“明”.
4.(2分)下列平面图形中不能围成正方体的是 ( )
【解析】选A.根据正方体常见展开图的形状可知选A.
5.(7分)小明用如图所示的硬纸板做成一个长方体纸盒.求纸盒的表面积和体积.
【解析】纸盒的表面积为(12×8+12×4+8×4)×2
=(96+48+32)×2
=176×2
=352(cm2).
纸盒的体积为12×8×4
=96×4
=384(cm3).
答:纸盒的表面积是352cm2,体积是384cm3.
训练点二:截面
1.(2分)用一个平面去截一个几何体,不能截得三角形截面的几何体是 ( )
A.圆柱 B.圆锥 C.三棱柱 D.正方体
【解析】选A.圆柱的截面可能是圆、椭圆、长方形和一些不规则图形,不能截得三角形.
2.(2分)用一个平面去截一个正方体,则截面的形状不可能为 ( )
A.四边形 B.七边形 C.六边形 D.三角形
【解析】选B.正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此不可能是七边形.
3.(2分)如图,用平面去截圆锥,所得截面的形状是 ( )
【解析】选D.由题中图知截面是D.
4.(3分)用一个平面去截五棱柱,则截面不可能是________.
①三角形;②四边形;③五边形;④圆(将符合题意的序号填上即可).
【解析】当截面分别经过三个面,四个面,五个面时,得到的截面的形状分别是三角形,四边形,五边形,截面不可能是圆.
答案:④
5.(6分)(1)找出三种几何体,分别用一个平面去截它们,可以得到圆形的截面.
(2)找出三种几何体,分别用一个平面去截它们,可以得到三角形的截面.
【解析】(1)圆柱、圆锥、球.(2)正方体、三棱柱、圆锥.
【课后作业】30分钟
一、选择题(每小题4分,共12分)
1.一个几何体的展开图如图所示,这个几何体是 ( )
A.三棱柱 B.三棱锥 C.四棱柱 D.四棱锥
【解析】选A.该几何体底面为一个三角形,由三条棱组成,故该几何体为三棱柱.
2.如图是一个正方体的平面展开图,原正方体中“祝”的对面是 ( )
A.考 B.试 C.顺 D.利
【解析】选C.把上面的“祝”字向外折叠,把下面的“顺”字向外折叠,与上面的“祝”字形成对面,再把左边的“考”向外折叠后,把“你”向里折叠,“考”作左侧面,“你”作为前侧面,“利”作为右侧面.显然,“祝”与“顺”形成对面.
3.如图是正方体切割后剩下的部分,它的另一部分为 ( )
【解析】选B.将原图形顺时针旋转90°,将原图形实线改虚线,虚线改实线,可知变换后的图形与选项B相符.
二、填空题(每小题4分,共12分)
4.用一个平面去截一个几何体,若截出的面是四边形,那么这个几何体可能是________.(至少填三种不同的几何体)
【解析】长方体、正方体、圆柱、四棱柱、五棱柱等截面都可能是四边形.
答案:长方体、正方体、圆柱(答案不惟一)
5.如图,把一个棱长为2的立方体截成八个棱长为1的小立方块,至少需截________次.
【解析】如图所示至少需截3次.
答案:3
6.如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等,则这六个数的和为______.
【解析】从4,5,7三个数字看出可能是2,3,4,5,6,7或3,4,5,6,7,8或4,5,6,7,8,9,因为相对面上的数字和相等,所以第一种情况必须是4,5处于对面,第二种情况必须是4,7处于对面,故这六个数字只能是4,5,6,7,8,9,所以这六个数的和为4+5+6+7+8+9=39.
答案:39
三、解答题(共26分)
7.(6分)如图,下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应连线.
【解析】连线如下图:
8.(6分)教师节之前,马小虎同学亲手为老师制作了一件手工艺品,并设计了一个包装盒,由于粗心,在设计图上少设计了一块正方形纸块.请你在图上画出三种设计图,使其能成为一个有盖的正方体盒子.
【解析】如图所示:
9.(6分)已知:如图所示无盖纸盒的长宽高都是10cm.
(1)画出纸盒的一种平面展开图.
(2)计算纸盒所用材料的面积.
【解析】(1)如图所示:(答案不惟一)
(2)纸盒所用材料的面积=5×102=5×100=500(cm2).
答:纸盒所用材料的面积为500cm2.
10.(8分)(能力拔高题)如果用一平面截掉一个正方体的一个角,剩下的几何体有几个顶点?几条棱?几个面?
【解析】分如下四种情况:(1)不过顶点.如图①所示,截面为三角形,剩下的几何体的顶点有8-1+3=10(个);棱有12+3=15(条);面有6+1=7(个).
① ② ③ ④
(2)过一个顶点.如图②所示,截面为三角形,剩下的几何体的顶点有
8-1+2=9(个);棱有12-1+3=14(条);面有6+1=7(个).
(3)过两个顶点.如图③所示,截面为三角形,剩下的几何体的顶点有
8-1+1=8(个);棱有12-2+3=13(条);面有6+1=7(个).
(4)过三个顶点.如图④所示,截面为三角形,剩下的几何体的顶点有8-1=7(个);棱有12-3+3=12(条);面有6+1=7(个).
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
