2016年秋人教版九年级数学上册教学课件:23.1 图形的旋转 (共12张PPT)
文档属性
| 名称 | 2016年秋人教版九年级数学上册教学课件:23.1 图形的旋转 (共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 174.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-17 00:00:00 | ||
图片预览





文档简介
课件12张PPT。生活中的旋转(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α(即把图形F上的每一个点与定点的连线绕定点O旋转角α),图形的这种变换叫做旋转(cricumrotate),这个定点O叫旋转中心,角α叫做旋转角。原位置的图形F叫做原像,新位置的图形F'叫做图形F在旋转下的像。图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点。议一议:
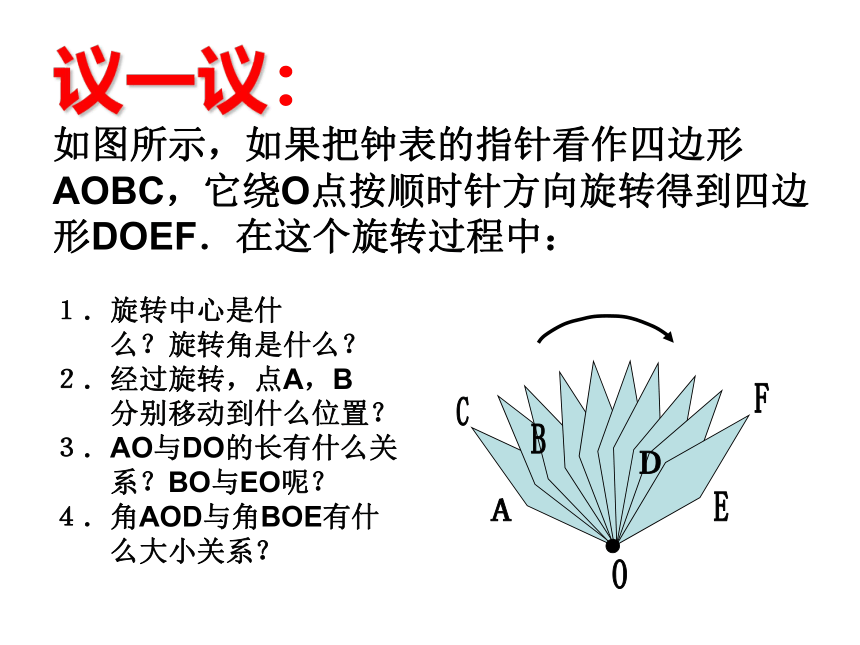
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什
么?旋转角是什么?
2.经过旋转,点A,B
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4.角AOD与角BOE有什
么大小关系?BACODEF 旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)两组对应点分别与旋转中心的连
线所成的角相等,且等于旋转角.
(4)对应点到旋转中心的距离相等.例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?解:
(1)它的旋转中心是钟表
的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGH随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?再见
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α(即把图形F上的每一个点与定点的连线绕定点O旋转角α),图形的这种变换叫做旋转(cricumrotate),这个定点O叫旋转中心,角α叫做旋转角。原位置的图形F叫做原像,新位置的图形F'叫做图形F在旋转下的像。图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点。议一议:
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什
么?旋转角是什么?
2.经过旋转,点A,B
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4.角AOD与角BOE有什
么大小关系?BACODEF 旋转的基本性质
(1)旋转不改变图形的大小和形状.
(2)图形上的每一点都绕旋转中心沿
相同方向转动了相同的角度.
(3)两组对应点分别与旋转中心的连
线所成的角相等,且等于旋转角.
(4)对应点到旋转中心的距离相等.例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?解:
(1)它的旋转中心是钟表
的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为做一做:
在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.ACBDEFGH随堂练习:
本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?再见
同课章节目录
