数学:3.1.2《用二分法求方程的近似解(三)》课件(新人教a版必修1)
文档属性
| 名称 | 数学:3.1.2《用二分法求方程的近似解(三)》课件(新人教a版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 256.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-03 14:28:00 | ||
图片预览





文档简介
课件15张PPT。用二分法求方程的近似解 数学是锻炼思维的体操
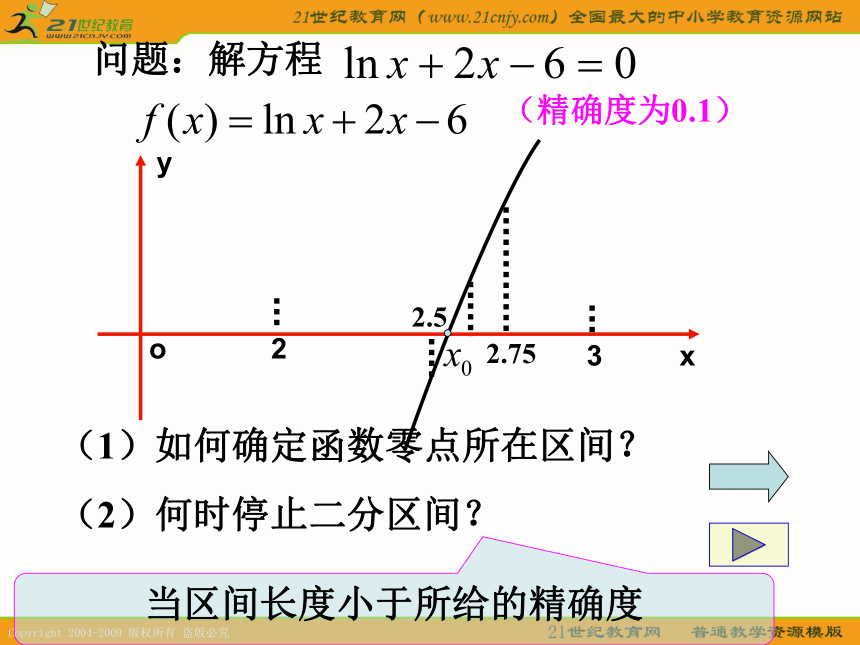
——加里宁如果函数连续不断的一条曲线,并且 f(a)·f(b)<0那么 有零点,即存在 复习引入:1.2.问题:解方程(2)何时停止二分区间?当区间长度小于所给的精确度(精确度为0.1)(1)如何确定函数零点所在区间?I、二分法的定义:对于在区间[a,b]上连续不断且 的函数 y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法. 思考:是否所有存在零点的函数都可以用二分法求得零点?-0.08(-)2.5中点的函数近似值(符号)中点的值区间(a,b)(2.5,2.5625)0.07(+)2.5625(2.5,2.625)0.22(+)2.625(2.5,2.75)0.51(+)2.75(2.5,3)(2,3)4、判断是否达到精确度 :
若新区间的区间长度(两端点之差的绝对值)小于 ,则达到了精确度,取区间端点之一为零点的近似值即告结束;否则,重复2-4的工作。II、给定精确度ε,用二分法求函数f(x)零点近似值的步骤:1、选取满足条件 的实数(一般取整数)a,b , 确定区间[a,b];2、求区间(a,b)的中点 ,记为c ;3、计算f(c),并进行判断:
(1)若f(c) =0,则c 就是函数的零点,结束;
(2)若 ,则 ,令b=c,转向4;
(3)若 ,则 ,令a=c,转向4;
例1、借助计算器或计算机用二分法求方程
的近似解(精确度0.1) 取区间(1,2)的中点 ,得
再取(1,1.5)的中点 ,得
同理可得,
由于
所以,原方程的近似解可取为1.4375.解:原方程即 ,令
作出函数 的对应值,得从而 ,故函数在区间(1,2)内有零点(1.375,1.4375)0.02(+)1.4375(1.375,1.5)-0.28(-)1.375(1.25,1.5)-0.87(-)1.25(1,1.5)0.33(+)1.5(1,2)中点函数的近似值(符号)中点值区间(a,b)利用二分法可列下表:一、二、 下列函数图象与x轴均有交点,其中不能用二分法求图中函数零点的图号是( )经典练习: 借助计算器,用二分法求方程 在区间(2,3)内的近似解(精确度为0.1)解:原方程即 ,令
用计算器可算得
从而 得这个方程在区间(2,3)内有一个解。
取区间(2,3)的中点 ,可得
再取区间(2.5,3)的中点 ,可得
同理可得
由于
所以原方程的近似解可取为2.5625. 某方程有一根在区间(0,1)之内,若用二
分法求此根的近似值,使用“二分法”n次后,
区间长度为?要求精确度为0.1,则至多将要
等分的次数为?若区间改为(a,b)呢?探究1、本节内容:(1)“二分法”的定义;(2)给定精确度,用“二分法”求函数零点近似
值的步骤。学后总结:1、教材100页第1题;
2、教材102页B组第1题作业:
——加里宁如果函数连续不断的一条曲线,并且 f(a)·f(b)<0那么 有零点,即存在 复习引入:1.2.问题:解方程(2)何时停止二分区间?当区间长度小于所给的精确度(精确度为0.1)(1)如何确定函数零点所在区间?I、二分法的定义:对于在区间[a,b]上连续不断且 的函数 y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法. 思考:是否所有存在零点的函数都可以用二分法求得零点?-0.08(-)2.5中点的函数近似值(符号)中点的值区间(a,b)(2.5,2.5625)0.07(+)2.5625(2.5,2.625)0.22(+)2.625(2.5,2.75)0.51(+)2.75(2.5,3)(2,3)4、判断是否达到精确度 :
若新区间的区间长度(两端点之差的绝对值)小于 ,则达到了精确度,取区间端点之一为零点的近似值即告结束;否则,重复2-4的工作。II、给定精确度ε,用二分法求函数f(x)零点近似值的步骤:1、选取满足条件 的实数(一般取整数)a,b , 确定区间[a,b];2、求区间(a,b)的中点 ,记为c ;3、计算f(c),并进行判断:
(1)若f(c) =0,则c 就是函数的零点,结束;
(2)若 ,则 ,令b=c,转向4;
(3)若 ,则 ,令a=c,转向4;
例1、借助计算器或计算机用二分法求方程
的近似解(精确度0.1) 取区间(1,2)的中点 ,得
再取(1,1.5)的中点 ,得
同理可得,
由于
所以,原方程的近似解可取为1.4375.解:原方程即 ,令
作出函数 的对应值,得从而 ,故函数在区间(1,2)内有零点(1.375,1.4375)0.02(+)1.4375(1.375,1.5)-0.28(-)1.375(1.25,1.5)-0.87(-)1.25(1,1.5)0.33(+)1.5(1,2)中点函数的近似值(符号)中点值区间(a,b)利用二分法可列下表:一、二、 下列函数图象与x轴均有交点,其中不能用二分法求图中函数零点的图号是( )经典练习: 借助计算器,用二分法求方程 在区间(2,3)内的近似解(精确度为0.1)解:原方程即 ,令
用计算器可算得
从而 得这个方程在区间(2,3)内有一个解。
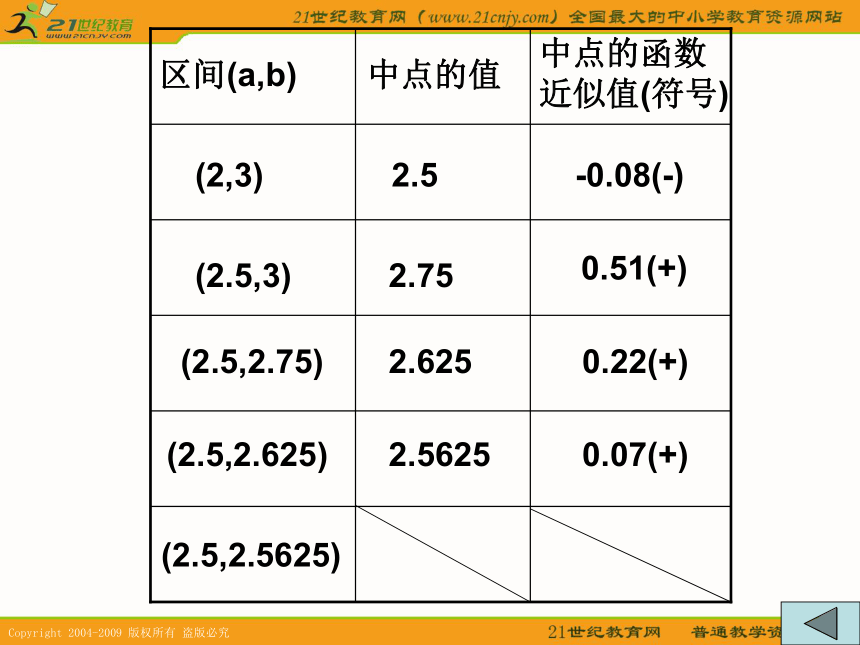
取区间(2,3)的中点 ,可得
再取区间(2.5,3)的中点 ,可得
同理可得
由于
所以原方程的近似解可取为2.5625. 某方程有一根在区间(0,1)之内,若用二
分法求此根的近似值,使用“二分法”n次后,
区间长度为?要求精确度为0.1,则至多将要
等分的次数为?若区间改为(a,b)呢?探究1、本节内容:(1)“二分法”的定义;(2)给定精确度,用“二分法”求函数零点近似
值的步骤。学后总结:1、教材100页第1题;
2、教材102页B组第1题作业:
