数学:3.1.2《用二分法求方程的近似解(四)》课件(新人教a版必修1)
文档属性
| 名称 | 数学:3.1.2《用二分法求方程的近似解(四)》课件(新人教a版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 343.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-03 14:28:00 | ||
图片预览




文档简介
课件10张PPT。用二分法求方程的近似解在八个大小形状完全一样的银元中有一个是假银元,
已知假银元比真银元稍轻点儿。现在只有一个天平,
如何找出假银元?思考,探究, 发现一元二次方程可以用公式求根,
如何求方程lnx+2x-6=0的根呢?找函数
f(x)=lnx+2x-6
的零点.f(x)=lnx+2x-6-10 -5 5 10 ↓↓↓yx0转化方程f(x)=0有根等价于______________函数y=f(x)有零点求方程的根就是______________
找对应函数的零点函数y=f(x)的图象在区间[a,b]上是一条
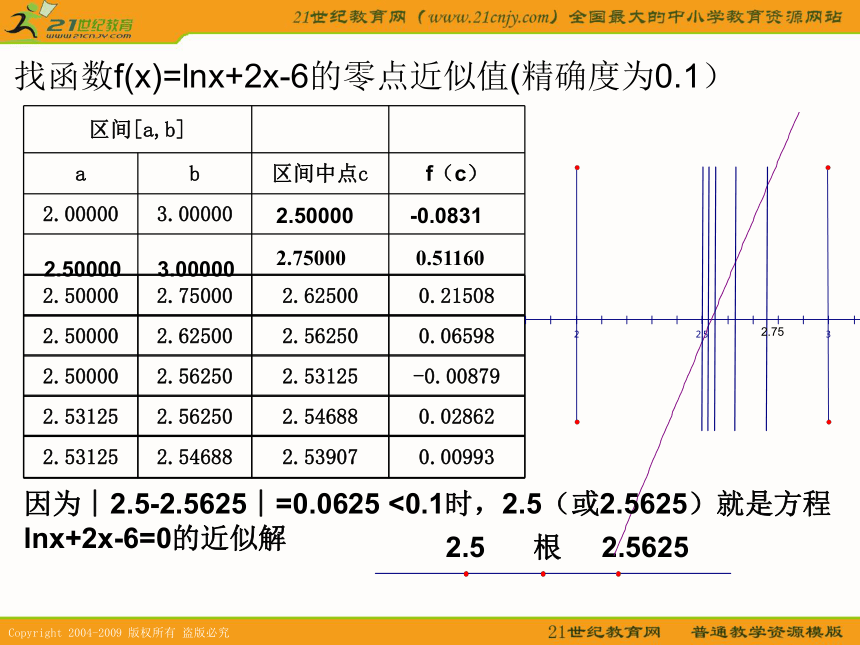
___________的曲线,且___________,则函数在区间(a,b)上有零点。 f(a)?f(b)<0时连续不断 2.50000 -0.0831 2.50000 3.000002.5 根 2.5625找函数f(x)=lnx+2x-6的零点近似值(精确度为0.1)2.75因为︱2.5-2.5625︱=0.0625 <0.1时,2.5(或2.5625)就是方程lnx+2x-6=0的近似解2.75000 0.51160二分法定义:
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数
y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,
使区间的两个端点逐步逼近零点,进而得到零点近似值的方
法叫做二分法 .______________归纳:用二分法求函数f(x)零点近似值的步骤: 1.确定区间[a,b],验证f(a )·f(b)﹤0,给定精确度m;2.求区间(a,b)的中点c;3.计算f(c);4.判断是否达到精确度;若︱ a-b︱﹤m则得到零点
近似值a(或b);否则重复2~4。(1)若f(c)=0,(2)若f(a)·f(c)﹤0,(3)若f(c)·f(b)﹤0,则c就是函数的零点。则令b=c(此时零点 x 0 ∈(a,c));
则令a=c(此时零点 x 0 ∈(c,b);
应用:利用计算器求方程2 x+3x=7的近似解(精确度0.1)。解:原方程即为2 x+3x-7=0,令f(x)= 2 x+3x-7。因为︱1.375-1.4375 ︱ =0.0625<0.1
所以原方程的近似解可取1.4375f(x)= 2 x+3x-7-1 0 1 2通过计算得下表可知f(1)·f(2)<0,说明在区间(1,2)内有零点。作出函数的对应值表与图象↑y↑xy练习:2。某方程有一无理根在 区间D=(0,3)内,若用二分
法求此根的近似值,将区间D至少等分 ___ 次后,
所得近似值可精确到0.1。51.下列函数图象均与x轴有交点其中不能用二分法求图中
函数零点的图号是( )AC作业:
借助计算器,用二分法求方程x=3-lgx在
区间(2,3)内的近似解(精确度0.1) 。
1.什么是二分法;
2.用二分法求方程近似解的步骤。课堂小结谢谢合作!再见
已知假银元比真银元稍轻点儿。现在只有一个天平,
如何找出假银元?思考,探究, 发现一元二次方程可以用公式求根,
如何求方程lnx+2x-6=0的根呢?找函数
f(x)=lnx+2x-6
的零点.f(x)=lnx+2x-6-10 -5 5 10 ↓↓↓yx0转化方程f(x)=0有根等价于______________函数y=f(x)有零点求方程的根就是______________
找对应函数的零点函数y=f(x)的图象在区间[a,b]上是一条
___________的曲线,且___________,则函数在区间(a,b)上有零点。 f(a)?f(b)<0时连续不断 2.50000 -0.0831 2.50000 3.000002.5 根 2.5625找函数f(x)=lnx+2x-6的零点近似值(精确度为0.1)2.75因为︱2.5-2.5625︱=0.0625 <0.1时,2.5(或2.5625)就是方程lnx+2x-6=0的近似解2.75000 0.51160二分法定义:
对于在区间[a,b]上连续不断且f(a)·f(b)<0的函数
y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,
使区间的两个端点逐步逼近零点,进而得到零点近似值的方
法叫做二分法 .______________归纳:用二分法求函数f(x)零点近似值的步骤: 1.确定区间[a,b],验证f(a )·f(b)﹤0,给定精确度m;2.求区间(a,b)的中点c;3.计算f(c);4.判断是否达到精确度;若︱ a-b︱﹤m则得到零点
近似值a(或b);否则重复2~4。(1)若f(c)=0,(2)若f(a)·f(c)﹤0,(3)若f(c)·f(b)﹤0,则c就是函数的零点。则令b=c(此时零点 x 0 ∈(a,c));
则令a=c(此时零点 x 0 ∈(c,b);
应用:利用计算器求方程2 x+3x=7的近似解(精确度0.1)。解:原方程即为2 x+3x-7=0,令f(x)= 2 x+3x-7。因为︱1.375-1.4375 ︱ =0.0625<0.1
所以原方程的近似解可取1.4375f(x)= 2 x+3x-7-1 0 1 2通过计算得下表可知f(1)·f(2)<0,说明在区间(1,2)内有零点。作出函数的对应值表与图象↑y↑xy练习:2。某方程有一无理根在 区间D=(0,3)内,若用二分
法求此根的近似值,将区间D至少等分 ___ 次后,
所得近似值可精确到0.1。51.下列函数图象均与x轴有交点其中不能用二分法求图中
函数零点的图号是( )AC作业:
借助计算器,用二分法求方程x=3-lgx在
区间(2,3)内的近似解(精确度0.1) 。
1.什么是二分法;
2.用二分法求方程近似解的步骤。课堂小结谢谢合作!再见
