北师大版七年级数学上册2.7有理数乘法课件
文档属性
| 名称 | 北师大版七年级数学上册2.7有理数乘法课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 189.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-17 00:00:00 | ||
图片预览




文档简介
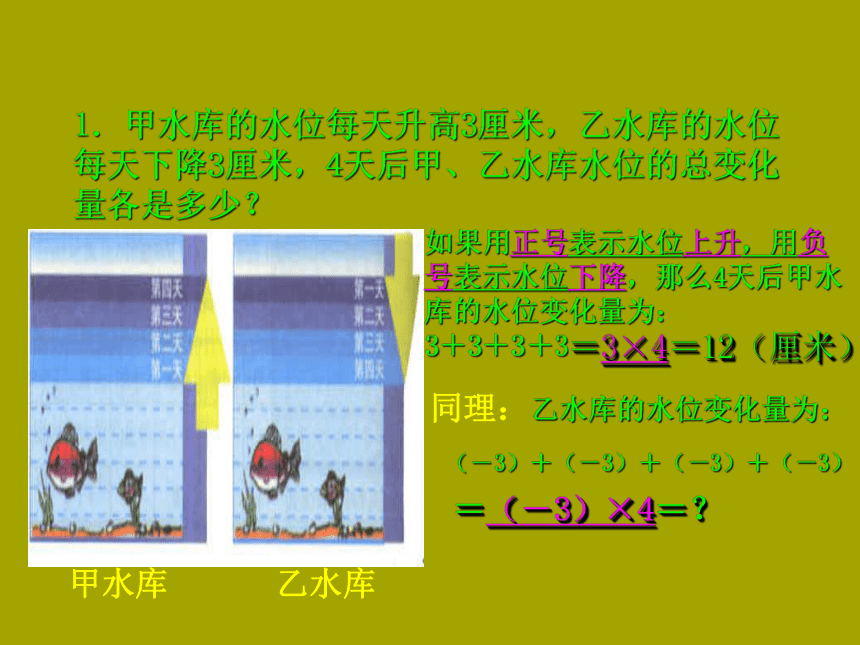
课件20张PPT。2.8 有理数的乘法第二章、有理数及其运算1.甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后甲、乙水库水位的总变化量各是多少?如果用正号表示水位上升,用负号表示水位下降,那么4天后甲水库的水位变化量为:
3+3+3+3同理:乙水库的水位变化量为:(-3)+(-3)+(-3)+(-3)甲水库乙水库=3×4=12(厘米)=(-3)×4=?有理数乘法的类型:1、正数×正数
2、负数×负数
3、正数×负数
4、负数×正数
5、0 ×正数
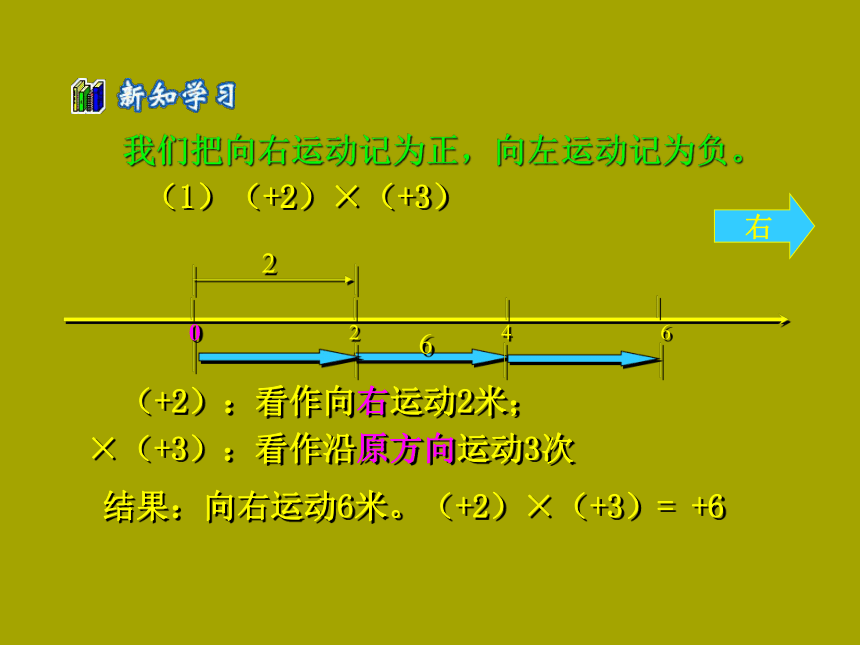
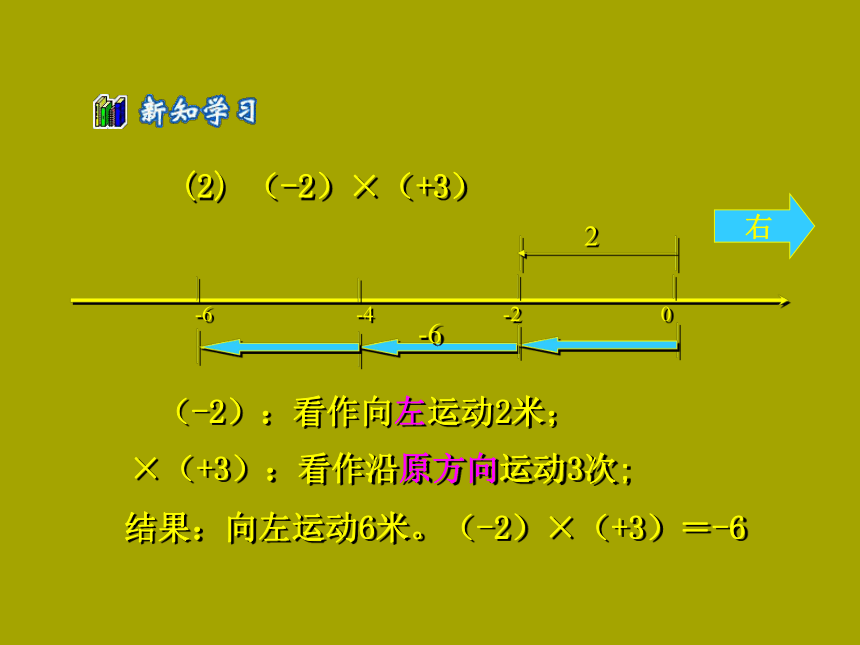
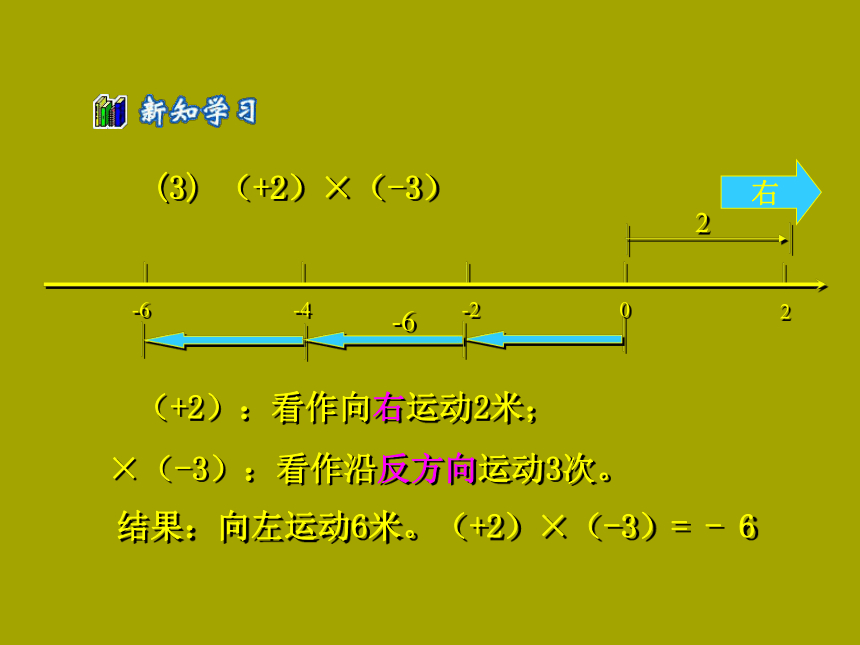
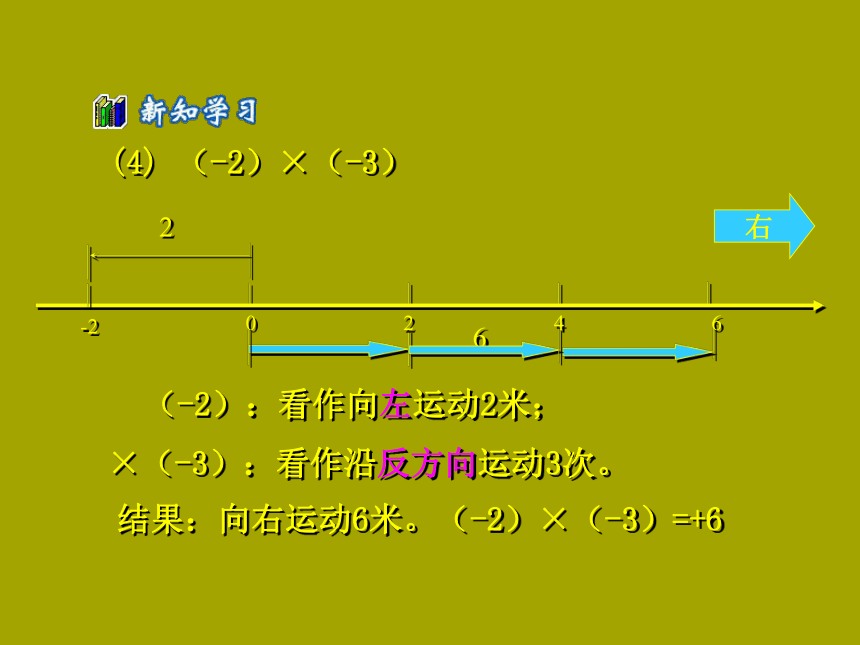
6、0 ×负数(1)(+2)×(+3)(+2):看作向右运动2米;×(+3):看作沿原方向运动3次结果:向右运动6米。(+2)×(+3)= +6我们把向右运动记为正,向左运动记为负。(2) (-2)×(+3)(-2):看作向左运动2米;×(+3):看作沿原方向运动3次;结果:向左运动6米。(-2)×(+3)=-6(3) (+2)×(-3)(+2):看作向右运动2米;×(-3):看作沿反方向运动3次。结果:向左运动6米。(+2)×(-3)= - 6(4) (-2)×(-3)(-2):看作向左运动2米;×(-3):看作沿反方向运动3次。结果:向右运动6米。(-2)×(-3)=+6(5) 0 × 5 = 0在原地运动5次(-5)× 0 = 0向左方运动0次结果:被乘数是0或者乘数是0,结果仍为0。 0 × 0 = 0(1)2×3=6
(2)(-2)×(-3)=6
(3)(-2)×3= -6
(4)2×(-3)= -6
(5) 被乘数或乘数为0时,结果是0 有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。5个例子综合如下:同号相乘 积为正数异号相乘 积为负数练习1:先确定下列积的号,然后试计算结果:
(1) 5×(-3)
(2)(-4)×6
(3)(-7)×(-9)
(4) 0.5×0.7积的符号为负
积的符号为负
积的符号为正
积的符号为正进行两个有理数的运算时,
先确定积的符号,再把绝对值相乘,=-15
=-24
=63
=0.35例1: (-7) ×(- 4)(同号两数乘)解:(-7)×(- 4)
=(同号得正)= + 28(把绝对值相乘)例2:(-4)×5 ×(-0.25)(从左向右依次运算)解:原式= 〔(-4)×5〕×(-0.25)异号得负
绝对值相乘同号得正
绝对值相乘=+(20×0.25)( 7×4 )+=〔-(4×5)〕×(-0.25) =(-20)×(-0.25) = 5观察(3)、(4)两题你有什么发现?能得出什么结论?
观察(5)、(6)两题你有什么发现?能得出什么结论?注意:
a、一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
b、乘积为1的两个有理数互为倒数练习2:确定下列积的号并计算:(1)(-3)×8×2.5 (2)(-3)×(-8)×2.5
(3)(-3)×(-8)×(2.5)
(4)(-3)× 0× (-8)×(2.5)
(议一议)几个有理数相乘,因数都不为0时,积的符号怎样确定? 有一个因数为0时,积是多少?几个有理数相乘,积的符号由负因数的个数确定:
负因数的个数为偶数个,则积为正数
负因数的个数为奇数个,则积为负数
当有一个因数为零时,积为零。计算(口答):
(1) 6×(-9)=
(2)(-6)×(-9)=
(3)(-6)×9 =(4) (-6)×1=
(5) ( -6)×(-1) =
(6) 6×(-1) =填空:
1×(-5)=___ (-1)×(-5)=___
(2)1× a =___ (-1)× a =___-55a-a-5454-54-66-6用“<”或“>”号填空:(1)如果a<0 b>0那么 ab___0
(2)如果a<0 b<0那么 ab___0=-1.5=-4=0><判断下列方程的解是正数、负数还是0:
(1) 4X= -16 (2)-3X=18
(3)-9X=-36 (4)-5X=0思考题
(1)当a>0时,a与2a哪个大?
(2)当a<0时,a与2a那个大?正数负数0负数2a大a大小结:1.有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个有理数的运算:先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。注意:
a、一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
c、乘积为1的两个有理数互为倒数作业:
P76 : 知识技能 1.计算
再见
3+3+3+3同理:乙水库的水位变化量为:(-3)+(-3)+(-3)+(-3)甲水库乙水库=3×4=12(厘米)=(-3)×4=?有理数乘法的类型:1、正数×正数
2、负数×负数
3、正数×负数
4、负数×正数
5、0 ×正数
6、0 ×负数(1)(+2)×(+3)(+2):看作向右运动2米;×(+3):看作沿原方向运动3次结果:向右运动6米。(+2)×(+3)= +6我们把向右运动记为正,向左运动记为负。(2) (-2)×(+3)(-2):看作向左运动2米;×(+3):看作沿原方向运动3次;结果:向左运动6米。(-2)×(+3)=-6(3) (+2)×(-3)(+2):看作向右运动2米;×(-3):看作沿反方向运动3次。结果:向左运动6米。(+2)×(-3)= - 6(4) (-2)×(-3)(-2):看作向左运动2米;×(-3):看作沿反方向运动3次。结果:向右运动6米。(-2)×(-3)=+6(5) 0 × 5 = 0在原地运动5次(-5)× 0 = 0向左方运动0次结果:被乘数是0或者乘数是0,结果仍为0。 0 × 0 = 0(1)2×3=6
(2)(-2)×(-3)=6
(3)(-2)×3= -6
(4)2×(-3)= -6
(5) 被乘数或乘数为0时,结果是0 有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。5个例子综合如下:同号相乘 积为正数异号相乘 积为负数练习1:先确定下列积的号,然后试计算结果:
(1) 5×(-3)
(2)(-4)×6
(3)(-7)×(-9)
(4) 0.5×0.7积的符号为负
积的符号为负
积的符号为正
积的符号为正进行两个有理数的运算时,
先确定积的符号,再把绝对值相乘,=-15
=-24
=63
=0.35例1: (-7) ×(- 4)(同号两数乘)解:(-7)×(- 4)
=(同号得正)= + 28(把绝对值相乘)例2:(-4)×5 ×(-0.25)(从左向右依次运算)解:原式= 〔(-4)×5〕×(-0.25)异号得负
绝对值相乘同号得正
绝对值相乘=+(20×0.25)( 7×4 )+=〔-(4×5)〕×(-0.25) =(-20)×(-0.25) = 5观察(3)、(4)两题你有什么发现?能得出什么结论?
观察(5)、(6)两题你有什么发现?能得出什么结论?注意:
a、一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
b、乘积为1的两个有理数互为倒数练习2:确定下列积的号并计算:(1)(-3)×8×2.5 (2)(-3)×(-8)×2.5
(3)(-3)×(-8)×(2.5)
(4)(-3)× 0× (-8)×(2.5)
(议一议)几个有理数相乘,因数都不为0时,积的符号怎样确定? 有一个因数为0时,积是多少?几个有理数相乘,积的符号由负因数的个数确定:
负因数的个数为偶数个,则积为正数
负因数的个数为奇数个,则积为负数
当有一个因数为零时,积为零。计算(口答):
(1) 6×(-9)=
(2)(-6)×(-9)=
(3)(-6)×9 =(4) (-6)×1=
(5) ( -6)×(-1) =
(6) 6×(-1) =填空:
1×(-5)=___ (-1)×(-5)=___
(2)1× a =___ (-1)× a =___-55a-a-5454-54-66-6用“<”或“>”号填空:(1)如果a<0 b>0那么 ab___0
(2)如果a<0 b<0那么 ab___0=-1.5=-4=0><判断下列方程的解是正数、负数还是0:
(1) 4X= -16 (2)-3X=18
(3)-9X=-36 (4)-5X=0思考题
(1)当a>0时,a与2a哪个大?
(2)当a<0时,a与2a那个大?正数负数0负数2a大a大小结:1.有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个有理数的运算:先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。注意:
a、一个数同+1相乘,得原数,一个数同-1相乘,得原数的相反数。
c、乘积为1的两个有理数互为倒数作业:
P76 : 知识技能 1.计算
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
