相似三角形判定2

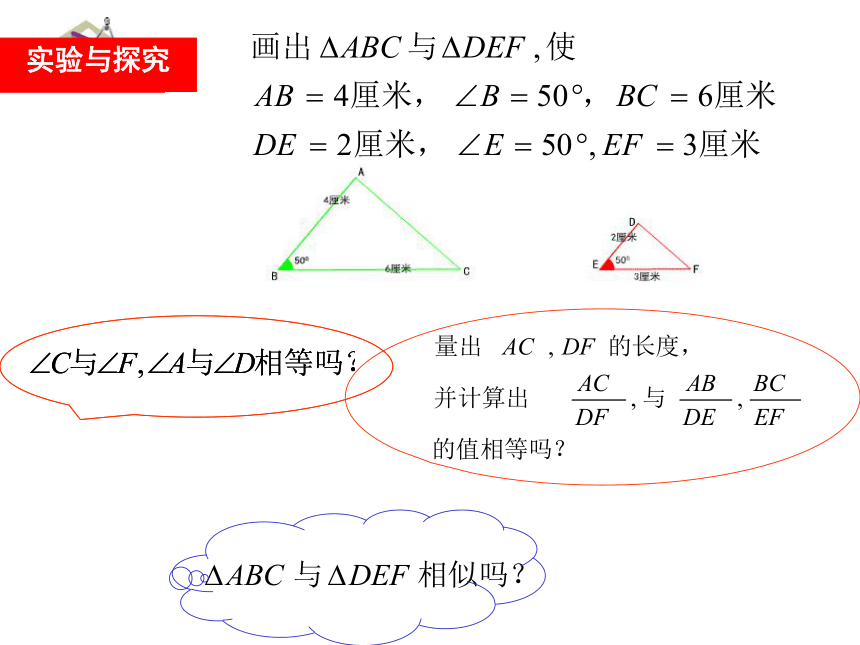
课件13张PPT。怎样判定三角形相似（2）学习目标：掌握“如果一个三角形两条边与另一个三角形两条边对应成比例，并且夹角相等，那么这两个三角形相似”这一判定方法,并运用判定方法解决问题。 1:
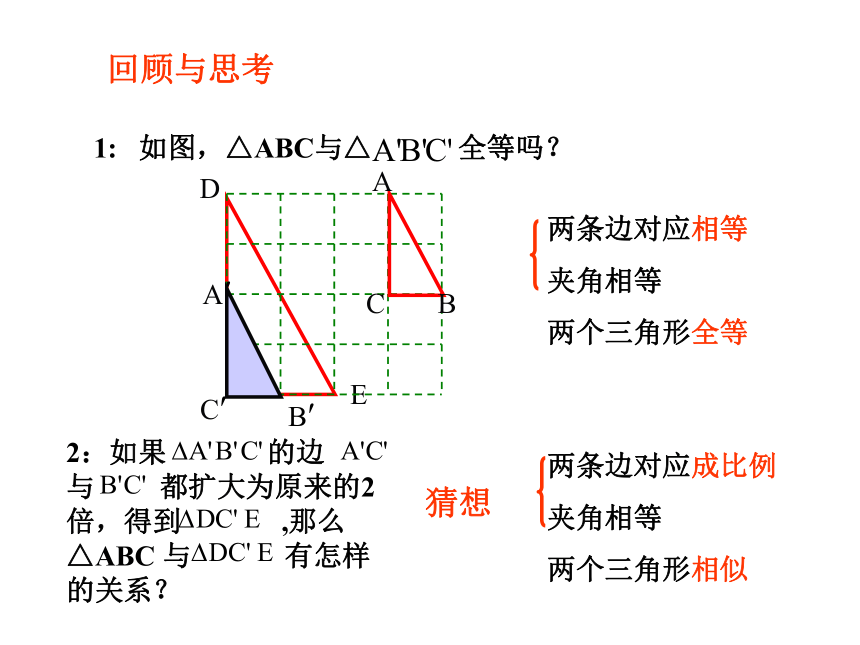
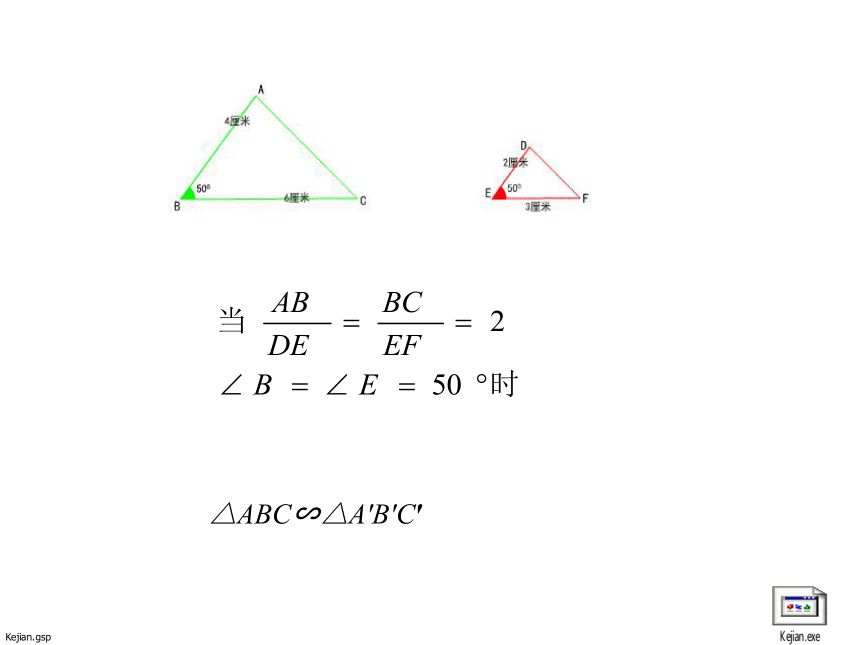
2:经历判定两个三角形相似条件的探索过程，积累数学活动的经验。体会类比的学习方法.B′猜想回顾与思考2：如果 的边 与 都扩大为原来的2倍，得到 ,那么△ABC 与 有怎样的关系？△ABC∽△A′B′C′
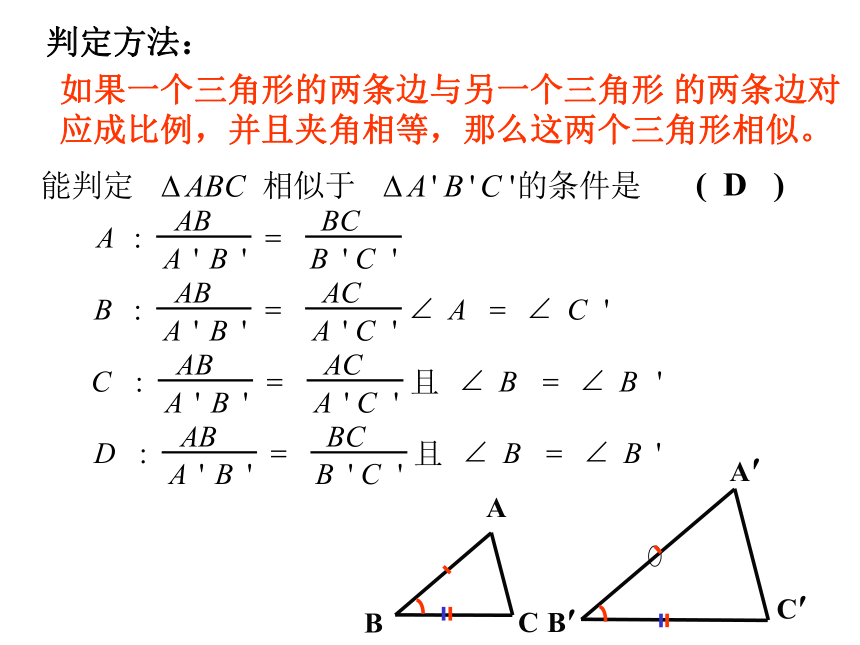
( )D如果一个三角形的两条边与另一个三角形 的两条边对应成比例，并且夹角相等，那么这两个三角形相似。判定方法：例题：如图AD=3,AE=4,BE=5, CD=9.
△ADE和△ABC相 似吗？所以△ADE∽△ABCABCDE3459解：这个方案是可行的。

因为 且
∠ECD=∠BCA,
所以△ECD∽△BCA,
因此：AB????CA1:为了测量池塘边上A,B两点的距离，小亮设计了一个方案：先在平地上取一点可以到达A和B的点C,然后在射线AC和BC上分别
取一 点D和E,使 ,量出DE的长度，那么AB
的长度就可以计算出来.你认为他的方案可行吗？为什么？2、如图，在△ABC中，点D在AB上，请再添加一个 适当的条件，使△ADC∽△ACB，那么可添加的条件是（ ） 2︰3.请同学们先阅读课本43页小莹的方案，然后思考她的方案为什么正确？你能设计一个方案吗？通过这节课的学习你有什么收获?1：必做题：课本第49页
A组 第5、7两题2：选做题：第55页 第8题再见谢谢同学们的合作！1：在△ABC和△DEF中，如果∠B和∠E同时增加或减少相同的度数，而
保持AB,DE,BC,EF的长度不变， △ABC和△DEF还相似吗？