沪科版八年级下册第19章《19.3 矩形 菱形 正方形》教学设计
文档属性
| 名称 | 沪科版八年级下册第19章《19.3 矩形 菱形 正方形》教学设计 | 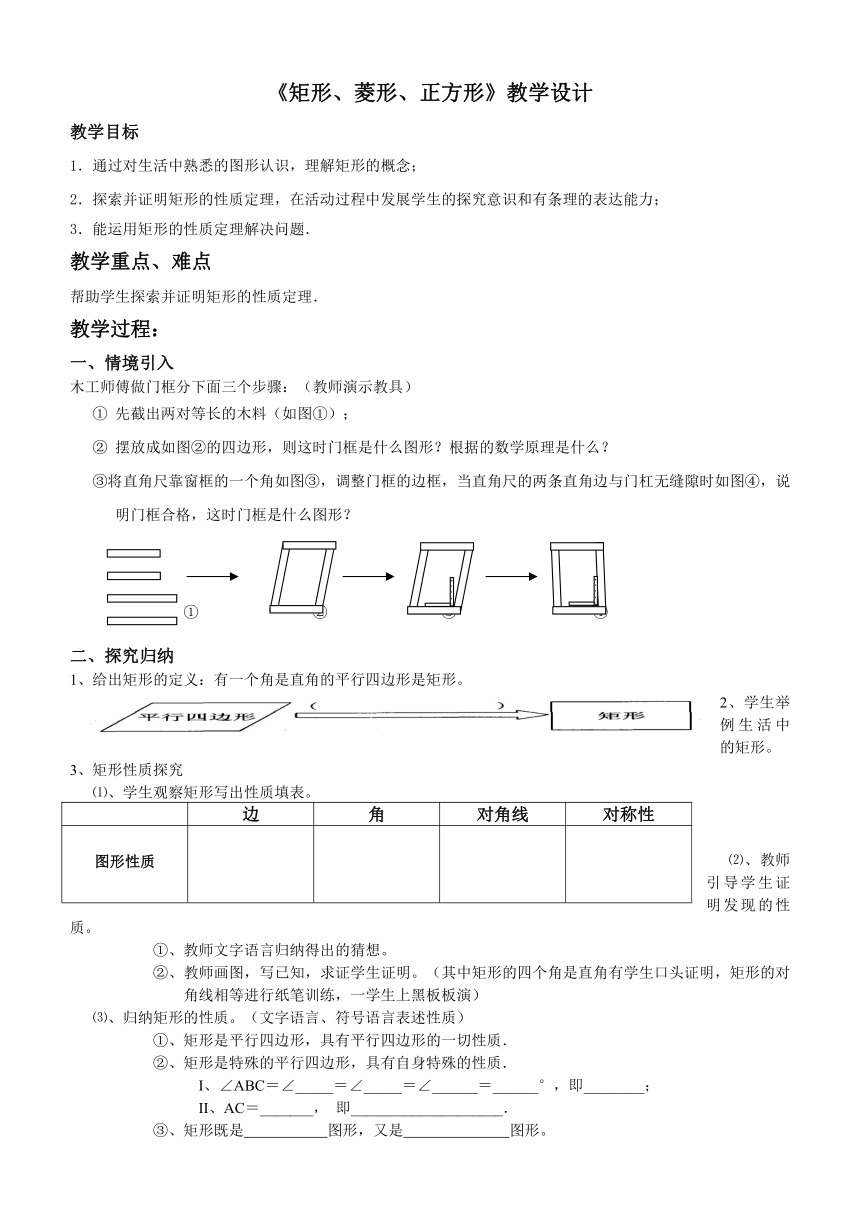 | |
| 格式 | zip | ||
| 文件大小 | 69.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-18 11:22:26 | ||
图片预览


文档简介
《矩形、菱形、正方形》教学设计
教学目标
1.通过对生活中熟悉的图形认识,理解矩形的概念;
2.探索并证明矩形的性质定理,在活动过程中发展学生的探究意识和有条理的表达能力;
3.能运用矩形的性质定理解决问题.
教学重点、难点
帮助学生探索并证明矩形的性质定理.
教学过程:
一、情境引入
木工师傅做门框分下面三个步骤:(教师演示教具)
①
先截出两对等长的木料(如图①);
②
摆放成如图②的四边形,则这时门框是什么图形?根据的数学原理是什么?
③将直角尺靠窗框的一个角如图③,调整门框的边框,当直角尺的两条直角边与门杠无缝隙时如图④,说明门框合格,这时门框是什么图形?
①
②
③
④
二、探究归纳
1、给出矩形的定义:有一个角是直角的平行四边形是矩形。
2、学生举例生活中的矩形。
3、矩形性质探究
⑴、学生观察矩形写出性质填表。
边
角
对角线
对称性
图形性质
⑵、教师引导学生证明发现的性质。
①、教师文字语言归纳得出的猜想。
②、教师画图,写已知,求证学生证明。(其中矩形的四个角是直角有学生口头证明,矩形的对角线相等进行纸笔训练,一学生上黑板板演)
⑶、归纳矩形的性质。(文字语言、符号语言表述性质)
①、矩形是平行四边形,具有平行四边形的一切性质.
②、矩形是特殊的平行四边形,具有自身特殊的性质.
I、∠ABC=∠_____=∠_____=∠______=______°,即________;
II、AC=_______,
即____________________.
③、矩形既是
图形,又是
图形。
⑷、结合图形填空
①、矩形ABCD中,AB=6,BC=8,则AC=
,BD=
。
②、矩形ABCD中,
AO=7,AC=
,
BD=
,
B0=
。
你还可以求出哪些边的长度?
③、矩形ABCD中,∠BOC=100°,∠OAD=
,∠OBA=
。
4、例题教学
1、 已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.
⑴、求证:△AOB是等边三角形.
⑵、在矩形ABCD中,要使△AOB是等边三角形,
你还可以加其它什么条件?
⑶、在矩形ABCD中,要使△AOB是等腰直角三角形,你可以增加什么条件?
(学生先独立思考后,写出证明过程,然后小组交流补充,形成完整的有条理的证明过程.)
证明:∵四边形ABCD是矩形,
∴AC=BD,AO=CO=AC,BO=DO=BD,
∵AC=2AB,
∴AO=BO=AB.
∴△AOB是等边三角形
三、巩固练习
1、如图,矩形ABCD的对角线AC,BD相交于点O,BD=10,∠BOC=120°,
求矩形的面积。
2、如图在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.
性质
对边平行
对边相等
对角线互相平分
对角相等
4个角都是直角
是轴对称图形
是中心对称图形
任意平行四边形
矩形
四、小结本课
辨析:下表中的图形如果具有该条性质,在表格中打
“√”
五、布置作业
《数学补充习题》P31
《矩形、菱形、正方形1》
六、补充习题
1、如图,将矩形ABCD沿对角线BD折叠,使点C与点C'重合,若AB=2,则C’D的长为
(
)
A.1
B.2
C.3
D.4
2、如图,在矩形ABCD中,E为BC的中点,作∠AEC的平分线交AD于点F.若AB=6,AD=16,则FD的长度为
(
)
A.4
B.5
C.6
D.8
3、若矩形的一条对角线长为10,则另一条对角线长为_______;若还知道它的一边长为8,则该矩形的面积为_______.
5、在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.
求证:DF=DC.
6、如图,在矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,试说明BE=CF.
8、如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边上的点F处,折痕为AE,求CE的长.
9、如图,在矩形ABCD中,AE平分∠DAB交DC于点E,连接BE,过点E作EF⊥BE交AD于点F.
(1)求证:∠DEF=∠CBE;
(2)请找出图中与BE相等的线段(不另添加辅助线和字母),并说明
理由.
提示:根据条件,我们可以知道∠DEF与∠CBE都是∠CEB的余角,
则它们是等角,并可以得到△CBF≌△DEF,则有EF=BE.
10、如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、AC的长分别为3和5,那么点P到矩形的两条对角线AC和BD的距离之和是(
)
A.
B.
C.
D.不确定
七、课后反思
本节课教师引导学生与平行四边形的学习类比,从边、角、对角线、对称性等方面研究矩形,教师帮助学生归纳出矩形具有的平行四边形的一般性质和矩形所具有的特殊性质。而后教师通过例题的教学帮助学生更好的掌握矩形的性质,并了解矩形性质的常见应用:①矩形中的4个等腰三角形及特例等边三角形的边角计算,②矩形中找直角三角形用勾股定理计算边、对角线。
学法上:学生经历观察猜想矩形性质——证明矩形性质——归纳矩形性质定理——应用矩形性质定理解决问题的过程。
不足之处:①整节课的教学显得有点松,以至于课堂上学生没有足够的时间练习,对矩形的性质定理巩固不够。
②对学生出现的一些问题(如学生写的全等式字母不对应)没有及时指出错误。
③对例题1变式教学归纳的不好,没做好相等边、不等边的分类。
教学目标
1.通过对生活中熟悉的图形认识,理解矩形的概念;
2.探索并证明矩形的性质定理,在活动过程中发展学生的探究意识和有条理的表达能力;
3.能运用矩形的性质定理解决问题.
教学重点、难点
帮助学生探索并证明矩形的性质定理.
教学过程:
一、情境引入
木工师傅做门框分下面三个步骤:(教师演示教具)
①
先截出两对等长的木料(如图①);
②
摆放成如图②的四边形,则这时门框是什么图形?根据的数学原理是什么?
③将直角尺靠窗框的一个角如图③,调整门框的边框,当直角尺的两条直角边与门杠无缝隙时如图④,说明门框合格,这时门框是什么图形?
①
②
③
④
二、探究归纳
1、给出矩形的定义:有一个角是直角的平行四边形是矩形。
2、学生举例生活中的矩形。
3、矩形性质探究
⑴、学生观察矩形写出性质填表。
边
角
对角线
对称性
图形性质
⑵、教师引导学生证明发现的性质。
①、教师文字语言归纳得出的猜想。
②、教师画图,写已知,求证学生证明。(其中矩形的四个角是直角有学生口头证明,矩形的对角线相等进行纸笔训练,一学生上黑板板演)
⑶、归纳矩形的性质。(文字语言、符号语言表述性质)
①、矩形是平行四边形,具有平行四边形的一切性质.
②、矩形是特殊的平行四边形,具有自身特殊的性质.
I、∠ABC=∠_____=∠_____=∠______=______°,即________;
II、AC=_______,
即____________________.
③、矩形既是
图形,又是
图形。
⑷、结合图形填空
①、矩形ABCD中,AB=6,BC=8,则AC=
,BD=
。
②、矩形ABCD中,
AO=7,AC=
,
BD=
,
B0=
。
你还可以求出哪些边的长度?
③、矩形ABCD中,∠BOC=100°,∠OAD=
,∠OBA=
。
4、例题教学
1、 已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.
⑴、求证:△AOB是等边三角形.
⑵、在矩形ABCD中,要使△AOB是等边三角形,
你还可以加其它什么条件?
⑶、在矩形ABCD中,要使△AOB是等腰直角三角形,你可以增加什么条件?
(学生先独立思考后,写出证明过程,然后小组交流补充,形成完整的有条理的证明过程.)
证明:∵四边形ABCD是矩形,
∴AC=BD,AO=CO=AC,BO=DO=BD,
∵AC=2AB,
∴AO=BO=AB.
∴△AOB是等边三角形
三、巩固练习
1、如图,矩形ABCD的对角线AC,BD相交于点O,BD=10,∠BOC=120°,
求矩形的面积。
2、如图在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.
性质
对边平行
对边相等
对角线互相平分
对角相等
4个角都是直角
是轴对称图形
是中心对称图形
任意平行四边形
矩形
四、小结本课
辨析:下表中的图形如果具有该条性质,在表格中打
“√”
五、布置作业
《数学补充习题》P31
《矩形、菱形、正方形1》
六、补充习题
1、如图,将矩形ABCD沿对角线BD折叠,使点C与点C'重合,若AB=2,则C’D的长为
(
)
A.1
B.2
C.3
D.4
2、如图,在矩形ABCD中,E为BC的中点,作∠AEC的平分线交AD于点F.若AB=6,AD=16,则FD的长度为
(
)
A.4
B.5
C.6
D.8
3、若矩形的一条对角线长为10,则另一条对角线长为_______;若还知道它的一边长为8,则该矩形的面积为_______.
5、在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.
求证:DF=DC.
6、如图,在矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,试说明BE=CF.
8、如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边上的点F处,折痕为AE,求CE的长.
9、如图,在矩形ABCD中,AE平分∠DAB交DC于点E,连接BE,过点E作EF⊥BE交AD于点F.
(1)求证:∠DEF=∠CBE;
(2)请找出图中与BE相等的线段(不另添加辅助线和字母),并说明
理由.
提示:根据条件,我们可以知道∠DEF与∠CBE都是∠CEB的余角,
则它们是等角,并可以得到△CBF≌△DEF,则有EF=BE.
10、如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、AC的长分别为3和5,那么点P到矩形的两条对角线AC和BD的距离之和是(
)
A.
B.
C.
D.不确定
七、课后反思
本节课教师引导学生与平行四边形的学习类比,从边、角、对角线、对称性等方面研究矩形,教师帮助学生归纳出矩形具有的平行四边形的一般性质和矩形所具有的特殊性质。而后教师通过例题的教学帮助学生更好的掌握矩形的性质,并了解矩形性质的常见应用:①矩形中的4个等腰三角形及特例等边三角形的边角计算,②矩形中找直角三角形用勾股定理计算边、对角线。
学法上:学生经历观察猜想矩形性质——证明矩形性质——归纳矩形性质定理——应用矩形性质定理解决问题的过程。
不足之处:①整节课的教学显得有点松,以至于课堂上学生没有足够的时间练习,对矩形的性质定理巩固不够。
②对学生出现的一些问题(如学生写的全等式字母不对应)没有及时指出错误。
③对例题1变式教学归纳的不好,没做好相等边、不等边的分类。
