2.1.2.2.指数函数性质的应用 同步训练(含答案)
文档属性
| 名称 | 2.1.2.2.指数函数性质的应用 同步训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 70.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-19 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
2.1.2.2.指数函数性质的应用 同步训练(含答案)
1.下列判断正确的是( )
A.2.52.5>2.52.6 B.0.82<0.83 C.< D.0.90.3>0.90.4
2.若函数f(x)=2x+2-x与g(x)=2x-2-x的定义域为R,则( )
A.f(x)与g(x)均为偶函数 B.f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数 D.f(x)为奇函数,g(x)为偶函数
3.已知f(x)=a-x(a>0,且a≠1),且f(2)>f(-3),则a的取值范围是( )
A.a>0 B.a>1 C.a<1 D.04.定义运算ab:ab= ,如2=1,则函数f(x)=的值域为 ( )
A.(0,+∞) B.R C.(0,1] D.[1,+∞)
5.函数y=的单调递增区间为( )
A.(-∞,+∞) B.(0,+∞) C.(1,+∞) D.(0,1)
6.若<,则实数a的取值范围是( )
A.(1,+∞) B.(,+) C.(-∞,1) D.(-,)
7.当x∈(-∞, -1]时,不等式(m2-m)6x-3x<0恒成立,则实数m的取值范围是( )
A.(-2,1) B.(-4,3) C.(-1, 2) D.(-3, 4)
8.若函数f(x)=是R上的增函数,则实数a的取值范围为( )
A.(1,8 ) B.(1,+∞) C.(4,8) D.[4,8)
二、填空题
9.若函数f(x)=的定义域为R,则实数m的取值范围是________.
10.若方程++m=0有正数解,则实数m的取值范围是_______.
11.已知函数f(x)=,则f(x)的单调递增区间是________.
12.用清水漂洗衣服,假如每次能够洗除去污垢的,要使存留污垢不超过原来的1%,则至少要漂洗________次.21·cn·jy·com
13.已知定义在(-,+)上的偶函数f(x)在区间[0,+∞)上是单调减函数,若f(1)>f(lg),则x的取值范围为 .【来源:21·世纪·教育·网】
三、解答题
14.已知函数f(x)=.
(1)若a=-1时,求函数f(x)的单调增区间;
(2)如果函数f(x)有最大值3,求实数a的值.
15.已知函数f(x)=a-(x∈R).
(1)用定义证明:不论a为何实数,f(x)在R上为增函数;
(2)若f(x)为奇函数,求a的值;
(3)在(2)的条件下,求f(x)在区间[1,5]上的最小值.
参考答案:
1.解析:∵y=0.9x是减函数,且0.4>0.3,∴0.90.3>0.90.4.答案:D
2.解析:f(-x)=2-x+2x=f(x),f(x)为偶函数,g(-x)=2-x-2x=-g(x),g(x)为奇函数.答案:B21·世纪*教育网
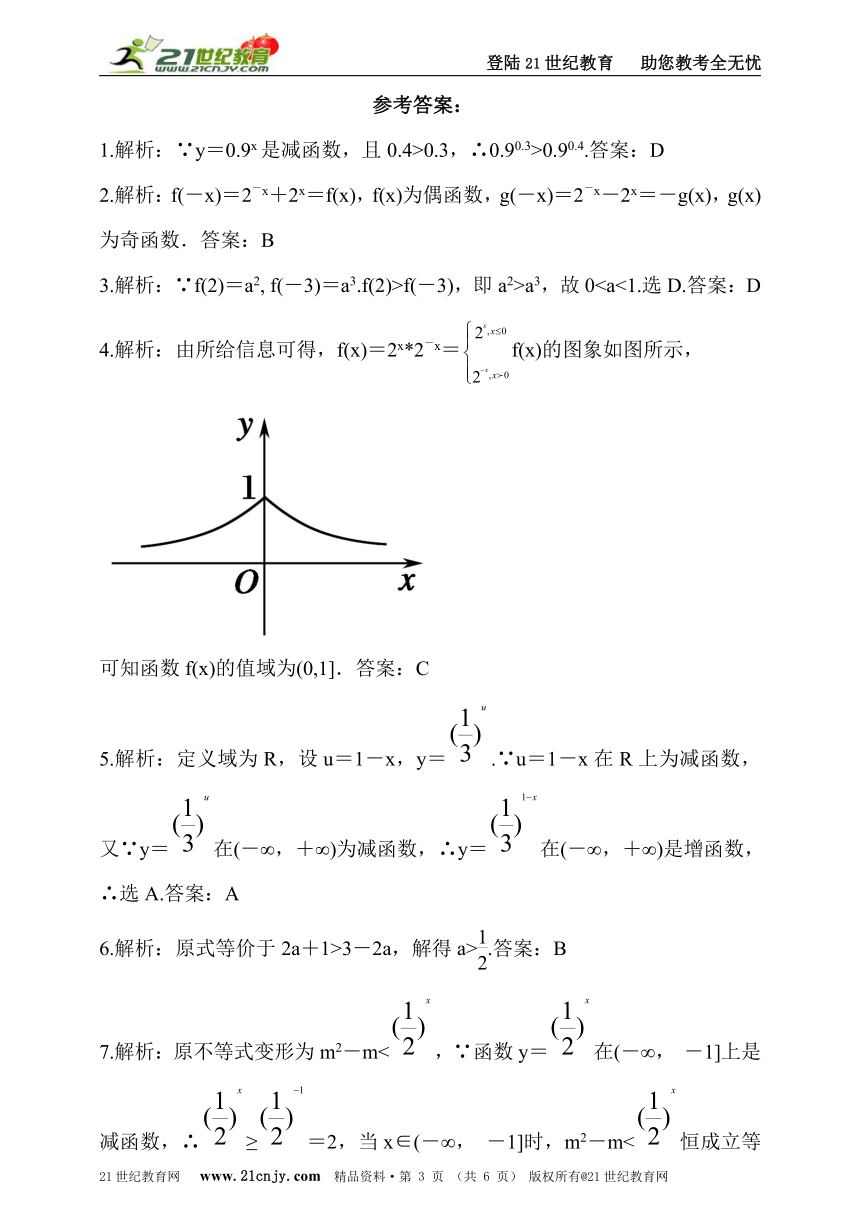
3.解析:∵f(2)=a2, f(-3)=a3.f(2)>f(-3),即a2>a3,故04.解析:由所给信息可得,f(x)=2x*2-x=f(x)的图象如图所示,
可知函数f(x)的值域为(0,1].答案:C
5.解析:定义域为R,设u=1-x,y=.∵u=1-x在R上为减函数,又∵y=在(-∞,+∞)为减函数,∴y=在(-∞,+∞)是增函数,
∴选A.答案:A
6.解析:原式等价于2a+1>3-2a,解得a>.答案:B
7.解析:原不等式变形为m2-m<,∵函数y=在(-∞, -1]上是减函数,∴≥=2,当x∈(-∞, -1]时,m2-m<恒成立等价于m2-m<2,解得-18.解析:由题可知,f(x)在R上是增函数,所以解得4≤a<8,故选D.答案:D
9.解析:依题意,≥0对x∈R恒成立,即x2+2mx-m≥0恒成立,
∴Δ=4m2+4m≤0,-1≤m≤0.答案:[-1,0]
10.解析:令=t,∵方程有正根,∴t∈(0,1).方程转化为t2+2t+m=0.∴m=1-(t+1)2,∵t∈(0,1),∴m∈(-3,0).答案:(-3,0)
11.解析:由指数函数的性质可知f(x)=x在定义域上为减函数,故要求f(x)的单调递增区间,只需求y=|x-1|的单调递减区间.又y=|x-1|的单调递减区间为(-∞,1],所以f(x)的单调递增区间为(-∞,1].
答案:(-∞,1]
12.解析:设原来污垢数为1个单位,则经过第一次漂洗,存留量为原来的;经过第二次漂洗,存留量为第一次漂洗后的,也就是原来的,经过第三次漂洗,存留量为原来的,……,经过第x次漂洗,存留量为原来的,故解析式为y=.由题意,≤,4x≥100,2x≥10,∴x≥4,即至少漂洗4次.答案:421教育网
13.解析:因为f(x)是定义在R上的偶函数且在区间[0,+∞)上是单调减函数,
所以f(x)在区间(-∞,0)上是增函数,所以不等式f(1)>f(lg)可化为lg>1或lg<-1,所以lg>lg10或lg10或0<<,所以010.
答案:010
解:(1)当a=-1时,f(x)=,令g(x)=-x2-4x+3=-(x+2)2+7,由于g(x)在(-2,+∞)上递减,y=在R上是减函数,∴f(x)在
(-2,+∞)上是增函数,即f(x)的单调增区间是(-2,+∞).
(2)令h(x)=ax2-4x+3,f(x)=,由于f(x)有最大值3,所以h(x)应有最小值-1;因此必有解得a=1.即当f(x)有最大值3时,a的值为1.21cnjy.com
15.解:(1)证明:f(x)的定义域为R,设x1,x2是R上的任意两个不相等的实数,且x1(2)∵f(x)为奇函数,∴f(0)=0,即a-=0,解得a=.
(3)由(2)知,f(x)=-.由(1)知,f(x)在(-∞,+∞)上为增函数,∴f(x)在区间[1,5]上的最小值为f(1).∵f(1)=-=,∴f(x)在区间[1,5]上的最小值为.2·1·c·n·j·y
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
2.1.2.2.指数函数性质的应用 同步训练(含答案)
1.下列判断正确的是( )
A.2.52.5>2.52.6 B.0.82<0.83 C.< D.0.90.3>0.90.4
2.若函数f(x)=2x+2-x与g(x)=2x-2-x的定义域为R,则( )
A.f(x)与g(x)均为偶函数 B.f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数 D.f(x)为奇函数,g(x)为偶函数
3.已知f(x)=a-x(a>0,且a≠1),且f(2)>f(-3),则a的取值范围是( )
A.a>0 B.a>1 C.a<1 D.0
A.(0,+∞) B.R C.(0,1] D.[1,+∞)
5.函数y=的单调递增区间为( )
A.(-∞,+∞) B.(0,+∞) C.(1,+∞) D.(0,1)
6.若<,则实数a的取值范围是( )
A.(1,+∞) B.(,+) C.(-∞,1) D.(-,)
7.当x∈(-∞, -1]时,不等式(m2-m)6x-3x<0恒成立,则实数m的取值范围是( )
A.(-2,1) B.(-4,3) C.(-1, 2) D.(-3, 4)
8.若函数f(x)=是R上的增函数,则实数a的取值范围为( )
A.(1,8 ) B.(1,+∞) C.(4,8) D.[4,8)
二、填空题
9.若函数f(x)=的定义域为R,则实数m的取值范围是________.
10.若方程++m=0有正数解,则实数m的取值范围是_______.
11.已知函数f(x)=,则f(x)的单调递增区间是________.
12.用清水漂洗衣服,假如每次能够洗除去污垢的,要使存留污垢不超过原来的1%,则至少要漂洗________次.21·cn·jy·com
13.已知定义在(-,+)上的偶函数f(x)在区间[0,+∞)上是单调减函数,若f(1)>f(lg),则x的取值范围为 .【来源:21·世纪·教育·网】
三、解答题
14.已知函数f(x)=.
(1)若a=-1时,求函数f(x)的单调增区间;
(2)如果函数f(x)有最大值3,求实数a的值.
15.已知函数f(x)=a-(x∈R).
(1)用定义证明:不论a为何实数,f(x)在R上为增函数;
(2)若f(x)为奇函数,求a的值;
(3)在(2)的条件下,求f(x)在区间[1,5]上的最小值.
参考答案:
1.解析:∵y=0.9x是减函数,且0.4>0.3,∴0.90.3>0.90.4.答案:D
2.解析:f(-x)=2-x+2x=f(x),f(x)为偶函数,g(-x)=2-x-2x=-g(x),g(x)为奇函数.答案:B21·世纪*教育网
3.解析:∵f(2)=a2, f(-3)=a3.f(2)>f(-3),即a2>a3,故0
可知函数f(x)的值域为(0,1].答案:C
5.解析:定义域为R,设u=1-x,y=.∵u=1-x在R上为减函数,又∵y=在(-∞,+∞)为减函数,∴y=在(-∞,+∞)是增函数,
∴选A.答案:A
6.解析:原式等价于2a+1>3-2a,解得a>.答案:B
7.解析:原不等式变形为m2-m<,∵函数y=在(-∞, -1]上是减函数,∴≥=2,当x∈(-∞, -1]时,m2-m<恒成立等价于m2-m<2,解得-1
9.解析:依题意,≥0对x∈R恒成立,即x2+2mx-m≥0恒成立,
∴Δ=4m2+4m≤0,-1≤m≤0.答案:[-1,0]
10.解析:令=t,∵方程有正根,∴t∈(0,1).方程转化为t2+2t+m=0.∴m=1-(t+1)2,∵t∈(0,1),∴m∈(-3,0).答案:(-3,0)
11.解析:由指数函数的性质可知f(x)=x在定义域上为减函数,故要求f(x)的单调递增区间,只需求y=|x-1|的单调递减区间.又y=|x-1|的单调递减区间为(-∞,1],所以f(x)的单调递增区间为(-∞,1].
答案:(-∞,1]
12.解析:设原来污垢数为1个单位,则经过第一次漂洗,存留量为原来的;经过第二次漂洗,存留量为第一次漂洗后的,也就是原来的,经过第三次漂洗,存留量为原来的,……,经过第x次漂洗,存留量为原来的,故解析式为y=.由题意,≤,4x≥100,2x≥10,∴x≥4,即至少漂洗4次.答案:421教育网
13.解析:因为f(x)是定义在R上的偶函数且在区间[0,+∞)上是单调减函数,
所以f(x)在区间(-∞,0)上是增函数,所以不等式f(1)>f(lg)可化为lg>1或lg<-1,所以lg>lg10或lg
答案:0
解:(1)当a=-1时,f(x)=,令g(x)=-x2-4x+3=-(x+2)2+7,由于g(x)在(-2,+∞)上递减,y=在R上是减函数,∴f(x)在
(-2,+∞)上是增函数,即f(x)的单调增区间是(-2,+∞).
(2)令h(x)=ax2-4x+3,f(x)=,由于f(x)有最大值3,所以h(x)应有最小值-1;因此必有解得a=1.即当f(x)有最大值3时,a的值为1.21cnjy.com
15.解:(1)证明:f(x)的定义域为R,设x1,x2是R上的任意两个不相等的实数,且x1
(3)由(2)知,f(x)=-.由(1)知,f(x)在(-∞,+∞)上为增函数,∴f(x)在区间[1,5]上的最小值为f(1).∵f(1)=-=,∴f(x)在区间[1,5]上的最小值为.2·1·c·n·j·y
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 1 页) 版权所有@21世纪教育网
