人教A版必修一第一章《1.2.1 函数的概念》课件 (共23张PPT)
文档属性
| 名称 | 人教A版必修一第一章《1.2.1 函数的概念》课件 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 874.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-19 13:14:20 | ||
图片预览







文档简介
课件23张PPT。§1.2.1 函数的概念
数学天才——莱布尼兹
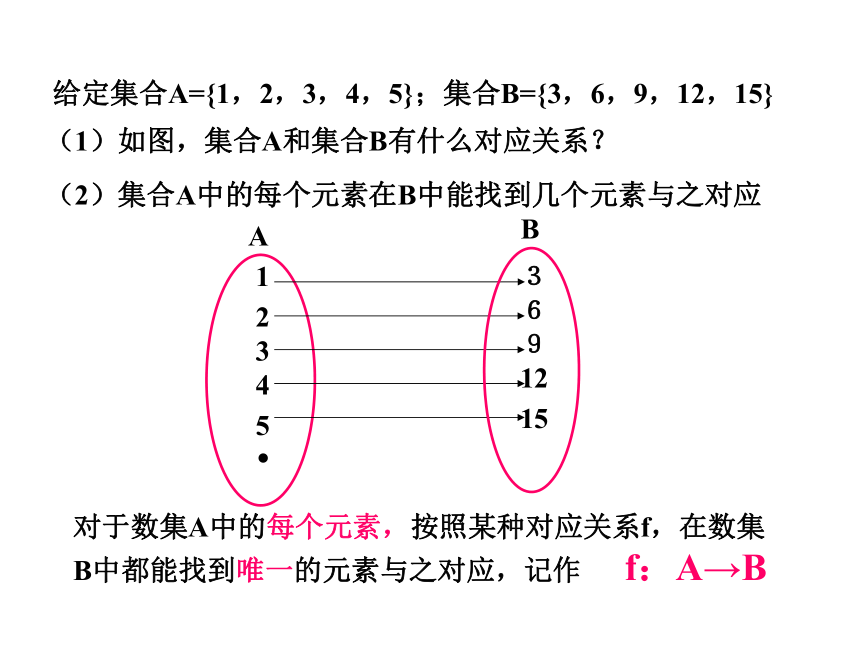
函数这个数学名词是莱布尼兹在1694年开始使用的,以描述曲线的一个相关量,如曲线的斜率或者曲线上的某一点。莱布尼兹所指的函数现在被称作可导函数,数学家之外的普通人一般接触到的函数即属此类。对于可导函数可以讨论它的极限和导数。此两者描述了函数输出值的变化同输入值变化的关系,是微积分学的基础。 一、复习引入:初中(传统)的函数的定义是什么?初中学过哪些函数? 设在一个变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数. 这种用变量叙述的函数定义我们称之为函数的传统定义.初中已经学过:正比例函数、反比例函数、一次函数、二次函数等。 对于数集A中的每个元素,按照某种对应关系f,在数集B中都能找到唯一的元素与之对应,记作 f:A→B 问题一:给定集合A={1,2,3,4,5};集合B={3,6,9,12,15}×3(1)如图,集合A和集合B有什么对应关系?(2)集合A中的每个元素在B中能找到几个元素与之对应函数:
设集合A,B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,集合B中都有唯一确定的数 f(x)和它对应,那么称 f:A→B 为从集合A到集合B的一个函数,记作
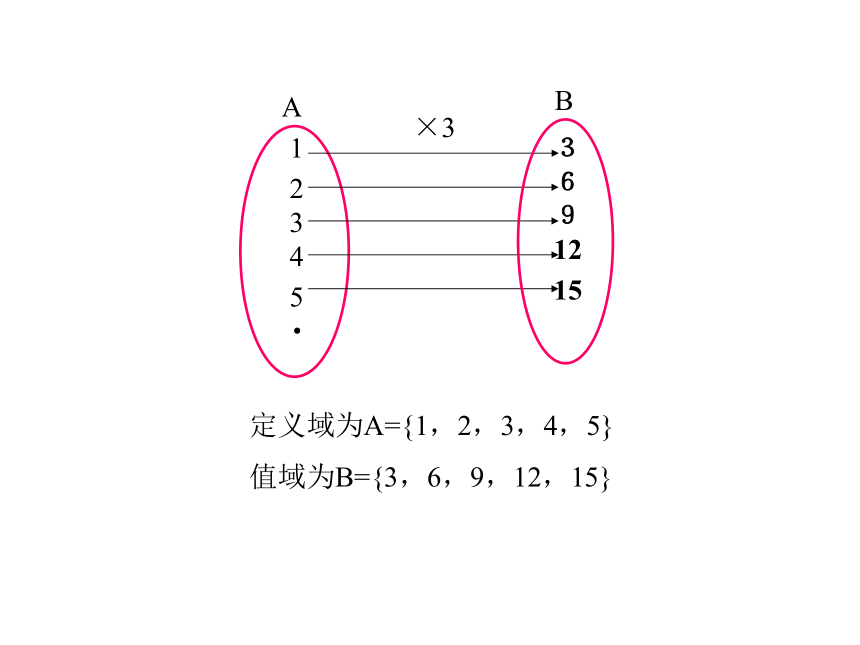
y = f(x) , x∈A.则 y=3x , x∈A
即 f(x)=3x , x∈A(1)定义域 :x叫做自变量。(2)值域:与x值相对应的值y叫做函数值。
x的取值范围A叫做函数的定义域; 函数值的集合{f(x) ︳x∈A}叫做函数的值域。
定义域为A={1,2,3,4,5}
值域为B={3,6,9,12,15}
例如:
(1)一次函数y=ax+b(a≠0)定义域为R值域为R(2)二次函数 练习:求下列函数的定义域:(1)(2)分析:答案:答案:分析:归纳:确定用解析式表示的函数的定义域的一般方法:1、f(x)是整式2、f(x)是分式3、f(x)是二次根式4、如果f(x)由几个部分
的数学式子构成的?函数的定义域是R;?函数的定义域是使
分母不为0的实数
的集合;?函数的定义域是
使被开方式不小
于0的实数的集合;?定义域是使各
部分都有意义的
实数集合。 例题分析解(1) 有意义的实数x的集合是{x|x≥-3}
有意义的实数x的集合是{x|x≠-2} 所以
这个函数的定义域就是
(2)(3)因为a>0,所以f(a),f(a-1)有意义函数定义域值域对应关系 *值域是由定义域和对应关系决定的。 *如果两个函数的定义域和对应关系完 全一致,就知这两个函数相等。函数有三要素,即: 例2下列函数哪个与函数y=x相等 解(1) ,这个函数与y=x(x∈R)
对应一样,定义域不不同,所以和y=x (x∈R)不相等 (2) 这个函数和y=x (x∈R)
对应关系一样 ,定义域相同x∈R,所以和y=x (x∈R)相等(4) 的定义域是{x|x≠0},与函数 y=x(x∈R)
的对应关系一样,但是定义域 不同,所以和y=x(x∈R)不相
等 例2下列函数哪个与函数y=x相等3.下列各组函数中,是否表示同一函数?设a,b是两个实数,而且a(1)、满足不等式a≤x≤b的实数x的集合叫做闭区间,表示为 [a,b].
(2)、满足不等式a(3)、满足不等式a≤xa,x≤a,x{x|5 ≤ x<6} (2) {x|x ≥9}
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
(4) {x|x < 9}∪{x| -9 < x<20}例3 设f(x)的定义域是[-1,3],试求函数f(2x+1)的定义域。 分析:函数f(2x+1)的自变是仍是x,不是2x+1,故应由2x+1满足的条件中求出x的取值范围,进而得所求定义域。
解:由已知-1≤2x+1≤3,得-1≤x≤1。得函数f(2x+1)的定义域是[-1,1] 。拓展例4(1)(孪生问题1)已知f(x)=x2-x+1,求f(2x+1)。 (2) (孪生问题2)已知f(2x+1)的定义域是[-1,3],且f(x)的定义域由f(2x+1)确定,试求f(x)的定义域。解(1):f(2x+1)=(2x+1)2-(2x+1)+1=4x2+2x+1。
解(2):由已知-1≤x≤3,得2x+1∈[-1,7],又f(x)的定义域由f(2x+1)确定,故f(x)的定义域为[-1,7]。
注:(1)f(x)意含对x的一种运算法则;
(2)解题时经常将一个变量作为整体看;
(3) 2x+1∈[-1,7]与-1≤2x+1≤7是同义句。拓展作业:
P24 A组 1 ,4
设集合A,B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,集合B中都有唯一确定的数 f(x)和它对应,那么称 f:A→B 为从集合A到集合B的一个函数,记作
y = f(x) , x∈A.则 y=3x , x∈A
即 f(x)=3x , x∈A(1)定义域 :x叫做自变量。(2)值域:与x值相对应的值y叫做函数值。
x的取值范围A叫做函数的定义域; 函数值的集合{f(x) ︳x∈A}叫做函数的值域。
定义域为A={1,2,3,4,5}
值域为B={3,6,9,12,15}
例如:
(1)一次函数y=ax+b(a≠0)定义域为R值域为R(2)二次函数 练习:求下列函数的定义域:(1)(2)分析:答案:答案:分析:归纳:确定用解析式表示的函数的定义域的一般方法:1、f(x)是整式2、f(x)是分式3、f(x)是二次根式4、如果f(x)由几个部分
的数学式子构成的?函数的定义域是R;?函数的定义域是使
分母不为0的实数
的集合;?函数的定义域是
使被开方式不小
于0的实数的集合;?定义域是使各
部分都有意义的
实数集合。 例题分析解(1) 有意义的实数x的集合是{x|x≥-3}
有意义的实数x的集合是{x|x≠-2} 所以
这个函数的定义域就是
(2)(3)因为a>0,所以f(a),f(a-1)有意义函数定义域值域对应关系 *值域是由定义域和对应关系决定的。 *如果两个函数的定义域和对应关系完 全一致,就知这两个函数相等。函数有三要素,即: 例2下列函数哪个与函数y=x相等 解(1) ,这个函数与y=x(x∈R)
对应一样,定义域不不同,所以和y=x (x∈R)不相等 (2) 这个函数和y=x (x∈R)
对应关系一样 ,定义域相同x∈R,所以和y=x (x∈R)相等(4) 的定义域是{x|x≠0},与函数 y=x(x∈R)
的对应关系一样,但是定义域 不同,所以和y=x(x∈R)不相
等 例2下列函数哪个与函数y=x相等3.下列各组函数中,是否表示同一函数?设a,b是两个实数,而且a
(2)、满足不等式a
(3) {x|x ≤ -1} ∩{x| -5 ≤ x<2}
(4) {x|x < 9}∪{x| -9 < x<20}例3 设f(x)的定义域是[-1,3],试求函数f(2x+1)的定义域。 分析:函数f(2x+1)的自变是仍是x,不是2x+1,故应由2x+1满足的条件中求出x的取值范围,进而得所求定义域。
解:由已知-1≤2x+1≤3,得-1≤x≤1。得函数f(2x+1)的定义域是[-1,1] 。拓展例4(1)(孪生问题1)已知f(x)=x2-x+1,求f(2x+1)。 (2) (孪生问题2)已知f(2x+1)的定义域是[-1,3],且f(x)的定义域由f(2x+1)确定,试求f(x)的定义域。解(1):f(2x+1)=(2x+1)2-(2x+1)+1=4x2+2x+1。
解(2):由已知-1≤x≤3,得2x+1∈[-1,7],又f(x)的定义域由f(2x+1)确定,故f(x)的定义域为[-1,7]。
注:(1)f(x)意含对x的一种运算法则;
(2)解题时经常将一个变量作为整体看;
(3) 2x+1∈[-1,7]与-1≤2x+1≤7是同义句。拓展作业:
P24 A组 1 ,4
