人教A版高中数学必修5《1.1.2余弦定理》优秀课件 (共22张PPT)
文档属性
| 名称 | 人教A版高中数学必修5《1.1.2余弦定理》优秀课件 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-19 13:15:30 | ||
图片预览








文档简介
课件22张PPT。余 弦 定 理用正弦定理解三角形需要已知哪些条件? ①两角和一边,②两边和其中一边的对角。正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
[复习回顾] 思考:如果在一个斜三角形中,已知两边及这两边的夹角,能否用正弦定理解这个三角形,为什么? 不能,在正弦定理 中,已知两边及这两边的夹角,正弦定理的任一等号两边都有两个未知量。那么,怎么解这个三角形呢?同理,从 出发, 证得
从 出发,证得 证明: 学过向量之后,我们能用向量的方法给予证明余弦定理。已知AB,AC和它们的夹角A,求CB即[向量法][解析法](bcosC,bsinC)(a,0)(0,0)证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:同理:(bcosC,bsinC)(a,0)(0,0)[解析法]当角C为锐角时几何法
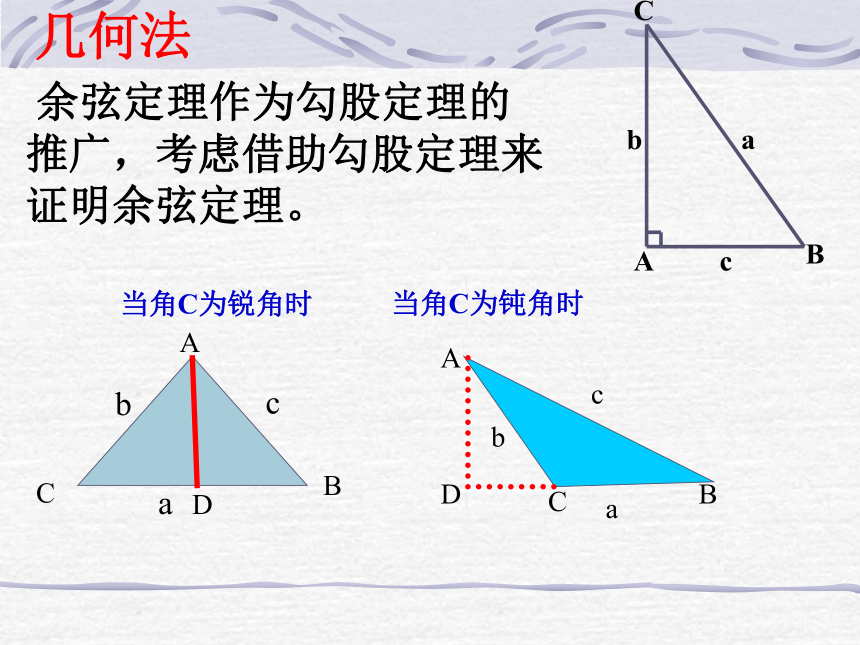
当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。在锐角三角形ABC中,已知AB=c,AC=b和A,求a同理有: 同样,对于钝角三角形及直角三角形,上面三个等式成立的,课后请同学们自己证明。[几何法]用语言描述:三角形任何一边的平方等于其它两边的平方和, 再减去这两边与它们夹角的余弦的积的两倍。余 弦 定 理例1:若已知b=8,c=3,A= ,能求a吗?思考:余弦定理还有别的用途吗?若已知a,b,c,可以求什么?解:余弦定理的变形:例2、在三角形ABC中,已知a=7,b=10,c=6,求A,B,C(精确到 )分析:已知三边,求三个角,可用余弦定理的变形来解决问题解:练一练: 1、已知△ABC的三边为 、2、1,求它的最大内角。变一变:若已知三边的比是 :2:1,又怎么求? 归纳:
利用余弦定理可以解决以下两类有关三角形的问题: (1)已知三边,求三个角 (2)已知两边和它们的夹角,求第三边,进而还可求其它两个角。解:由余弦定理得:例3、在△ABC中,若a=4、b=5、c=6
(1)试判断角C是什么角?
(2)判断△ABC的形状变式训练:在△ABC中,若 ,则△ABC的形状
为( )A、钝角三角形 B、直角三角形
C、锐角三角形 D、不能确定A提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形推论:判断三角形的形状练习:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足B练习:在三角形ABC中,已知a=7,b=8,cosC= ,求最大角的余弦值分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。解:则有:b是最大边,那么B 是最大角(1)余弦定理适用于任何三角形(3)由余弦定理可知:(2)余弦定理的作用: a、已知三边,求三个角 b、已知两边及这两边的夹角,求第三边,进而可求出其它两个角c、判断三角形的形状[小结] 正余弦定理在解三角形中能解决哪些问题?角边角
角角边
边边角
边角边
边边边正弦定理余弦定理运用 例2、在三角形ABC中,已知a=2.730,b=3.696,C= ,
解这个三角形(边长保留四个有效数字,角度精确到 )分析:已知两边和两边的夹角解:[数学运用]思考: (1)还可怎样求角A? (2)角A会有两解吗?
[复习回顾] 思考:如果在一个斜三角形中,已知两边及这两边的夹角,能否用正弦定理解这个三角形,为什么? 不能,在正弦定理 中,已知两边及这两边的夹角,正弦定理的任一等号两边都有两个未知量。那么,怎么解这个三角形呢?同理,从 出发, 证得
从 出发,证得 证明: 学过向量之后,我们能用向量的方法给予证明余弦定理。已知AB,AC和它们的夹角A,求CB即[向量法][解析法](bcosC,bsinC)(a,0)(0,0)证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:同理:(bcosC,bsinC)(a,0)(0,0)[解析法]当角C为锐角时几何法
当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。在锐角三角形ABC中,已知AB=c,AC=b和A,求a同理有: 同样,对于钝角三角形及直角三角形,上面三个等式成立的,课后请同学们自己证明。[几何法]用语言描述:三角形任何一边的平方等于其它两边的平方和, 再减去这两边与它们夹角的余弦的积的两倍。余 弦 定 理例1:若已知b=8,c=3,A= ,能求a吗?思考:余弦定理还有别的用途吗?若已知a,b,c,可以求什么?解:余弦定理的变形:例2、在三角形ABC中,已知a=7,b=10,c=6,求A,B,C(精确到 )分析:已知三边,求三个角,可用余弦定理的变形来解决问题解:练一练: 1、已知△ABC的三边为 、2、1,求它的最大内角。变一变:若已知三边的比是 :2:1,又怎么求? 归纳:
利用余弦定理可以解决以下两类有关三角形的问题: (1)已知三边,求三个角 (2)已知两边和它们的夹角,求第三边,进而还可求其它两个角。解:由余弦定理得:例3、在△ABC中,若a=4、b=5、c=6
(1)试判断角C是什么角?
(2)判断△ABC的形状变式训练:在△ABC中,若 ,则△ABC的形状
为( )A、钝角三角形 B、直角三角形
C、锐角三角形 D、不能确定A提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形推论:判断三角形的形状练习:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足B练习:在三角形ABC中,已知a=7,b=8,cosC= ,求最大角的余弦值分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。解:则有:b是最大边,那么B 是最大角(1)余弦定理适用于任何三角形(3)由余弦定理可知:(2)余弦定理的作用: a、已知三边,求三个角 b、已知两边及这两边的夹角,求第三边,进而可求出其它两个角c、判断三角形的形状[小结] 正余弦定理在解三角形中能解决哪些问题?角边角
角角边
边边角
边角边
边边边正弦定理余弦定理运用 例2、在三角形ABC中,已知a=2.730,b=3.696,C= ,
解这个三角形(边长保留四个有效数字,角度精确到 )分析:已知两边和两边的夹角解:[数学运用]思考: (1)还可怎样求角A? (2)角A会有两解吗?
