人教A版高中数学必修一:3.1.1《方程的根与函数的零点》 课件 (共19张PPT)
文档属性
| 名称 | 人教A版高中数学必修一:3.1.1《方程的根与函数的零点》 课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 602.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-19 13:16:23 | ||
图片预览






文档简介
课件19张PPT。方程的根与函数的零点带岭区高级中学 荆藜藜2018/11/11学习目标:
1、理解函数零点的概念
2、领会函数零点与相应方程间的关系
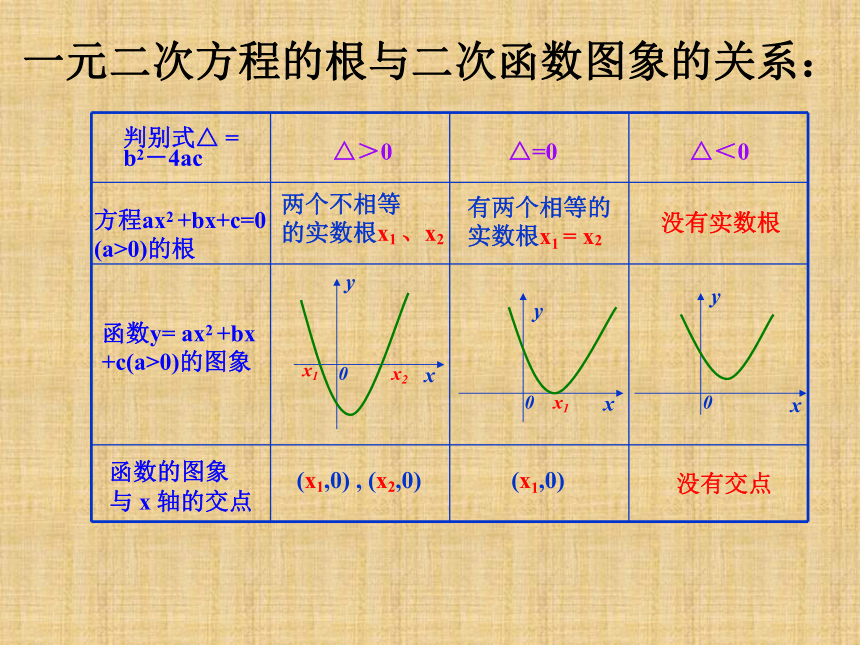
3、掌握零点存在性定理及判定条件2018/11/11方程ax2 +bx+c=0
(a>0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2一元二次方程的根与二次函数图象的关系: 对于函数y=f(x),我们把使f(x)=0的实数x叫
做函数y=f(x)的零点。方程f(x)=0有实数根函数零点的定义:等价关系数x112018/11/11①(代数法)求方程的实数根;
②(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点.函数零点的求法:2018/11/11指出下列函数的零点:1、函数y=x2-2x-32、函数y=x2-2x+13、函数y=2x-1x=3和x=-1x=1x=0抢答:如果把函数比作一部电影,那么函数的零点就像是电影的一个瞬间,一个镜头。有时我们会忽略一些镜头,但是我们仍然能推测出被忽略的片断。现在我有两组镜头(如图),哪一组能说明他的行程一定曾渡过河??????????????
(Ⅰ)
(Ⅱ)
探索:函数零点的存在性 2018/11/11将河流抽象成x轴,将前后的两个位置视为A、B两点。请问当A、B与x轴怎样的位置关系时,AB间的一段连续不断的函数图象一定会与x轴有交点?A、B两点在x轴的两侧时2018/11/11A、B位于x轴两侧,如何用数学符号(式子)来表示?答:A、B两点在x轴的两侧
可以用f(a)·f(b)<0来表示。提示:A点位置用函数值f(a)表示
B点位置用函数值f(b)表示 零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。结论: 在区间[a,b] 上的图象是连续不断的一条曲线f(a)·f(b)<0仅有一个至少有一个52018/11/11在区间 [2,4]上,f(2)___0 ,f(4)___0,f(2)·f(4)___0
在区间(2,4)上,x=3 是 x2-2x-3=0的另一个根
则x=3也为函数的零点><<<<>在区间[-2,1]上,f(-2) __0, f(1)___0,
则 f(-2)· f(1) ___0 ,
在区间(-2,1)上,x=-1是 x2 -2x-3=0的一个根
则x=-1为函数的零点零点存在性定理的应用:2018/11/11由表和图可知:f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内有零点。由于函数f(x)在定义域(0,+∞)内是
增函数,所以它仅有一个零点.
这个零点所在的大致区间是(2,3)解:用计算器或计算机作出x、f(x)的对应值表和图象-4 -1.30691.09863.38635.60947.79189.945912.079414.1972例题 求函数f(x)=lnx+2x-6的零点个数及零点所在的大致区间。2018/11/11求函数f(x)=lnx+2x-6的零点个数及零点所在的大致区间。知识扩充:
用另外一种解法(不允许使用计算器):2018/11/11方程 lnx=6-2x 的近似解1、对于定义在R上的函数y=f(x),若f(a).f(b)<0 (a,b R,且aA 只有一个零点 B 至少有一个零点
C 无零点 D 无法确定有无零点当堂检测:2、如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是( )
A m> – 2 B m< – 2 C m>2 D m<2
3、函数f(x)=x3-16x的零点为( )
A (0,0),(4,0) B 0,4 C (– 4 ,0), (0,0),(4,0) D – 4 ,0,4
4、方程lnx= 必有一个根的区间是( )
A (1,2) B (2,3) C ( , 1 ) D (3,+ )BBDB5、已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:那么函数在区间[1,6]上的零点至少有( )个
A 5 B 4 C 3 D 2
C小结与思考函数零点的定义等价关系函数的零点存在性定理
及存在的零点个数的判断2018/11/11谢谢!
1、理解函数零点的概念
2、领会函数零点与相应方程间的关系
3、掌握零点存在性定理及判定条件2018/11/11方程ax2 +bx+c=0
(a>0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2一元二次方程的根与二次函数图象的关系: 对于函数y=f(x),我们把使f(x)=0的实数x叫
做函数y=f(x)的零点。方程f(x)=0有实数根函数零点的定义:等价关系数x112018/11/11①(代数法)求方程的实数根;
②(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点.函数零点的求法:2018/11/11指出下列函数的零点:1、函数y=x2-2x-32、函数y=x2-2x+13、函数y=2x-1x=3和x=-1x=1x=0抢答:如果把函数比作一部电影,那么函数的零点就像是电影的一个瞬间,一个镜头。有时我们会忽略一些镜头,但是我们仍然能推测出被忽略的片断。现在我有两组镜头(如图),哪一组能说明他的行程一定曾渡过河??????????????
(Ⅰ)
(Ⅱ)
探索:函数零点的存在性 2018/11/11将河流抽象成x轴,将前后的两个位置视为A、B两点。请问当A、B与x轴怎样的位置关系时,AB间的一段连续不断的函数图象一定会与x轴有交点?A、B两点在x轴的两侧时2018/11/11A、B位于x轴两侧,如何用数学符号(式子)来表示?答:A、B两点在x轴的两侧
可以用f(a)·f(b)<0来表示。提示:A点位置用函数值f(a)表示
B点位置用函数值f(b)表示 零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。结论: 在区间[a,b] 上的图象是连续不断的一条曲线f(a)·f(b)<0仅有一个至少有一个52018/11/11在区间 [2,4]上,f(2)___0 ,f(4)___0,f(2)·f(4)___0
在区间(2,4)上,x=3 是 x2-2x-3=0的另一个根
则x=3也为函数的零点><<<<>在区间[-2,1]上,f(-2) __0, f(1)___0,
则 f(-2)· f(1) ___0 ,
在区间(-2,1)上,x=-1是 x2 -2x-3=0的一个根
则x=-1为函数的零点零点存在性定理的应用:2018/11/11由表和图可知:f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内有零点。由于函数f(x)在定义域(0,+∞)内是
增函数,所以它仅有一个零点.
这个零点所在的大致区间是(2,3)解:用计算器或计算机作出x、f(x)的对应值表和图象-4 -1.30691.09863.38635.60947.79189.945912.079414.1972例题 求函数f(x)=lnx+2x-6的零点个数及零点所在的大致区间。2018/11/11求函数f(x)=lnx+2x-6的零点个数及零点所在的大致区间。知识扩充:
用另外一种解法(不允许使用计算器):2018/11/11方程 lnx=6-2x 的近似解1、对于定义在R上的函数y=f(x),若f(a).f(b)<0 (a,b R,且a
C 无零点 D 无法确定有无零点当堂检测:2、如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是( )
A m> – 2 B m< – 2 C m>2 D m<2
3、函数f(x)=x3-16x的零点为( )
A (0,0),(4,0) B 0,4 C (– 4 ,0), (0,0),(4,0) D – 4 ,0,4
4、方程lnx= 必有一个根的区间是( )
A (1,2) B (2,3) C ( , 1 ) D (3,+ )BBDB5、已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:那么函数在区间[1,6]上的零点至少有( )个
A 5 B 4 C 3 D 2
C小结与思考函数零点的定义等价关系函数的零点存在性定理
及存在的零点个数的判断2018/11/11谢谢!
