人教A版数学必修二2.3.1 直线与平面所成的角 课件 (共22张PPT)
文档属性
| 名称 | 人教A版数学必修二2.3.1 直线与平面所成的角 课件 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-19 13:16:55 | ||
图片预览




文档简介
课件22张PPT。直线和平面
所成的角Bqr6401@126.com直线和平面
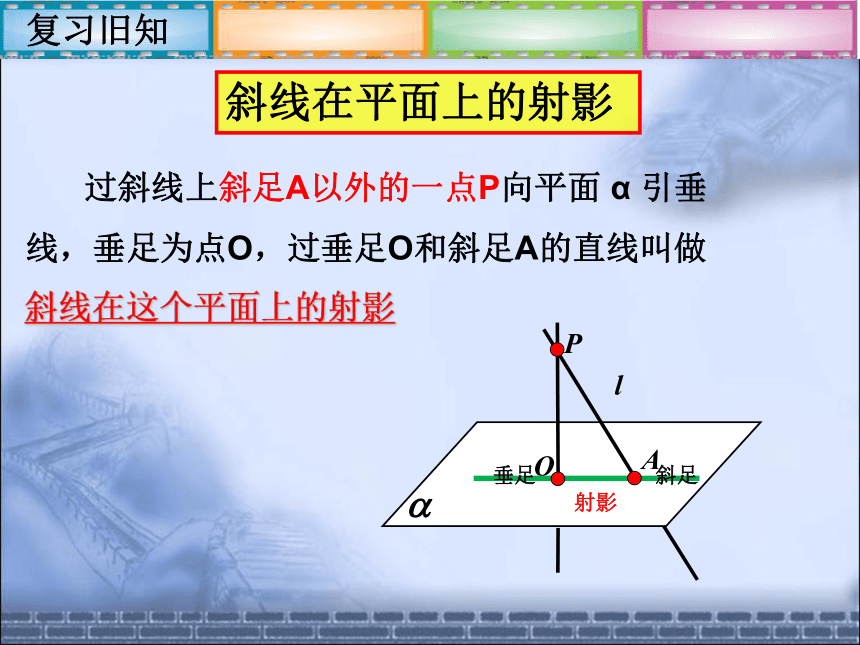
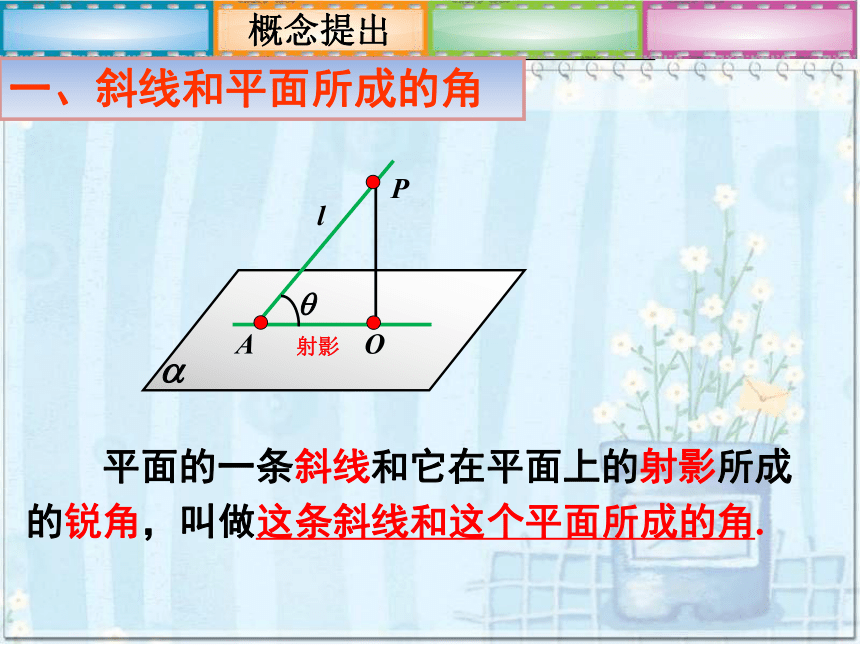
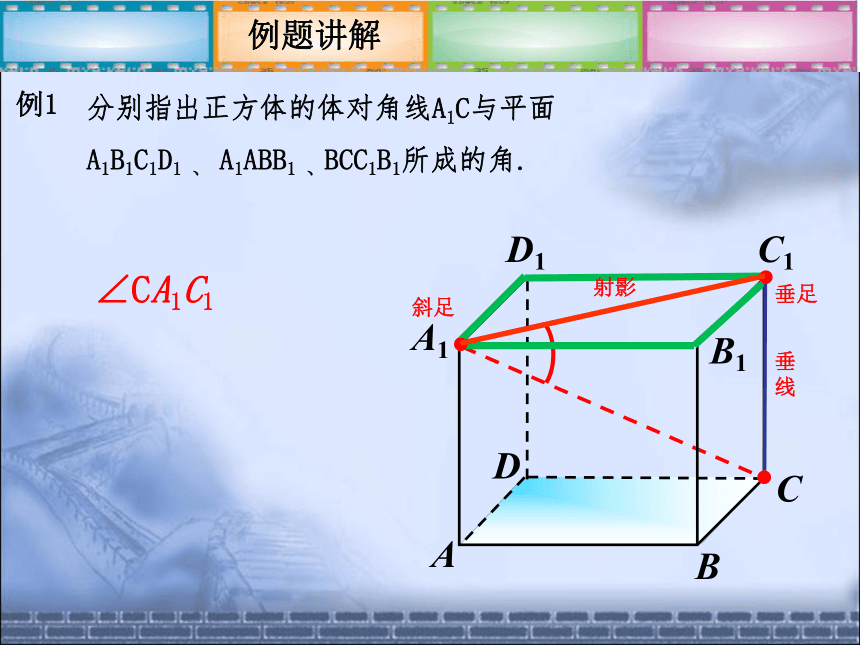
所成的角PAOl垂足斜足复习旧知 过斜线上斜足A以外的一点P向平面 α 引垂线,垂足为点O,过垂足O和斜足A的直线叫做斜线在这个平面上的射影斜线在平面上的射影射影斜足垂足射影斜线垂线他与地面所成的角是哪个角? 平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角.斜线和平面所成的角概念提出一、斜线和平面所成的角PAOl射影例题讲解例1斜足垂足垂线射影分别指出正方体的体对角线A1C与平面 A1B1C1D1 、 A1ABB1 、BCC1B1所成的角.∠CA1C1
分别指出正方体的体对角线A1C与平面 A1B1C1D1 、 A1ABB1 、BCC1B1所成的角.例1例题讲解∠CA1B
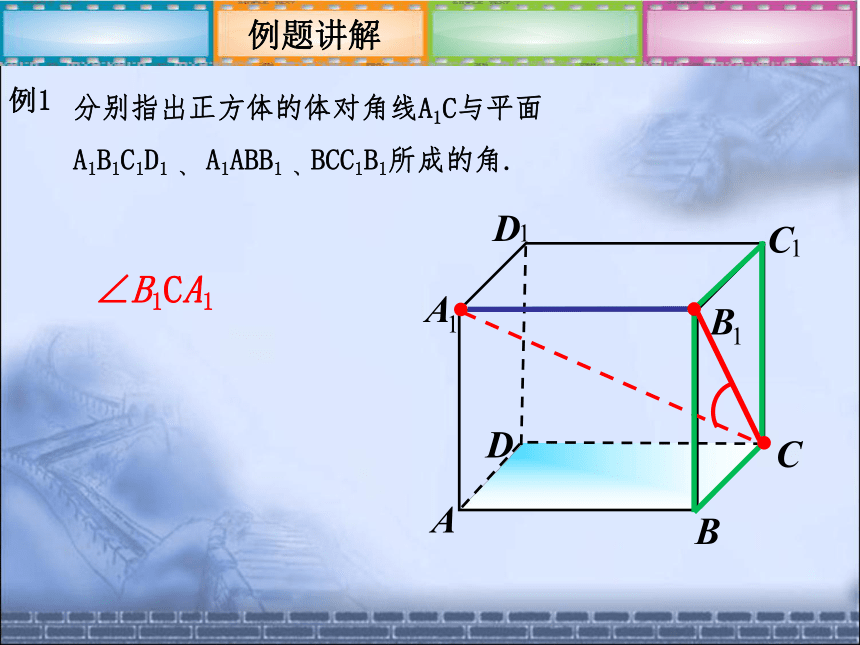
分别指出正方体的体对角线A1C与平面 A1B1C1D1 、 A1ABB1 、BCC1B1所成的角.例1例题讲解∠B1CA1
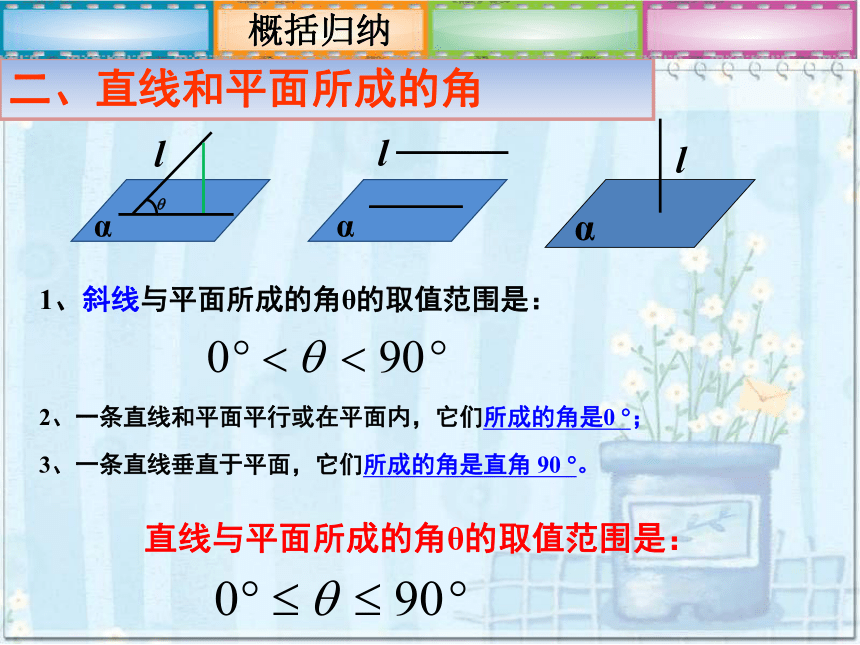
lααl2、一条直线和平面平行或在平面内,它们所成的角是0 ?;3、一条直线垂直于平面,它们所成的角是直角 90 ?。1、斜线与平面所成的角θ的取值范围是: 直线与平面所成的角θ的取值范围是: 二、直线和平面所成的角概括归纳αl练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB0o小试牛刀练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB0o90o小试牛刀练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB0o90o45o小试牛刀练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;0o90o45oADCB90o小试牛刀例2:正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成的角。求角 →找角 →找射影
ABCDA1B1C1D1M典例精讲例2: 正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成的角。设正方体ABCD-A1B1C1D1棱长为a .
如图所示,连接BC1交B1C于M点,连接A1M.
∵ DC ⊥平面BCB1C1
∴ DC ⊥ BC1
∵ BC1 ⊥ B1C, DC ∩ B1C=C
∴ BC1 ⊥ 平面A1B1CD
∴ BM ⊥ 平面A1B1CD
∴A1M 为A1B在平面A1B1CD上的射影.
∴∠BA1M 为A1B与平面A1B1CD所成的角.
在Rt△A1BM 中,A1B= ,BM=
sin∠BA1M= = ,
∴∠BA1M=30°.
即A1B与平面A1B1CD所成的角为30°.
解:ABCDA1B1C1D1M典例精讲通常在垂线和斜线段、射影组成的直角三角形 中计算 。(3)计算:证明某平面角就是斜线和平面所成的角(2)证明:过斜线上一点作平面的垂线,再连结垂足和斜足。 作(或找)出斜线在平面上的射影,将空间角(斜线和平面所成的角) 转化为平面角(两条相交直线所成 的锐角)。AB一“作”二“证”三“计算” 关键:确定斜线在平面内的射影.求直线和平面所成角的方法步骤(1)作图:斜线和射影所成的角就是斜线和平面所成的角。归纳总结射影斜线段垂线2. 求直线和平面所成角的方法1. 直线和平面所成角一“作”二“证”三“计算”课堂小结一、过关训练作业布置星星你谢谢
所成的角Bqr6401@126.com直线和平面
所成的角PAOl垂足斜足复习旧知 过斜线上斜足A以外的一点P向平面 α 引垂线,垂足为点O,过垂足O和斜足A的直线叫做斜线在这个平面上的射影斜线在平面上的射影射影斜足垂足射影斜线垂线他与地面所成的角是哪个角? 平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角.斜线和平面所成的角概念提出一、斜线和平面所成的角PAOl射影例题讲解例1斜足垂足垂线射影分别指出正方体的体对角线A1C与平面 A1B1C1D1 、 A1ABB1 、BCC1B1所成的角.∠CA1C1
分别指出正方体的体对角线A1C与平面 A1B1C1D1 、 A1ABB1 、BCC1B1所成的角.例1例题讲解∠CA1B
分别指出正方体的体对角线A1C与平面 A1B1C1D1 、 A1ABB1 、BCC1B1所成的角.例1例题讲解∠B1CA1
lααl2、一条直线和平面平行或在平面内,它们所成的角是0 ?;3、一条直线垂直于平面,它们所成的角是直角 90 ?。1、斜线与平面所成的角θ的取值范围是: 直线与平面所成的角θ的取值范围是: 二、直线和平面所成的角概括归纳αl练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB0o小试牛刀练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB0o90o小试牛刀练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;ADCB0o90o45o小试牛刀练习1.如图:正方体ABCD-A1B1C1D1中,
(1)求出A1C1与面ABCD所成的角的度数;
(2)求出A1B1与面BCC1B1所成的角的度数;
(3)求出A1C1与面BCC1B1所成的角的度数;
(4)求出A1C1与面BB1D1D所成的角的度数;0o90o45oADCB90o小试牛刀例2:正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成的角。求角 →找角 →找射影
ABCDA1B1C1D1M典例精讲例2: 正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成的角。设正方体ABCD-A1B1C1D1棱长为a .
如图所示,连接BC1交B1C于M点,连接A1M.
∵ DC ⊥平面BCB1C1
∴ DC ⊥ BC1
∵ BC1 ⊥ B1C, DC ∩ B1C=C
∴ BC1 ⊥ 平面A1B1CD
∴ BM ⊥ 平面A1B1CD
∴A1M 为A1B在平面A1B1CD上的射影.
∴∠BA1M 为A1B与平面A1B1CD所成的角.
在Rt△A1BM 中,A1B= ,BM=
sin∠BA1M= = ,
∴∠BA1M=30°.
即A1B与平面A1B1CD所成的角为30°.
解:ABCDA1B1C1D1M典例精讲通常在垂线和斜线段、射影组成的直角三角形 中计算 。(3)计算:证明某平面角就是斜线和平面所成的角(2)证明:过斜线上一点作平面的垂线,再连结垂足和斜足。 作(或找)出斜线在平面上的射影,将空间角(斜线和平面所成的角) 转化为平面角(两条相交直线所成 的锐角)。AB一“作”二“证”三“计算” 关键:确定斜线在平面内的射影.求直线和平面所成角的方法步骤(1)作图:斜线和射影所成的角就是斜线和平面所成的角。归纳总结射影斜线段垂线2. 求直线和平面所成角的方法1. 直线和平面所成角一“作”二“证”三“计算”课堂小结一、过关训练作业布置星星你谢谢
