高考考试大纲解读
图片预览











文档简介
课件64张PPT。高 考 考 试 大 纲 解 读北京工大附中 常毓喜第一部分 2009年高考数学试题分析
第二部分 2010年高考考试大纲解读第一部分 2009年高考数学试题分析一、突出重点,知识覆盖全面二、立足基础、难易布局合理三、强调通法,淡化特殊技巧 突出对主干知识的重点考查,六道大题仍然考的是函数与导数、数列、三角函数、立体几何、解析几何、概率这些重点知识.立体几何着重考查线线关系、线面关系及面面关系中的二面角;解析几何着重考查圆锥曲线.试题注重了知识之间的内在联系,重点内容重点考,知识和能力并重,又有一定的难度和深度,能有效区分不同能力层次的考生群体.一、突出重点,知识覆盖全面 从总体上均做到了由易到难,层次分明.而按题型布局,选择、填空、解答题三大题型内部又由易到难,层次分明;同时解答题仍保持了低起点、宽入口、逐步深入的格局.概率试题命制的的背景(题干部分)相同,而求解的问题不同,文科考查概率的计算,理科考查概率计算的同时还考察了随机变量的分布列及数学期望的求法. 二、立足基础、难易布局合理 试题突出考查常规方法和通性通法,淡化特殊技巧,较好地体现了以知识为载体,以方法为依托,以能力为考查目的的命题导向.全卷没有直接考查纯记忆的陈述性知识,立足基本方法和通性通法,同时在知识的应用上又有一定的灵活性.整卷新题不难,题型常规但不失难度,有助于检测考生对数学学科知识的理解、掌握和运用情况,更有利于优生充分发挥水平,有利于公平竞争.三、强调通法,淡化特殊技巧●考试性质
普通高等学校招生全国统一考试是合格的高中毕业生和具有同等学力的考生参加的选拔性考试.高等学校根据考生成绩,按已确定的招生计划,德、智、体全面衡量,择优录取.因此,高考应具有较高的信度、效度,必要的区分度和适当的难度.第二部分 2010年高考考试大纲解读●考试要求一、命题原则
数学科的考试,按照“考查基础知识的同时,注重考查能力”的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养.
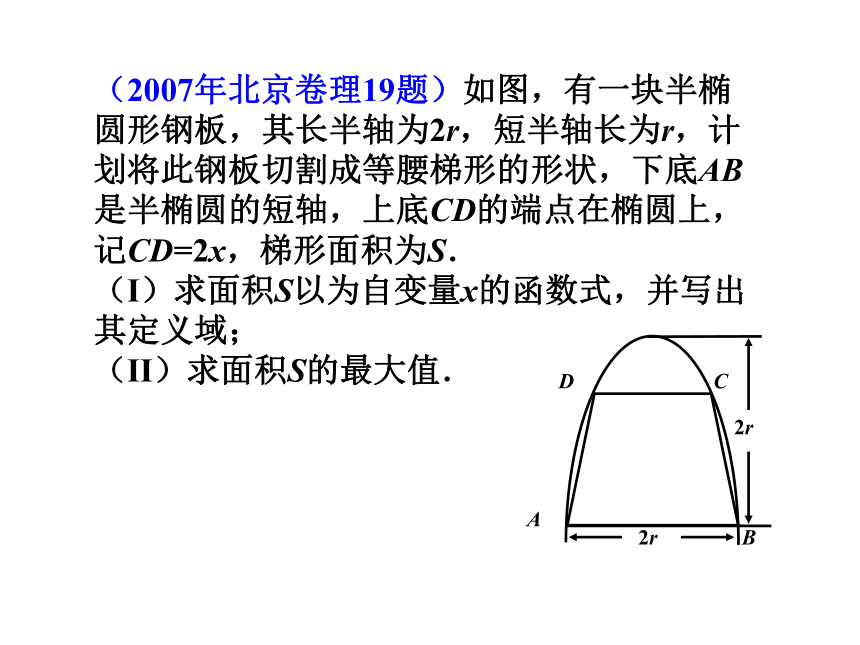
数学科考试要发挥数学作为基础学科的作用,既考查中学数学的知识和方法,又要考查考生进入高校继续学习的潜能.(2007年北京卷理19题)如图,有一块半椭圆形钢板,其长半轴为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
(I)求面积S以为自变量x的函数式,并写出其定义域;
(II)求面积S的最大值.二、考试要求1.知识要求
对数学基础知识的考查,要既全面又突出重点,对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试卷的主体.注重学科的内在联系和知识的综合性,不刻意追求知识的覆盖面.从学科的整体高度和思维价值的高度考虑问题,在知识网络交汇点设计试题,使对数学基础知识的考查达到必要的深度.★ 一是重点内容重点考查(1)函数与导数(2008年全国Ⅱ卷理第22题)
设函数
(Ⅰ)求f(x)的单调区间;
(Ⅱ)如果对任何x≥0,都有f(x)≤ax,求a的取值范围.(2)数列(2008年全国Ⅰ卷理科第20题)设数列{an}的前 n项和为Sn,已知a1=a,an+1=Sn+3n( n∈N*), 设bn=Sn-3n,求数列{bn}的通项.(2008年全国Ⅱ卷理第22题) 设函数 f(x) =x-xlnx.数列{an}满足0(Ⅰ)证明:函数f(x)在区间(0,1)是增函数;
(Ⅱ)证明:an< an+1<1;
(Ⅲ)设b∈(a1,1),整数 证明:ak+1>b.(2009年全国1卷第17题)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2-c2=2b,且sinAcosC=3cosAsinC, 求b.(3)三角函数(2005年全国丙卷理17题)设函数f(x)=sin(2x+?) (-?(Ⅰ)求?;
(Ⅱ)求函数y=f(x)的单调增区间;
(Ⅲ)证明直线5x-2y+c=0与函数y=f(x)的图像不相切. (2007年全国Ⅰ卷第12题)(难度系数:0.466)
函数 的一个单调增区间是(2007年新课程卷第17题)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=?,∠BDC= ?,CD=s,并在点C测得塔顶A的仰角为?,
求塔高AB.(2009年新课程卷第17题)为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内,飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要
测量的数据(用字母表示,
并在图中标出);②用文
字和公式写出计算M,N间
的距离的步骤. (2009年辽宁卷第17题)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75o,30o,于水面C处测得B点和D点的仰角均为60o,AC=0.1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,(4)立体几何 分值约25分左右.在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况.
近三年的立体几何试题,除了2007年全国Ⅰ卷考查了直线与平面所成角外,均重点考查了二面角,而且基本上都是利用三垂线定理找其平面角.(5)解析几何 分值约30分左右.处理解析几何题,学生主要是在“算”上的功夫不够.所谓“算”,主要讲的是算理和算法.算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质.有时候算理和算法并不是截然区分的.在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点.(6)概率与统计(2009年全国1卷第19题)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局.
(I)求甲获得这次比赛胜利的概率;
(II)设?表示从第3局开始到比赛结束所进行的局数,求?的分布列及数学期望.(2008年全国Ⅰ卷理第20题)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(Ⅱ)?表示依方案乙所需化验次数,求? 的期望.(2007年新课程卷第20题)如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为 ,假设正方形ABCD的边长为2, M的面积为1,并向正方形中ABCD随机投掷10000个点,以X表示落入M中的点的数目.
(I)求X的均值EX;
(II)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间(-0.003,0.003)内的概率.(2008年新课程卷第19题)A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1,X2的分布列分别为
(Ⅰ)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得到利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(2009新课程卷理)某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.(i)先确定x,y,再在答题纸上完成下列频率分布直方图.就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表) ★二是加强知识的综合性(2009年全国1卷第22题)设函数f(x)=x3+3bx2+3cx有两个极值点x1, x2,且 x1∈[-1,0], x2∈[1,2].
(I)求b, c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b, c)的区域;
(II)证明:由题意知方程f /(x)=0有两个根x1, x2, 且x1∈[-1,0],x2∈[1,2]. 对数学思想和方法的考查是对数学知识在更高层次上的抽象和概括的考查,考查时必须要与数学知识相结合,通过数学知识的考查,反映考生对数学思想和方法的理解;要从学科整体意义和思想价值立意,注意通性通法,淡化特殊技巧,有效地检测考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度.★三是对基础知识的考查要达到必要的深度(2007年Ⅰ卷理17题文第20题)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围.函数的思想解:(Ⅰ)根据正弦定理得sinA=2sinBsinA,(Ⅱ)cosA+sinC的取值范围是(2009年全国1卷文)设等差数列{an}的前n项和为Sn,公比是正数的等比数列{bn}的前n项和为Tn,已知a1=1,b1=3,a3+b3=17, T3-S3=12,求{an}, {bn}的通项公式.方程的思想数形结合思想xyOBAMNFl 而直线y=-x+2.5与直线y=x-1垂直,所以垂足M为A、B的中点.由于函数y=2x-1与y=log2(x-1)的图象
关于直线y=x-1对称,分类讨论的思想(2009年全国1卷第17题)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2-c2=2b,且sinAcosC=3cosAsinC, 求b.转化与化归的思想B1(2005全国甲卷文理科第4题)设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为
(A)
(B)
(C)
(D)ABCC1A1QP特殊与一般的思想 过抛物线y=ax2(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是p、q,则 等于
A.2a B.1/2a
C.4a D.1/4a(2000年全国新课程理科第11题)xyPQFO有限与无限的思想 一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜。记三种盖法屋顶面积分别为p1、p2、p3. ① ② ③
若屋顶斜面与水平面所成的角都是?,则(2001年全国新课程理科第11题)2.能力要求 对数学能力的考查,强调 “以能力立意”,就是以数学知识为载体,从问题入手,把握学科的整体意义,用统一的数学观点组织材料,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同情景中去的能力,从而检测出考生个体理性思维的广度和深度以及进一步学习的潜能. (1)思维能力
对能力的考查,以思维能力为核心,全面考查各种能力,强调综合性、应用性,并切合考生实际. (2006年北京卷理文8题)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、 C 的机动车辆数如图所示,图中 x1, x2, x3分别表示该时段单位时间通过路段 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则 (A)x1>x2>x3 ? ? (B)x1> x3 > x2
(C)x2 > x3> x1? (D)x3 > x2> x1(2007年广东卷第7题)图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A、B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为
A.18 B.17 C.16 D.15方案一:从A往D调动10件,从C往D调动1件,从B往C调动5件;方案二:从A往D调动11件,从B往A调动1件,从B往C调动4件; 设这四个维修点A,B,C,D处的调动件数分别为xA,xB, xCxD,则有xA≥|50-40|=10, xB≥|50-45|=5,
xC≥|50-54|=4, xD≥|50-61|=11,所以总的调动件数n不小于不相邻的维修点之间调动件数之和,即n≥14且n≥16.y=|x1|+|x2|+|x3|+|x4|=|x1|+|x1+5|+|x1+1|+|x1-10|≥|(x1-10)-(x1+5)|+|(x1+1)-x1|=11+5=16, 当(x1-10)(x1+5)≤0且x1(x1+1)≤0
时等号成立,这时 -1 ≤x1≤ 0. (2006年全国甲卷理12题)A.190 B.171
C.90 D.45 对运算能力的考查主要是对算理和逻辑推理的考查,考查时以代数运算为主,同时也考查估算、简算.(2)运算能力解:根据已知有:所以于是 对空间想象能力的考查,主要体现在对文字语言、符号语言及图形语言三种语言的互相转化,表现为对图形的识别、理解和加工,考查时要与运算能力、逻辑思维能力相结合.(3)空间想象能力(2007年海宁卷理第8题)已知某个几何体的 三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是20 正视图侧视图10俯视图20 20 10谢 谢
2010.3.20
第二部分 2010年高考考试大纲解读第一部分 2009年高考数学试题分析一、突出重点,知识覆盖全面二、立足基础、难易布局合理三、强调通法,淡化特殊技巧 突出对主干知识的重点考查,六道大题仍然考的是函数与导数、数列、三角函数、立体几何、解析几何、概率这些重点知识.立体几何着重考查线线关系、线面关系及面面关系中的二面角;解析几何着重考查圆锥曲线.试题注重了知识之间的内在联系,重点内容重点考,知识和能力并重,又有一定的难度和深度,能有效区分不同能力层次的考生群体.一、突出重点,知识覆盖全面 从总体上均做到了由易到难,层次分明.而按题型布局,选择、填空、解答题三大题型内部又由易到难,层次分明;同时解答题仍保持了低起点、宽入口、逐步深入的格局.概率试题命制的的背景(题干部分)相同,而求解的问题不同,文科考查概率的计算,理科考查概率计算的同时还考察了随机变量的分布列及数学期望的求法. 二、立足基础、难易布局合理 试题突出考查常规方法和通性通法,淡化特殊技巧,较好地体现了以知识为载体,以方法为依托,以能力为考查目的的命题导向.全卷没有直接考查纯记忆的陈述性知识,立足基本方法和通性通法,同时在知识的应用上又有一定的灵活性.整卷新题不难,题型常规但不失难度,有助于检测考生对数学学科知识的理解、掌握和运用情况,更有利于优生充分发挥水平,有利于公平竞争.三、强调通法,淡化特殊技巧●考试性质
普通高等学校招生全国统一考试是合格的高中毕业生和具有同等学力的考生参加的选拔性考试.高等学校根据考生成绩,按已确定的招生计划,德、智、体全面衡量,择优录取.因此,高考应具有较高的信度、效度,必要的区分度和适当的难度.第二部分 2010年高考考试大纲解读●考试要求一、命题原则
数学科的考试,按照“考查基础知识的同时,注重考查能力”的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养.
数学科考试要发挥数学作为基础学科的作用,既考查中学数学的知识和方法,又要考查考生进入高校继续学习的潜能.(2007年北京卷理19题)如图,有一块半椭圆形钢板,其长半轴为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
(I)求面积S以为自变量x的函数式,并写出其定义域;
(II)求面积S的最大值.二、考试要求1.知识要求
对数学基础知识的考查,要既全面又突出重点,对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试卷的主体.注重学科的内在联系和知识的综合性,不刻意追求知识的覆盖面.从学科的整体高度和思维价值的高度考虑问题,在知识网络交汇点设计试题,使对数学基础知识的考查达到必要的深度.★ 一是重点内容重点考查(1)函数与导数(2008年全国Ⅱ卷理第22题)
设函数
(Ⅰ)求f(x)的单调区间;
(Ⅱ)如果对任何x≥0,都有f(x)≤ax,求a的取值范围.(2)数列(2008年全国Ⅰ卷理科第20题)设数列{an}的前 n项和为Sn,已知a1=a,an+1=Sn+3n( n∈N*), 设bn=Sn-3n,求数列{bn}的通项.(2008年全国Ⅱ卷理第22题) 设函数 f(x) =x-xlnx.数列{an}满足0
(Ⅱ)证明:an< an+1<1;
(Ⅲ)设b∈(a1,1),整数 证明:ak+1>b.(2009年全国1卷第17题)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2-c2=2b,且sinAcosC=3cosAsinC, 求b.(3)三角函数(2005年全国丙卷理17题)设函数f(x)=sin(2x+?) (-?
(Ⅱ)求函数y=f(x)的单调增区间;
(Ⅲ)证明直线5x-2y+c=0与函数y=f(x)的图像不相切. (2007年全国Ⅰ卷第12题)(难度系数:0.466)
函数 的一个单调增区间是(2007年新课程卷第17题)如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=?,∠BDC= ?,CD=s,并在点C测得塔顶A的仰角为?,
求塔高AB.(2009年新课程卷第17题)为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内,飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要
测量的数据(用字母表示,
并在图中标出);②用文
字和公式写出计算M,N间
的距离的步骤. (2009年辽宁卷第17题)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75o,30o,于水面C处测得B点和D点的仰角均为60o,AC=0.1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,(4)立体几何 分值约25分左右.在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况.
近三年的立体几何试题,除了2007年全国Ⅰ卷考查了直线与平面所成角外,均重点考查了二面角,而且基本上都是利用三垂线定理找其平面角.(5)解析几何 分值约30分左右.处理解析几何题,学生主要是在“算”上的功夫不够.所谓“算”,主要讲的是算理和算法.算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质.有时候算理和算法并不是截然区分的.在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点.(6)概率与统计(2009年全国1卷第19题)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局.
(I)求甲获得这次比赛胜利的概率;
(II)设?表示从第3局开始到比赛结束所进行的局数,求?的分布列及数学期望.(2008年全国Ⅰ卷理第20题)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(Ⅱ)?表示依方案乙所需化验次数,求? 的期望.(2007年新课程卷第20题)如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为 ,假设正方形ABCD的边长为2, M的面积为1,并向正方形中ABCD随机投掷10000个点,以X表示落入M中的点的数目.
(I)求X的均值EX;
(II)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间(-0.003,0.003)内的概率.(2008年新课程卷第19题)A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1,X2的分布列分别为
(Ⅰ)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;
(Ⅱ)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得到利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(2009新课程卷理)某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.(i)先确定x,y,再在答题纸上完成下列频率分布直方图.就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表) ★二是加强知识的综合性(2009年全国1卷第22题)设函数f(x)=x3+3bx2+3cx有两个极值点x1, x2,且 x1∈[-1,0], x2∈[1,2].
(I)求b, c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b, c)的区域;
(II)证明:由题意知方程f /(x)=0有两个根x1, x2, 且x1∈[-1,0],x2∈[1,2]. 对数学思想和方法的考查是对数学知识在更高层次上的抽象和概括的考查,考查时必须要与数学知识相结合,通过数学知识的考查,反映考生对数学思想和方法的理解;要从学科整体意义和思想价值立意,注意通性通法,淡化特殊技巧,有效地检测考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度.★三是对基础知识的考查要达到必要的深度(2007年Ⅰ卷理17题文第20题)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围.函数的思想解:(Ⅰ)根据正弦定理得sinA=2sinBsinA,(Ⅱ)cosA+sinC的取值范围是(2009年全国1卷文)设等差数列{an}的前n项和为Sn,公比是正数的等比数列{bn}的前n项和为Tn,已知a1=1,b1=3,a3+b3=17, T3-S3=12,求{an}, {bn}的通项公式.方程的思想数形结合思想xyOBAMNFl 而直线y=-x+2.5与直线y=x-1垂直,所以垂足M为A、B的中点.由于函数y=2x-1与y=log2(x-1)的图象
关于直线y=x-1对称,分类讨论的思想(2009年全国1卷第17题)在△ABC中,内角A、B、C的对边长分别为a、b、c,已知a2-c2=2b,且sinAcosC=3cosAsinC, 求b.转化与化归的思想B1(2005全国甲卷文理科第4题)设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为
(A)
(B)
(C)
(D)ABCC1A1QP特殊与一般的思想 过抛物线y=ax2(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是p、q,则 等于
A.2a B.1/2a
C.4a D.1/4a(2000年全国新课程理科第11题)xyPQFO有限与无限的思想 一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜。记三种盖法屋顶面积分别为p1、p2、p3. ① ② ③
若屋顶斜面与水平面所成的角都是?,则(2001年全国新课程理科第11题)2.能力要求 对数学能力的考查,强调 “以能力立意”,就是以数学知识为载体,从问题入手,把握学科的整体意义,用统一的数学观点组织材料,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同情景中去的能力,从而检测出考生个体理性思维的广度和深度以及进一步学习的潜能. (1)思维能力
对能力的考查,以思维能力为核心,全面考查各种能力,强调综合性、应用性,并切合考生实际. (2006年北京卷理文8题)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、 C 的机动车辆数如图所示,图中 x1, x2, x3分别表示该时段单位时间通过路段 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则 (A)x1>x2>x3 ? ? (B)x1> x3 > x2
(C)x2 > x3> x1? (D)x3 > x2> x1(2007年广东卷第7题)图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A、B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为
A.18 B.17 C.16 D.15方案一:从A往D调动10件,从C往D调动1件,从B往C调动5件;方案二:从A往D调动11件,从B往A调动1件,从B往C调动4件; 设这四个维修点A,B,C,D处的调动件数分别为xA,xB, xCxD,则有xA≥|50-40|=10, xB≥|50-45|=5,
xC≥|50-54|=4, xD≥|50-61|=11,所以总的调动件数n不小于不相邻的维修点之间调动件数之和,即n≥14且n≥16.y=|x1|+|x2|+|x3|+|x4|=|x1|+|x1+5|+|x1+1|+|x1-10|≥|(x1-10)-(x1+5)|+|(x1+1)-x1|=11+5=16, 当(x1-10)(x1+5)≤0且x1(x1+1)≤0
时等号成立,这时 -1 ≤x1≤ 0. (2006年全国甲卷理12题)A.190 B.171
C.90 D.45 对运算能力的考查主要是对算理和逻辑推理的考查,考查时以代数运算为主,同时也考查估算、简算.(2)运算能力解:根据已知有:所以于是 对空间想象能力的考查,主要体现在对文字语言、符号语言及图形语言三种语言的互相转化,表现为对图形的识别、理解和加工,考查时要与运算能力、逻辑思维能力相结合.(3)空间想象能力(2007年海宁卷理第8题)已知某个几何体的 三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是20 正视图侧视图10俯视图20 20 10谢 谢
2010.3.20
同课章节目录
