研究高考试题,探索复习策略
图片预览










文档简介
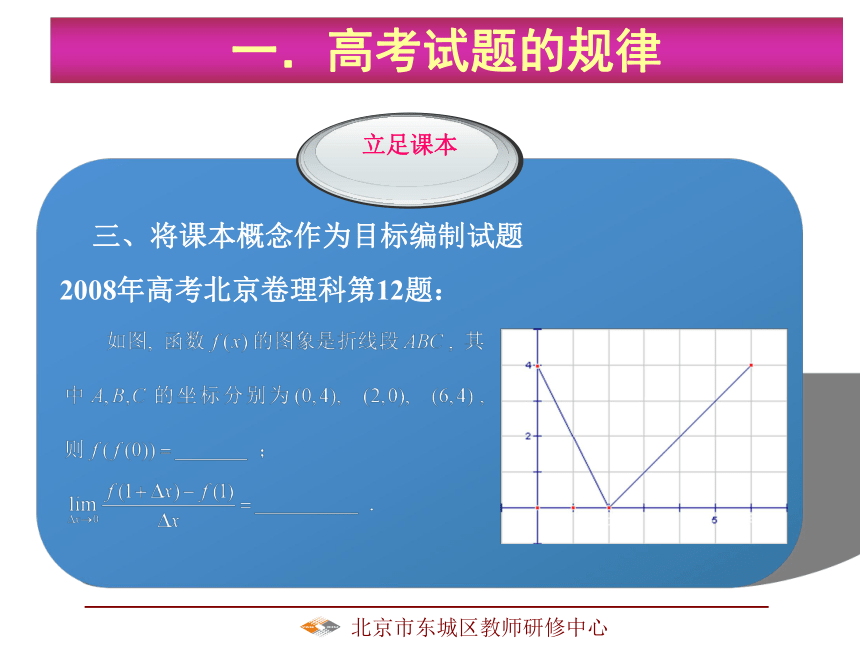
课件174张PPT。 研究高考试题,探索复习策略 2010年3月13日北京东城教师研修中心 雷晓莉 北京市东城区教师研修中心(1)对高考题的分析与研究(2)对高考试题的深入解读(3)对高考命题的基本了解(4)对复习方法的选择(5)对复习用书与复习用题的选择研究高考试题,探索复习策略 北京市东城区教师研修中心.研究高考试题,探索复习策略 北京市东城区教师研修中心,.一.高考试题的规律立足课本一、将课本题目改变题型编制试题 北京市东城区教师研修中心,.立足课本二、将课本题目改变数字编制试题一.高考试题的规律2009全国2卷文科 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律2009全国2卷理科 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本三、将课本概念作为目标编制试题2008年高考北京卷理科第12题:一.高考试题的规律 北京市东城区教师研修中心,.立足课本体现函数概念的试题 (2007年北京卷理科14) 一.高考试题的规律 北京市东城区教师研修中心,.立足课本体现函数概念的试题 (2006年山东卷文科2) 一.高考试题的规律 北京市东城区教师研修中心,.立足课本体现导数概念的试题 (2006年重庆卷理科20) 一.高考试题的规律 北京市东城区教师研修中心,.立足课本体现导数概念的试题 (2006年重庆卷理科20) 一.高考试题的规律 北京市东城区教师研修中心,.立足课本体现导数概念的试题 (2006年全国卷II理科20)一.高考试题的规律 北京市东城区教师研修中心,.立足课本体现导数概念的试题 一.高考试题的规律 北京市东城区教师研修中心,.立足课本体现导数概念的试题 一.高考试题的规律 北京市东城区教师研修中心.一.高考试题的规律09广东理科(8)考查定积分概念 北京市东城区教师研修中心.一.高考试题的规律09全国1卷理科(11) 北京市东城区教师研修中心.一.高考试题的规律09海南卷理科(2) 北京市东城区教师研修中心.一.高考试题的规律 北京市东城区教师研修中心.一.高考试题的规律 北京市东城区教师研修中心.一.高考试题的规律 北京市东城区教师研修中心一.高考试题的规律 北京市东城区教师研修中心,.立足课本四、将课本题目加以拓广编制试题一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本五、将课本情景作为背景编制试题一.高考试题的规律 北京市东城区教师研修中心,.立足课本原型题::人教版第二册(上)P91 章头图“圆锥曲线是我们生活中常见的曲线,
例如倾斜着的圆柱形水杯的水面的边界线,
汽车油罐截面的轮廓线,………. 一.高考试题的规律 北京市东城区教师研修中心,.立足课本例2008年湖北卷(理科10) 一.高考试题的规律 北京市东城区教师研修中心,.立足课本原型题::人教版第二册(上)P99 例3 我国发射的第一颗人造地球卫星的运行轨道是以地心为一个焦点的椭圆,已知它的近地点A距地面439千米,远地点B距地面2384千米,并且、A、B在同一直线上,地球半径约为6371千米,求卫星运行的轨道方程。一.高考试题的规律 北京市东城区教师研修中心,.立足课本人教版第二册(上)P103习题8.2 彗星“紫金山一号”是南京天文台发现的,它的运行轨道是以太阳为一个焦点的椭圆,测得轨道的近日点距太阳中心1.486天文单位,远日点距太阳中心5.563天文单位,近日点、远日点及太阳中心在同一直线上,求轨道方程。一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本六、将课本题目结论作为背景编制试题一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 ,.二.二轮复习的思路怎样立足课本以《函数》为例进行说明 北京市东城区教师研修中心.二.二轮复习的思路(一) 高考考查的三个层次 1.全面考查基础知识(1)2009年广东卷文(4)(一) 高考考查的三个层次 1.全面考查基础知识(2)2009广东卷理(3)(一) 高考考查的三个层次 1.全面考查基础知识(3)2009全国2卷文科(3) (一) 高考考查的三个层次 1.全面考查基础知识(4)2009全国1卷理科(7) (一) 高考考查的三个层次 1.全面考查基础知识(5)2009辽宁卷文科(6)(一) 高考考查的三个层次 2.突出考查思想方法(1)2009辽宁卷理科(9)(一) 高考考查的三个层次 2.突出考查思想方法(2)2009海南宁夏卷理科(12) (一) 高考考查的三个层次 3.深入考查数学能力(1)2009辽宁卷理科(12)(一) 高考考查的三个层次 3.深入考查数学能力(2)2008北京卷理科(13)(一) 高考考查的三个层次 3.深入考查数学能力(3)2009全国1卷理科(11)(二) 复习注意的五个问题 (一)深入理解概念单调性与凹凸性。注意联系与发展:奇偶性与对称性;对称性与周期性;(二) 复习注意的五个问题 (一)深入理解概念 函数的概念(一)深入理解概念 函数的概念(1)(2007年北京卷理科14) (二) 复习注意的五个问题 (一)深入理解概念 函数的概念(2)(2006年山东卷文科2)(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解(1)函数在给定区间上的单调性,反映了函数在区间上的函数值的变化趋势,是函数在区间上的整体性质,但不一定是函数在定义域上的整体性质 (2)对于某个具体函数的单调区间,可以是整个定义域(如一次函数),可以是定义域内某个区间(如二次函数),也可以根本不单调(如常函数).同一个函数在不同的区间上可有不同的单调性.(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解09浙江理科22(二) 复习注意的五个问题 (二) 复习注意的五个问题 方法二(二) 复习注意的五个问题 方法三结合图象可知 -5b),
则,f(x+2a-2b)=f[a+(x+a-2b)] (恒等变形)
=f[a-(x+a-2b)] [f(a+x)=f(a-x)]
= f(-x+2b) (恒等变形)
=f[b+(-x+b)] (恒等变形)
=f[b-(-x+b)] [ f(b+x)=f(b-x)]
=f(x)T=2a-2b(二) 学习注意的五个问题 又如:若f(a+x)= -f(a-x), f(b+x)= -f(b-x),
则,f(x+2a-2b)=f[a+(x+a-2b)] (恒等变形)
= -f[a-(x+a-2b)] [f(a+x)=-f(a-x)]
= - f(-x+2b) (恒等变形)
= -f[b+(-x+b)] (恒等变形)
=+f[b-(-x+b)] [ f(b+x)=-f(b-x)]
=f(x)T=2a-2b(二) 学习注意的五个问题 又如:若f(a+x)= -f(a-x), f(b+x)= f(b-x),
则,f(x+2a-2b)=f[a+(x+a-2b)] (恒等变形)
= -f[a-(x+a-2b)] [f(a+x)=-f(a-x)]
= - f(-x+2b) (恒等变形)
= -f[b+(-x+b)] (恒等变形)
=-f[b-(-x+b)] [ f(b+x)=f(b-x)]
=-f(x) 2a-2b为半周期(二) 学习注意的五个问题 单调性任取x1,x2∈D,且x1有y1y=f(x)在D上为增函数; 若函数f(x)的导函数 在D上的函数值
为正,则称y=f(x)在D上为增函数;(二) 复习注意的五个问题 单调性与凹凸性(二) 复习注意的五个问题 凹凸性(二) 复习注意的五个问题 中点定比分点 若函数f(x)的导函数 在D上的函数值
为正,则称y=f(x)在D上为上凹函数.(二) 学习注意的五个问题 (一)深入理解概念例1: 1994年全国卷(理22)(二) 复习注意的五个问题 (一)深入理解概念例2: 1994年全国卷(文22)(二) 复习注意的五个问题 (一)深入理解概念例3: 2005年北京卷(理13)(二) 复习注意的五个问题 北京市东城区教师研修中心.函数概念性质的综合理解 (二) 复习注意的五个问题 北京市东城区教师研修中心.(1)的思考 (二) 复习注意的五个问题 北京市东城区教师研修中心.(1)“ 恒过定点”这里“ 恒” 的含义是什么?思考:(二) 复习注意的五个问题 北京市东城区教师研修中心.(2)(二) 复习注意的五个问题 北京市东城区教师研修中心.(二) 复习注意的五个问题 北京市东城区教师研修中心.(2)复习基础知识, 基本方法应遵循的原则① 用概念规范和引领思维活动② 对基本概念, 基本理论要本着“ 强化理性思维” ,
帮助学生“ 认识数学的本质” 的原则, 多角度、
全方位地做深人浅出的剖析(二) 复习注意的五个问题 北京市东城区教师研修中心.③ 有联系的知识网络, 通过概念的内涵和逻辑的
“叠加” , 达到相互联系、融汇变通例如:函数的单调性(二) 复习注意的五个问题 北京市东城区教师研修中心.(二) 复习注意的五个问题 北京市东城区教师研修中心.函数的奇偶性问(2):上述两种说法中, 哪一种容易推广,推广后,
得到了一个怎样的命题?(二) 复习注意的五个问题 北京市东城区教师研修中心.(3) 解题教学应遵循的基本原则(二) 复习注意的五个问题 北京市东城区教师研修中心.(二) 复习注意的五个问题 北京市东城区教师研修中心.1.函数与方程的联系(1)2009山东理科卷(14)(二) 复习注意的五个问题 北京市东城区教师研修中心.(2)2009福建文科卷(11) g(0)= -1 (二) 复习注意的五个问题 2.函数与不等式的联系(二) 复习注意的五个问题 解不等式函数的最值解不等式(二) 复习注意的五个问题 (二) 复习注意的五个问题 (二) 复习注意的五个问题 解关于x的不等式解关于c的不等式
求函数的最值(二) 复习注意的五个问题 拆分变量主元处理(二) 复习注意的五个问题 例1(2006年江西卷)若不等式
x2+ax+1?0对于一切x?(0,0.5)
成立,则a的取值范围是( )(二) 复习注意的五个问题 北京市东城区教师研修中心.1.解题之前重在分析2009山东理科(10)(二) 复习注意的五个问题 北京市东城区教师研修中心2009山东理科(16)(二) 复习注意的五个问题 北京市东城区教师研修中心.例: 2006年全国卷2(理)2.解题之后重在总结(二) 复习注意的五个问题 北京市东城区教师研修中心.依次类推(三) 解题过程三步曲 北京市东城区教师研修中心.(二) 复习注意的五个问题 模拟题训练 三.模拟试卷的处理 处理好套题与类题的关系2.处理好难题与容易题的关系3.处理好新题与成题的关系4.处理好梳理知识与作题的关系三.模拟试卷的处理 我们先让学生自己分析试卷,在分析的过程中完成以下两个表格,并在此基础上写出一份简要的小结,分析存在的问题和今后努力的方向。
具体做法1、自主分析环节三.模拟试卷的处理试卷分析表一:(注:15题---20题为解答题)三.模拟试卷的处理试卷分析表二:三.模拟试卷的处理 在自愿的基础上请两位同学根据课前的分
析对自己的考试做一个简要的总结,重点谈
谈考试中的得失,学习中存在的问题及改进
的措施,教师根据情况作适当的点评。
教师进一步用数据说话.
2.统一讲评环节2.1考情分析三.模拟试卷的处理(一)总体情况分析:数据表格一三.模拟试卷的处理三.模拟试卷的处理数据表格二三.模拟试卷的处理三.模拟试卷的处理三.模拟试卷的处理数据表格三三.模拟试卷的处理三.模拟试卷的处理 在试题分析时,并不按照试题的先后顺序讲评,而是按照知识块的划分将只是相近的试题放在一起进行讲评,对重点试题进行重点讲评。现就我们区2005年高三一模数学试卷中的函数与导数内容为例,具体谈谈如何充分发挥数学模拟试卷的功效。
2.2试题分析三.模拟试卷的处理三.模拟试卷的处理(1)以导数为工具考查函数和不等式(2)以导数为载体考查数学思想方法三.模拟试卷的处理三.模拟试卷的处理三.模拟试卷的处理练习 、g(x)分别是定义在R上的奇函数、偶函数,且 上时, , 是锐角三角形的两个锐角且 ,则下列不等式正确的是( ) (A) (B) (C) (D)三.模拟试卷的处理利用导数求函数单调区间的步骤:
(1)正确求导;
(2)确定可疑极值点,并划分区间;
(3)判断各区间的单调性。三.模拟试卷的处理三.模拟试卷的处理公式出错三.模拟试卷的处理运算出错三.模拟试卷的处理三.模拟试卷的处理二.模拟试卷的处理三.模拟试卷的处理未讨论开口方向三.模拟试卷的处理三.模拟试卷的处理区间不能取并集三.模拟试卷的处理分类讨论值得注意的问题:
(1)明确分类讨论的原因;
(2)确定分类的标准;
(3)理清分类的层次;
(4)注意分类结果的整合。三.模拟试卷的处理 ① 与模拟试卷中的文科试题的比较:
已知一、试题分析二、错误分析三、同类比较三.模拟试卷的处理②与高考试题的比较:
(2004年全国A卷理科)已知已知a ,
求函数 的单调区间.
(2004年湖南理科)已知函数 ,
其中a,e为自然数对数的底数.
(I)讨论函数 的单调区间;
(II)求函数 的在区间[0,1]上的最
大值
三.模拟试卷的处理(2005年山东)三.模拟试卷的处理(2006年湖北理科)三.模拟试卷的处理三.模拟试卷的处理(2006年湖北文科)
三.模拟试卷的处理(2006年山东)
(2006年湖南)三.模拟试卷的处理(2007年安徽)
(2007年陕西)三.模拟试卷的处理四、问题深化 以此题为载体,进行条件和结论的变化,使学生在试题变化中、在矛盾斗争冲突中来调整自己的思路,达到举一反三、触类旁通的效果。三.模拟试卷的处理
例1:已知m ,研究函数
的极大值和极小值.题型一三.模拟试卷的处理题型二例2:已知m ,若函数
在 上为单调增函数,求m的取值范围.例3:已知函数 ,
若f (x)在区间(-2,-1)上是增函数,在区间
(3,4)上是减函数,求m的取值范围.三.模拟试卷的处理例4:已知a ,函数 ,
其中e是自然对数的底数.
(I) 判断f(x)在R上的单调性
(II) 是否存在a ,使得f(x)在[1,2]上的最
小值为 .题型三三.模拟试卷的处理五、问题反思 (1) 对知识掌握的反思
(2) 对数学思想方法的反思
(3) 对自己错误的反思
首先我们应该找出自己的错误,是公式出错?运算出错?分类讨论出错?还是对讨论结果的整合出错。出现错误并不可怕,可怕的是自己安慰自己,以“不小心”进行掩盖,而是要从知识上、方法上找原因,要让自己长记性。三.模拟试卷的处理Concept 第三阶段
(5月底~高考)
三.模拟试卷的处理模拟题训练 四.最后阶段的复习一、“忆”
“忆”是对已复习过的课本内容“过电影”,也就是重新回忆一遍。“忆”的内容主要是教材的知识网络、主干知识、重点和难点。回忆基础知识时切忌零散无序,而要强调知识的结构性与整体性,加强各知识点之间的联系,形成知识网络。这种回忆不仅有利于记忆,更重要的是有利于检索和应用。我们以数列的基础知识为例,边忆边写,使淡漠的或遗忘的内容再一次强化。四.最后阶段的复习 等差、等比数列知识归纳
等差数列:(一)基础知识四.最后阶段的复习(二)深化内容
1.函数思想四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习二、“看”
“看”是以阅读的方式进行复习。在最后阶段需要看的内容较多,同学们可以从以下三方面着手。四.最后阶段的复习 看看延伸或补充的内容看已经做过的题看曾经出现过的错误四.最后阶段的复习例如与函数有关的补充定理有: 四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习 北京市东城区教师研修中心Thank You !不足之处恳请大家批评指正研究高考试题,探索复习策略 雷晓莉联系方式:
单位:北京东城教师研修中心数学组
地址:交道口东公街9号
邮编:100009
Tel:84010991(o)
13651227381
Email:leixiaoli03@yahoo.com.cn研究高考试题,探索复习策略
例如倾斜着的圆柱形水杯的水面的边界线,
汽车油罐截面的轮廓线,………. 一.高考试题的规律 北京市东城区教师研修中心,.立足课本例2008年湖北卷(理科10) 一.高考试题的规律 北京市东城区教师研修中心,.立足课本原型题::人教版第二册(上)P99 例3 我国发射的第一颗人造地球卫星的运行轨道是以地心为一个焦点的椭圆,已知它的近地点A距地面439千米,远地点B距地面2384千米,并且、A、B在同一直线上,地球半径约为6371千米,求卫星运行的轨道方程。一.高考试题的规律 北京市东城区教师研修中心,.立足课本人教版第二册(上)P103习题8.2 彗星“紫金山一号”是南京天文台发现的,它的运行轨道是以太阳为一个焦点的椭圆,测得轨道的近日点距太阳中心1.486天文单位,远日点距太阳中心5.563天文单位,近日点、远日点及太阳中心在同一直线上,求轨道方程。一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本六、将课本题目结论作为背景编制试题一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 北京市东城区教师研修中心,.立足课本一.高考试题的规律 ,.二.二轮复习的思路怎样立足课本以《函数》为例进行说明 北京市东城区教师研修中心.二.二轮复习的思路(一) 高考考查的三个层次 1.全面考查基础知识(1)2009年广东卷文(4)(一) 高考考查的三个层次 1.全面考查基础知识(2)2009广东卷理(3)(一) 高考考查的三个层次 1.全面考查基础知识(3)2009全国2卷文科(3) (一) 高考考查的三个层次 1.全面考查基础知识(4)2009全国1卷理科(7) (一) 高考考查的三个层次 1.全面考查基础知识(5)2009辽宁卷文科(6)(一) 高考考查的三个层次 2.突出考查思想方法(1)2009辽宁卷理科(9)(一) 高考考查的三个层次 2.突出考查思想方法(2)2009海南宁夏卷理科(12) (一) 高考考查的三个层次 3.深入考查数学能力(1)2009辽宁卷理科(12)(一) 高考考查的三个层次 3.深入考查数学能力(2)2008北京卷理科(13)(一) 高考考查的三个层次 3.深入考查数学能力(3)2009全国1卷理科(11)(二) 复习注意的五个问题 (一)深入理解概念单调性与凹凸性。注意联系与发展:奇偶性与对称性;对称性与周期性;(二) 复习注意的五个问题 (一)深入理解概念 函数的概念(一)深入理解概念 函数的概念(1)(2007年北京卷理科14) (二) 复习注意的五个问题 (一)深入理解概念 函数的概念(2)(2006年山东卷文科2)(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解(1)函数在给定区间上的单调性,反映了函数在区间上的函数值的变化趋势,是函数在区间上的整体性质,但不一定是函数在定义域上的整体性质 (2)对于某个具体函数的单调区间,可以是整个定义域(如一次函数),可以是定义域内某个区间(如二次函数),也可以根本不单调(如常函数).同一个函数在不同的区间上可有不同的单调性.(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解(二) 复习注意的五个问题 (一)深入理解概念2.对函数单调性的理解09浙江理科22(二) 复习注意的五个问题 (二) 复习注意的五个问题 方法二(二) 复习注意的五个问题 方法三结合图象可知 -5
则,f(x+2a-2b)=f[a+(x+a-2b)] (恒等变形)
=f[a-(x+a-2b)] [f(a+x)=f(a-x)]
= f(-x+2b) (恒等变形)
=f[b+(-x+b)] (恒等变形)
=f[b-(-x+b)] [ f(b+x)=f(b-x)]
=f(x)T=2a-2b(二) 学习注意的五个问题 又如:若f(a+x)= -f(a-x), f(b+x)= -f(b-x),
则,f(x+2a-2b)=f[a+(x+a-2b)] (恒等变形)
= -f[a-(x+a-2b)] [f(a+x)=-f(a-x)]
= - f(-x+2b) (恒等变形)
= -f[b+(-x+b)] (恒等变形)
=+f[b-(-x+b)] [ f(b+x)=-f(b-x)]
=f(x)T=2a-2b(二) 学习注意的五个问题 又如:若f(a+x)= -f(a-x), f(b+x)= f(b-x),
则,f(x+2a-2b)=f[a+(x+a-2b)] (恒等变形)
= -f[a-(x+a-2b)] [f(a+x)=-f(a-x)]
= - f(-x+2b) (恒等变形)
= -f[b+(-x+b)] (恒等变形)
=-f[b-(-x+b)] [ f(b+x)=f(b-x)]
=-f(x) 2a-2b为半周期(二) 学习注意的五个问题 单调性任取x1,x2∈D,且x1
为正,则称y=f(x)在D上为增函数;(二) 复习注意的五个问题 单调性与凹凸性(二) 复习注意的五个问题 凹凸性(二) 复习注意的五个问题 中点定比分点 若函数f(x)的导函数 在D上的函数值
为正,则称y=f(x)在D上为上凹函数.(二) 学习注意的五个问题 (一)深入理解概念例1: 1994年全国卷(理22)(二) 复习注意的五个问题 (一)深入理解概念例2: 1994年全国卷(文22)(二) 复习注意的五个问题 (一)深入理解概念例3: 2005年北京卷(理13)(二) 复习注意的五个问题 北京市东城区教师研修中心.函数概念性质的综合理解 (二) 复习注意的五个问题 北京市东城区教师研修中心.(1)的思考 (二) 复习注意的五个问题 北京市东城区教师研修中心.(1)“ 恒过定点”这里“ 恒” 的含义是什么?思考:(二) 复习注意的五个问题 北京市东城区教师研修中心.(2)(二) 复习注意的五个问题 北京市东城区教师研修中心.(二) 复习注意的五个问题 北京市东城区教师研修中心.(2)复习基础知识, 基本方法应遵循的原则① 用概念规范和引领思维活动② 对基本概念, 基本理论要本着“ 强化理性思维” ,
帮助学生“ 认识数学的本质” 的原则, 多角度、
全方位地做深人浅出的剖析(二) 复习注意的五个问题 北京市东城区教师研修中心.③ 有联系的知识网络, 通过概念的内涵和逻辑的
“叠加” , 达到相互联系、融汇变通例如:函数的单调性(二) 复习注意的五个问题 北京市东城区教师研修中心.(二) 复习注意的五个问题 北京市东城区教师研修中心.函数的奇偶性问(2):上述两种说法中, 哪一种容易推广,推广后,
得到了一个怎样的命题?(二) 复习注意的五个问题 北京市东城区教师研修中心.(3) 解题教学应遵循的基本原则(二) 复习注意的五个问题 北京市东城区教师研修中心.(二) 复习注意的五个问题 北京市东城区教师研修中心.1.函数与方程的联系(1)2009山东理科卷(14)(二) 复习注意的五个问题 北京市东城区教师研修中心.(2)2009福建文科卷(11) g(0)= -1 (二) 复习注意的五个问题 2.函数与不等式的联系(二) 复习注意的五个问题 解不等式函数的最值解不等式(二) 复习注意的五个问题 (二) 复习注意的五个问题 (二) 复习注意的五个问题 解关于x的不等式解关于c的不等式
求函数的最值(二) 复习注意的五个问题 拆分变量主元处理(二) 复习注意的五个问题 例1(2006年江西卷)若不等式
x2+ax+1?0对于一切x?(0,0.5)
成立,则a的取值范围是( )(二) 复习注意的五个问题 北京市东城区教师研修中心.1.解题之前重在分析2009山东理科(10)(二) 复习注意的五个问题 北京市东城区教师研修中心2009山东理科(16)(二) 复习注意的五个问题 北京市东城区教师研修中心.例: 2006年全国卷2(理)2.解题之后重在总结(二) 复习注意的五个问题 北京市东城区教师研修中心.依次类推(三) 解题过程三步曲 北京市东城区教师研修中心.(二) 复习注意的五个问题 模拟题训练 三.模拟试卷的处理 处理好套题与类题的关系2.处理好难题与容易题的关系3.处理好新题与成题的关系4.处理好梳理知识与作题的关系三.模拟试卷的处理 我们先让学生自己分析试卷,在分析的过程中完成以下两个表格,并在此基础上写出一份简要的小结,分析存在的问题和今后努力的方向。
具体做法1、自主分析环节三.模拟试卷的处理试卷分析表一:(注:15题---20题为解答题)三.模拟试卷的处理试卷分析表二:三.模拟试卷的处理 在自愿的基础上请两位同学根据课前的分
析对自己的考试做一个简要的总结,重点谈
谈考试中的得失,学习中存在的问题及改进
的措施,教师根据情况作适当的点评。
教师进一步用数据说话.
2.统一讲评环节2.1考情分析三.模拟试卷的处理(一)总体情况分析:数据表格一三.模拟试卷的处理三.模拟试卷的处理数据表格二三.模拟试卷的处理三.模拟试卷的处理三.模拟试卷的处理数据表格三三.模拟试卷的处理三.模拟试卷的处理 在试题分析时,并不按照试题的先后顺序讲评,而是按照知识块的划分将只是相近的试题放在一起进行讲评,对重点试题进行重点讲评。现就我们区2005年高三一模数学试卷中的函数与导数内容为例,具体谈谈如何充分发挥数学模拟试卷的功效。
2.2试题分析三.模拟试卷的处理三.模拟试卷的处理(1)以导数为工具考查函数和不等式(2)以导数为载体考查数学思想方法三.模拟试卷的处理三.模拟试卷的处理三.模拟试卷的处理练习 、g(x)分别是定义在R上的奇函数、偶函数,且 上时, , 是锐角三角形的两个锐角且 ,则下列不等式正确的是( ) (A) (B) (C) (D)三.模拟试卷的处理利用导数求函数单调区间的步骤:
(1)正确求导;
(2)确定可疑极值点,并划分区间;
(3)判断各区间的单调性。三.模拟试卷的处理三.模拟试卷的处理公式出错三.模拟试卷的处理运算出错三.模拟试卷的处理三.模拟试卷的处理二.模拟试卷的处理三.模拟试卷的处理未讨论开口方向三.模拟试卷的处理三.模拟试卷的处理区间不能取并集三.模拟试卷的处理分类讨论值得注意的问题:
(1)明确分类讨论的原因;
(2)确定分类的标准;
(3)理清分类的层次;
(4)注意分类结果的整合。三.模拟试卷的处理 ① 与模拟试卷中的文科试题的比较:
已知一、试题分析二、错误分析三、同类比较三.模拟试卷的处理②与高考试题的比较:
(2004年全国A卷理科)已知已知a ,
求函数 的单调区间.
(2004年湖南理科)已知函数 ,
其中a,e为自然数对数的底数.
(I)讨论函数 的单调区间;
(II)求函数 的在区间[0,1]上的最
大值
三.模拟试卷的处理(2005年山东)三.模拟试卷的处理(2006年湖北理科)三.模拟试卷的处理三.模拟试卷的处理(2006年湖北文科)
三.模拟试卷的处理(2006年山东)
(2006年湖南)三.模拟试卷的处理(2007年安徽)
(2007年陕西)三.模拟试卷的处理四、问题深化 以此题为载体,进行条件和结论的变化,使学生在试题变化中、在矛盾斗争冲突中来调整自己的思路,达到举一反三、触类旁通的效果。三.模拟试卷的处理
例1:已知m ,研究函数
的极大值和极小值.题型一三.模拟试卷的处理题型二例2:已知m ,若函数
在 上为单调增函数,求m的取值范围.例3:已知函数 ,
若f (x)在区间(-2,-1)上是增函数,在区间
(3,4)上是减函数,求m的取值范围.三.模拟试卷的处理例4:已知a ,函数 ,
其中e是自然对数的底数.
(I) 判断f(x)在R上的单调性
(II) 是否存在a ,使得f(x)在[1,2]上的最
小值为 .题型三三.模拟试卷的处理五、问题反思 (1) 对知识掌握的反思
(2) 对数学思想方法的反思
(3) 对自己错误的反思
首先我们应该找出自己的错误,是公式出错?运算出错?分类讨论出错?还是对讨论结果的整合出错。出现错误并不可怕,可怕的是自己安慰自己,以“不小心”进行掩盖,而是要从知识上、方法上找原因,要让自己长记性。三.模拟试卷的处理Concept 第三阶段
(5月底~高考)
三.模拟试卷的处理模拟题训练 四.最后阶段的复习一、“忆”
“忆”是对已复习过的课本内容“过电影”,也就是重新回忆一遍。“忆”的内容主要是教材的知识网络、主干知识、重点和难点。回忆基础知识时切忌零散无序,而要强调知识的结构性与整体性,加强各知识点之间的联系,形成知识网络。这种回忆不仅有利于记忆,更重要的是有利于检索和应用。我们以数列的基础知识为例,边忆边写,使淡漠的或遗忘的内容再一次强化。四.最后阶段的复习 等差、等比数列知识归纳
等差数列:(一)基础知识四.最后阶段的复习(二)深化内容
1.函数思想四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习二、“看”
“看”是以阅读的方式进行复习。在最后阶段需要看的内容较多,同学们可以从以下三方面着手。四.最后阶段的复习 看看延伸或补充的内容看已经做过的题看曾经出现过的错误四.最后阶段的复习例如与函数有关的补充定理有: 四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习四.最后阶段的复习 北京市东城区教师研修中心Thank You !不足之处恳请大家批评指正研究高考试题,探索复习策略 雷晓莉联系方式:
单位:北京东城教师研修中心数学组
地址:交道口东公街9号
邮编:100009
Tel:84010991(o)
13651227381
Email:leixiaoli03@yahoo.com.cn研究高考试题,探索复习策略
同课章节目录
