第二章 平行线与相交线学案

第二章 平行线与相交线
2.1 余角与补角
学习目标：
1、经历观察、操作、推理、交流等过程，进一步发展空间观
念、推理能力和有条理表达的能力。
2、在具体情景中了解补角、余角、对顶角，知道等角的余角相等、等角的补角相等、对顶角相等，并能解决一些实际问题。
学习过程：
一、知识回顾
1、在同一平面内，两条直线有_______和_______两种位置关系.
2、角的概念 ，我们学过角的表示方法有 N
二、学习新课 A B
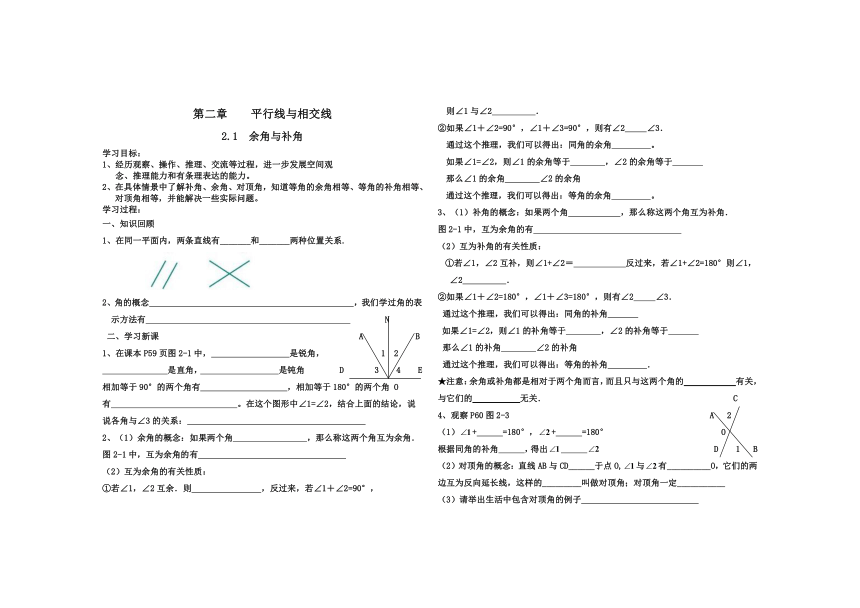
1、在课本P59页图2-1中， 是锐角， 1 2
是直角， 是钝角 D 3 4 E
相加等于90°的两个角有 ，相加等于180°的两个角 O
有 。在这个图形中∠1=∠2，结合上面的结论，说
说各角与∠3的关系：
2、（1）余角的概念：如果两个角 ，那么称这两个角互为余角．
图2-1中，互为余角的有
（2）互为余角的有关性质：
①若∠1，∠2互余．则 ，反过来，若∠1＋∠2=90°，
则∠1与∠2 ．
②如果∠1＋∠2=90°，∠1＋∠3=90°，则有∠2 ∠3．
通过这个推理，我们可以得出：同角的余角 。
如果∠1=∠2，则∠1的余角等于 ，∠2的余角等于
那么∠1的余角 ∠2的余角
通过这个推理，我们可以得出：等角的余角 。
3、（1）补角的概念：如果两个角 ，那么称这两个角互为补角．
图2-1中，互为余角的有
（2）互为补角的有关性质：
①若∠1，∠2互补，则∠1+∠2＝ 反过来，若∠1+∠2=180°则∠1，∠2 ．
②如果∠1＋∠2=180°，∠1＋∠3=180°，则有∠2 ∠3．
通过这个推理，我们可以得出：同角的补角
如果∠1=∠2，则∠1的补角等于 ，∠2的补角等于
那么∠1的补角 ∠2的补角
通过这个推理，我们可以得出：等角的补角 ．
★注意：余角或补角都是相对于两个角而言，而且只与这两个角的 有关，与它们的 无关． C
4、观察P60图2-3 A 2
（1）+ =180°，+ =180° O
根据同角的补角 ，得出 D 1 B
（2）对顶角的概念：直线AB与CD______于点O,与有__________O，它们的两边互为反向延长线，这样的_________叫做对顶角；对顶角一定___________
（3）请举出生活中包含对顶角的例子
三、巩固新知
1、已知∠α= 48°21′则∠α的余角等于________，补角等于__________
2、 一个角的补角是它的余角的3倍，则这个角为( )
A、22.5° B、50° C、45° D、135°
3、判断
(1)两直线相交，有公共顶点的角是对顶角． ( )
(2)一个钝角的补角比它的余角大90 ． ( )
(3)如果一个角等于它的补角，那么这个角一定是直角．( )
(4)相等的角一定是对顶角 ( )
(5)一个角的余角必为锐角，一个角的补角必为钝角 （ ）
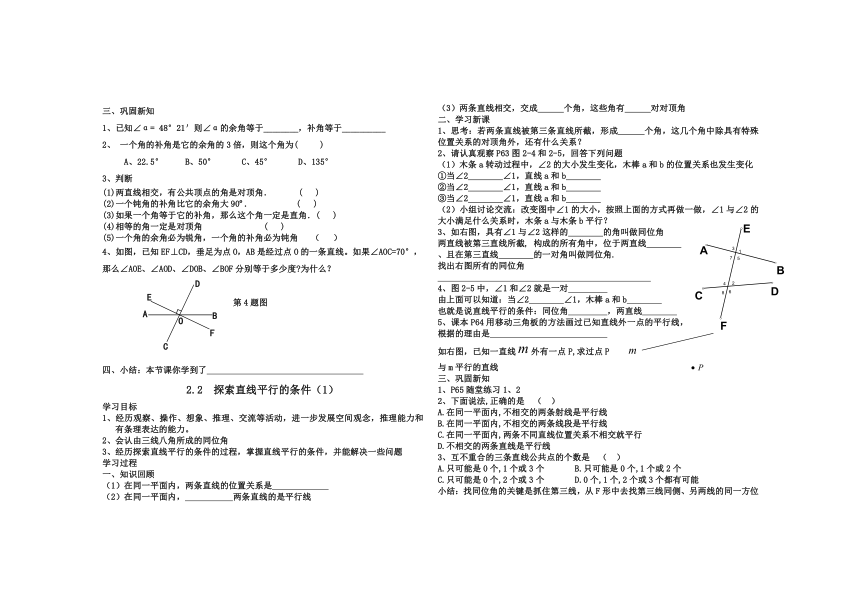
4、如图，已知EF⊥CD，垂足为点O，AB是经过点O的一条直线。如果∠AOC=70°，那么∠AOE、∠AOD、∠DOB、∠BOF分别等于多少度 为什么？
第4题图
四、小结：本节课你学到了
2.2 探索直线平行的条件（1）
学习目标
1、经历观察、操作、想象、推理、交流等活动，进一步发展空间观念，推理能力和有条理表达的能力。
2、会认由三线八角所成的同位角
3、经历探索直线平行的条件的过程，掌握直线平行的条件，并能解决一些问题
学习过程
一、知识回顾
（1）在同一平面内，两条直线的位置关系是
（2）在同一平面内， 两条直线的是平行线
（3）两条直线相交，交成 个角，这些角有 对对顶角
二、学习新课
1、思考：若两条直线被第三条直线所截，形成 个角，这几个角中除具有特殊位置关系的对顶角外，还有什么关系？
2、请认真观察P63图2-4和2-5，回答下列问题
（1）木条a转动过程中，∠2的大小发生变化，木棒a和b的位置关系也发生变化
①当∠2 ∠1，直线a和b
②当∠2 ∠1，直线a和b
③当∠2 ∠1，直线a和b
（2）小组讨论交流：改变图中∠1的大小，按照上面的方式再做一做，∠1与∠2的大小满足什么关系时，木条a与木条b平行？
3、如右图，具有∠1与∠2这样的 的角叫做同位角
两直线被第三直线所截, 构成的所有角中，位于两直线
、且在第三直线 的一对角叫做同位角.
找出右图所有的同位角
4、图2-5中，∠1和∠2就是一对
由上面可以知道：当∠2 ∠1，木棒a和b
也就是说直线平行的条件：同位角 ，两直线
5、课本P64用移动三角板的方法画过已知直线外一点的平行线，根据的理由是
如右图，已知一直线外有一点P,求过点P
与m平行的直线
三、巩固新知
1、P65随堂练习1、2
2、下面说法,正确的是　（ ）
A.在同一平面内,不相交的两条射线是平行线
B.在同一平面内,不相交的两条线段是平行线
C.在同一平面内,两条不同直线位置关系不相交就平行
D.不相交的两条直线是平行线
3、互不重合的三条直线公共点的个数是　（ ）
A.只可能是0个,1个或3个 B.只可能是0个,1个或2个
C.只可能是0个,2个或3个 D.0个,1个,2个或3个都有可能
小结：找同位角的关键是抓住第三线，从F形中去找第三线同侧、另两线的同一方位的两个角
2.1 探索直线平行的条件（2）
学习目标：
1、经历观察、操作、想象、推理、交流等活动，进一步发展空间观念、推理能力和
有条理表达的能力。
2、经历探索直线平行的条件的过程，掌握直线平行的条件，并能解决一些问题。
3、会用三角尺过已知直线外一点画这条直线的平行线。
学习过程
一、 知识回顾
1、从数量上看，两直线相交成 个角，从位置关系看，两直线相交成
对对顶角。
2、在“三线八角”中，除了能找到互为补角的角、对顶角外，还能找出
二、学习新课
1、阅读P66和观察图2-7，回答问题
（1）线段AB把小画板分成 个角，其中∠1与∠4、∠3和∠2都是互为
（2）
1 如左图，具有∠1与∠2这样位置关系的角
4 称为 ，具有∠1与∠3这样位置关系
的角称为
3 2
找出其它内错角和同旁内角
2、(1)如右图所示，两直线AB和CD被第三条直线EF所截，已知
内错角∠1=∠2，试说明直线AB//CD
理由: ∠2的对项角是 ，
所以∠2 = ∠3，（ ）
又因为 ∠1 = ∠2，（ ）
所以 ∠3 = ∠1，（ ）
所以直线 AB∥CD . （ ）
所以得出结论:内错角 ，两直线平行；
（2）如果（1）已知条件改为∠1+∠4=180°，能不能说明AB//CD
理由：因为∠2和∠4
∠1和∠4也 （ ）
所以∠1 ∠2（ ）
又因为∠1和∠2是
所以直线AB∥CD （ ）
于是得出结论：同旁内角 ，两直线平行
3、“三线八角” 小结
（1）位于两直线同一方、且在第三直线同一侧的两个角，叫做
（2）位于两直线的 ，且在第三直线的 的两个角，叫做内错角
（3）位于两直线的 ，且在第三直线的 的两个角，叫做同旁内角
4、观察图2-8，图中有 平行线，说出你的判定理由
三、巩固新知
1、P68随堂练习1、2
2、小结：（1）三线八角中，同位角 对，内错角 对，同旁内角 对
（2）证明两直线平行, 要根据已知条件, 选定同位角相等、内错角相等及同旁内角互补之一来进行
四、能力提升
1、如图(1)
（1）如果∠1=∠4，根据_________________，可得AB∥CD；
（2）如果∠1=∠2，根据_________________，可得AB∥CD；
（3）如果∠1+∠3=1800，根据______________，可得AB∥CD .
图1
2、如图(2)
（1）如果∠1=∠D，那么______∥________；
（2）如果∠1=∠B，那么______∥________；
（3）如果∠A+∠B=1800，那么______∥________；
（4）如果∠A+∠D=1800，那么______∥________；
3、在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行吗？为什么？
2.3 平行线的特征
学习目标
1、经历观察、操作、推理、交流等活动，进一步发展空间观念、推理能力和有条理表达的能力.
2、经历探索平行线的特征的过程，掌握平行线的特征，并能解决一些问题.
学习过程
一、 知识回顾
前面两节课，我们共同探讨了直线平行的条件，请写出直线平行的条件：
1、 两直线平行.
2、 两直线平行.
3、 两直线平行.
请观察上面的三个直线平行的条件的共同点是什么呢？
都是由 或 ，推出两直线平行.
那反过来，如果有两条直线平行，那么同位角、内错角、同旁内角各有什么关系呢？
二、学习新课
1、如图1，直线a与直线b平行.
图1 图2
测量同位角∠1 ∠5，图中还有其他的同位角，它们的大小也是 的。
是不是所有的同位角都相等呢？
2、如图2中的∠1与∠2是同位角，∠1 ∠2
想一想：两条直线在什么情况下，同位角才相等？
3、如图3，直线a与直线b平行.
(1)图中有 对内错角，它们的大小关系是 ，理由
(2)图中有 对同旁内角，它们的大小关系 ，理由
(3)换另一组平行线试一试，你能得到相同的结论吗？
图3
由此我们得到了平行线的特征.
两条平行直线被第三条直线所截，同位角 ，内错角 ，同旁内角 .
简记为：
两直线平行，同位角相等
两直线平行，内错角相等.
两直线平行，同旁内角互补.
4、图4，一束平行光线AB与DE射向一个水平镜面后被反射，∠1 ∠2,∠3 ∠4.
(1)可以得到∠1 ∠3，∠2 ∠4，理由
(2)反射光线BC EF，理由
三、巩固新知
1、P71随堂练习1
2、小结：
（1）本节课我们主要学行线的特征及其应用，还了解了直线平行的条件与平行线的特征的区别.
（2）平行线的特征：
两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补.
A
B
C
D
E
F
1
2 3
4
A D
B C
1
图2
3
2 4
1
F
E
D
C
B
A