1.1 平面直角坐标系 课件1(共20张PPT)
文档属性
| 名称 | 1.1 平面直角坐标系 课件1(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-20 00:00:00 | ||
图片预览








文档简介
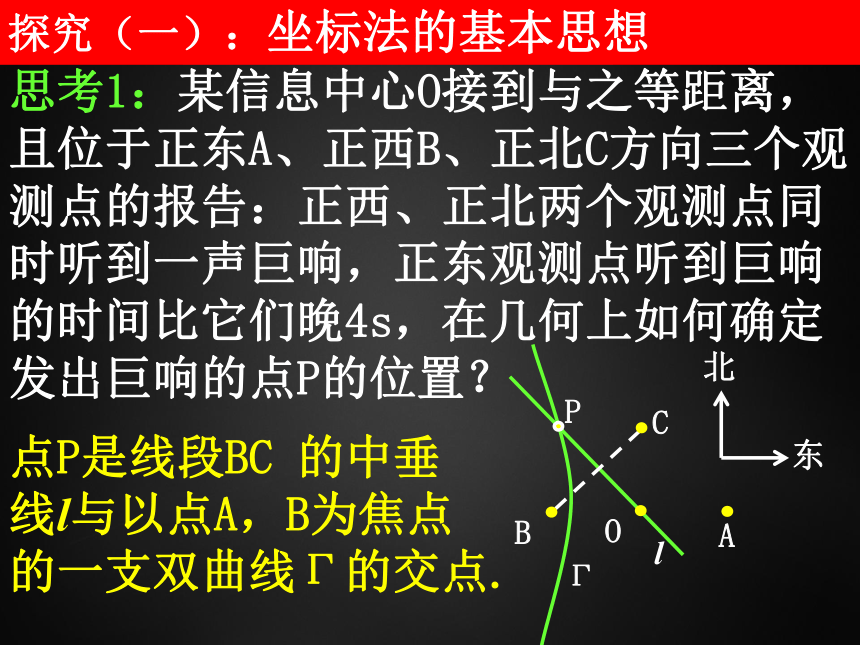
课件20张PPT。平面直角坐标系问题提出 1.平面直角坐标系是沟通几何与代数的桥梁,通过直角坐标系,使平面上的点与坐标,曲线与方程,函数与图象建立了对应关系.选择适当的直角坐标系,建立几何对象的方程,再通过方程研究它的性质及与其他几何图形的关系,这就是研究几何问题的坐标法. 2.在平面直角坐标系中,我们可以将几何图形进行平移、伸缩,经过伸缩变换后的曲线方程与原曲线方程有什么内在联系,是需要我们进一步明确的问题.探究(一):坐标法的基本思想 思考1:某信息中心O接到与之等距离,且位于正东A、正西B、正北C方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比它们晚4s,在几何上如何确定发出巨响的点P的位置? 点P是线段BC 的中垂线l与以点A,B为焦点的一支双曲线Г的交点.思考2:已知各观测点到中心O的距离都是1020m,若具体确定点P的位置,可借助直角坐标系解决,怎样建立直角坐标系才有利于运算?以信息中心O为原点,直线BA为x轴. 思考3:在上述直角坐标系中,直线l与双曲线Г的方程分别是什么? l :x+y=0 Г:思考4:点P的坐标是什么?用哪种方式指出响声点P的位置更方便?位置:西北方向距离中心 处. 思考5:一般地,用坐标法解决几何问题的基本思路是什么? 建立直角坐标系 →求曲线方程 →求相关数据 →回归原几何问题. 探究(二):平面直角坐标系中的伸缩变换 思考1:根据图象变换原理,怎样由正弦曲线y=sinx得到曲线y=sin2x?图象上各点的纵坐标不变,横坐标缩短
到原来的 倍.思考2:这是一种压缩变换,一般地,设点P(x,y)为平面直角坐标系中任意一点,保持纵坐标不变,将横坐标缩短到原来的 ,得到点P′(x′,y′),那么
x与x′,y与y′的关系如何?思考3:根据图象变换原理,怎样由正弦曲线y=sinx得到曲线y=3sinx?图象上各点的横坐标不变,纵坐标伸长到原来的3倍.思考4:这是一种伸长变换,一般地,设点P(x,y)为平面直角坐标系中任意一点,保持横坐标不变,将纵坐标伸长到原来的3倍,得到点P′(x′,y′),那么x与x′,y与y′的关系如何?思考5:根据图象变换原理,怎样由正弦曲线y=sinx得到曲线y=3sin2x?图象上各点的横坐标缩短到原来的 倍,纵坐标伸长到原来的3倍.思考6:这是一种伸缩变换,一般地,设点P(x,y)为平面直角坐标系中任意一点,将横坐标缩短到原来的 ,纵坐标伸长到原来的3倍,得到点P′(x′,y′),那么x与x′,y与y′的关系如何?思考7:一般地,设点P(x,y)为平面直角坐标系中任意一点,在变换
(λ,μ>0)的作用下,点
P(x,y)对应到点P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换,如何根据λ和μ的取值来判断所作变换是伸长变换还是压缩变换?λ和μ大于1时是伸长变换,λ和μ小于1时是压缩变换.思考8:在伸缩变换φ中,若λ,μ不同时为1,则共可产生多少种不同的伸缩变换类型? 有8种 理论迁移 例1 已知△ABC的三边a,b,c满足 b2+c2=5a2,点E,F分别为AC,AB的中点,试推断直线BE与CF的位置关系.BE⊥CF 例2 如图,圆O1和圆O2的半径都为1,圆心距为4,过两圆外的动点P分别作两圆的切线,切点分别为M,N,若|PM|= |PN|,求点P的轨迹.点P的轨迹是以点(6,0)为圆心, 为半 径的一个圆. 例3 在平面直角坐标系中,求下列
方程所对应的图形经过伸缩变换
后的图形.
(1)2x+3y=0;
(2)x2+y2=1.(1)变成直线x′+y′=0.(2)变成椭圆 . 例4 求伸缩变换φ,使得曲线 4x2+9y2=36变成曲线x′2+y′2=4. 例5 已知圆锥曲线C经过伸缩变换 后,变成曲线x′2-9y′2=9,
求曲线C的离心率.小结作业 1.建立平面直角坐标系,能将几何问题转化为代数问题来解决,这是坐标法的核心思想.在同一个问题中,直角坐标系的选取是不唯一的,但选取不同的直角坐标系对运算量有一定的影响. 2.在建立平面直角坐标系时,如果图形具有对称性,一般取对称中心为坐标原点,取对称轴为坐标轴,并尽可能使图形上的特殊点在坐标轴上,这能起到简化运算的作用. 3.有些平面图形经过伸缩变换后,可以改变原来的类型,如圆可以变成椭圆,椭圆可以变成圆;但有些平面图形经过伸缩变换后,不会改变原来的类型,如直线仍变成直线,抛物线仍变成抛物线,双曲线仍变成双曲线. 4.在伸缩变换中,变换前方程中的变量用x,y表示,变换后方程中的变量用x′,y′表示,这样可以避免新旧曲线相混淆.
到原来的 倍.思考2:这是一种压缩变换,一般地,设点P(x,y)为平面直角坐标系中任意一点,保持纵坐标不变,将横坐标缩短到原来的 ,得到点P′(x′,y′),那么
x与x′,y与y′的关系如何?思考3:根据图象变换原理,怎样由正弦曲线y=sinx得到曲线y=3sinx?图象上各点的横坐标不变,纵坐标伸长到原来的3倍.思考4:这是一种伸长变换,一般地,设点P(x,y)为平面直角坐标系中任意一点,保持横坐标不变,将纵坐标伸长到原来的3倍,得到点P′(x′,y′),那么x与x′,y与y′的关系如何?思考5:根据图象变换原理,怎样由正弦曲线y=sinx得到曲线y=3sin2x?图象上各点的横坐标缩短到原来的 倍,纵坐标伸长到原来的3倍.思考6:这是一种伸缩变换,一般地,设点P(x,y)为平面直角坐标系中任意一点,将横坐标缩短到原来的 ,纵坐标伸长到原来的3倍,得到点P′(x′,y′),那么x与x′,y与y′的关系如何?思考7:一般地,设点P(x,y)为平面直角坐标系中任意一点,在变换
(λ,μ>0)的作用下,点
P(x,y)对应到点P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换,如何根据λ和μ的取值来判断所作变换是伸长变换还是压缩变换?λ和μ大于1时是伸长变换,λ和μ小于1时是压缩变换.思考8:在伸缩变换φ中,若λ,μ不同时为1,则共可产生多少种不同的伸缩变换类型? 有8种 理论迁移 例1 已知△ABC的三边a,b,c满足 b2+c2=5a2,点E,F分别为AC,AB的中点,试推断直线BE与CF的位置关系.BE⊥CF 例2 如图,圆O1和圆O2的半径都为1,圆心距为4,过两圆外的动点P分别作两圆的切线,切点分别为M,N,若|PM|= |PN|,求点P的轨迹.点P的轨迹是以点(6,0)为圆心, 为半 径的一个圆. 例3 在平面直角坐标系中,求下列
方程所对应的图形经过伸缩变换
后的图形.
(1)2x+3y=0;
(2)x2+y2=1.(1)变成直线x′+y′=0.(2)变成椭圆 . 例4 求伸缩变换φ,使得曲线 4x2+9y2=36变成曲线x′2+y′2=4. 例5 已知圆锥曲线C经过伸缩变换 后,变成曲线x′2-9y′2=9,
求曲线C的离心率.小结作业 1.建立平面直角坐标系,能将几何问题转化为代数问题来解决,这是坐标法的核心思想.在同一个问题中,直角坐标系的选取是不唯一的,但选取不同的直角坐标系对运算量有一定的影响. 2.在建立平面直角坐标系时,如果图形具有对称性,一般取对称中心为坐标原点,取对称轴为坐标轴,并尽可能使图形上的特殊点在坐标轴上,这能起到简化运算的作用. 3.有些平面图形经过伸缩变换后,可以改变原来的类型,如圆可以变成椭圆,椭圆可以变成圆;但有些平面图形经过伸缩变换后,不会改变原来的类型,如直线仍变成直线,抛物线仍变成抛物线,双曲线仍变成双曲线. 4.在伸缩变换中,变换前方程中的变量用x,y表示,变换后方程中的变量用x′,y′表示,这样可以避免新旧曲线相混淆.
