勾股定理
图片预览



文档简介
课件17张PPT。19.1 勾 股 定 理 正方形 1中含有 个
小方格,即S1是 个单
位面积. 正方形 2的面积
是 个单位面积.正方形 3的面积是
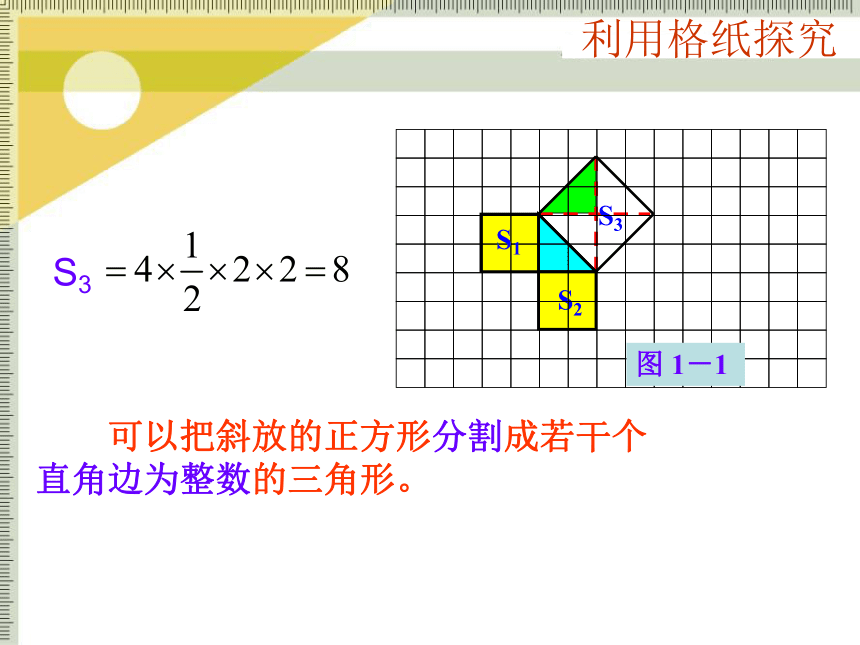
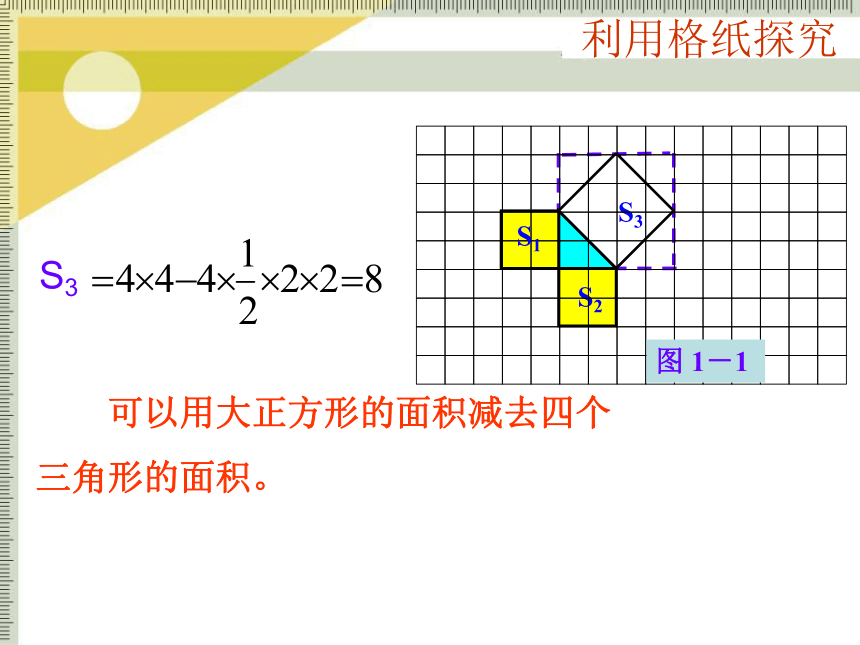
个单位面积.444正方形3的面积你是怎样得到的?S2S3图 1-1S18 1.在行距、列距都是1的方格网中,作一个以格点为顶点的直角三角形。然后,分别以三角形的各边为正方形的一边,向形外作正方形。 可以把斜放的正方形分割成若干个直角边为整数的三角形。S2S3图 1-1S1利用格纸探究S2S3图 1-1S1利用格纸探究 可以用大正方形的面积减去四个
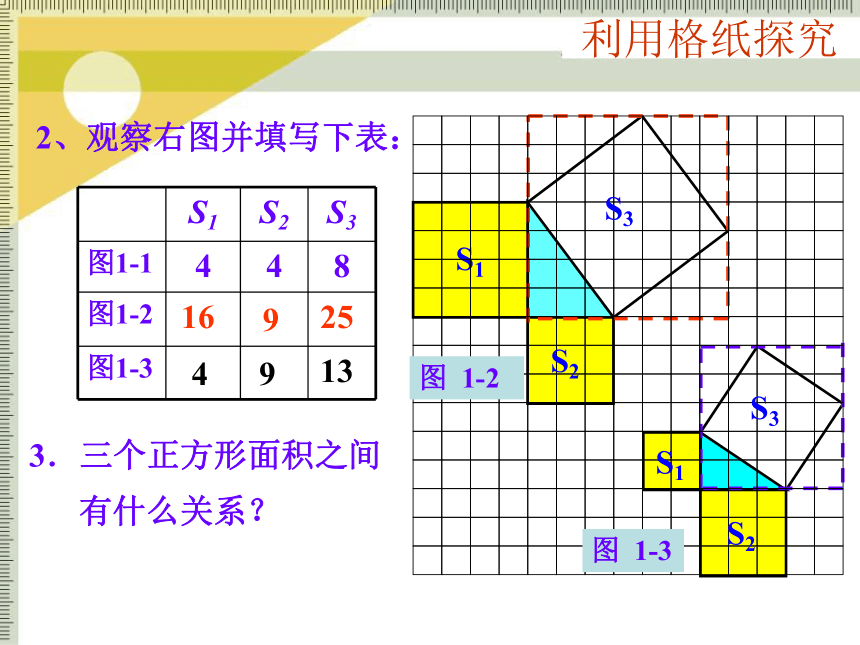
三角形的面积。S12、观察右图并填写下表:169254913S1S2S2S3S3图 1-2图 1-33.三个正方形面积之间
有什么关系?利用格纸探究3.三个正方形面积之间
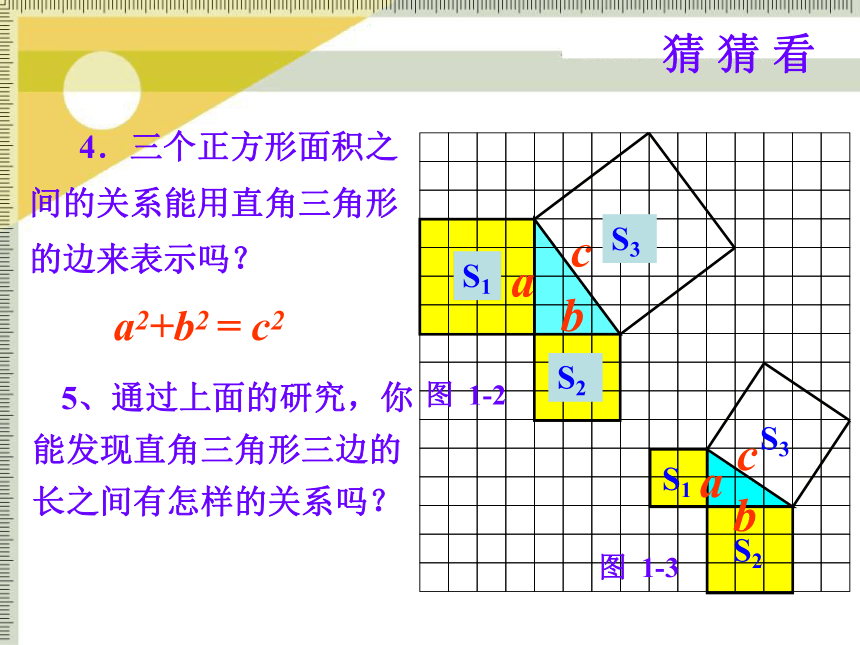
有什么关系?S1+S2=S3 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积. 4.三个正方形面积之间的关系能用直角三角形 的边来表示吗?ca2+b2 = c2abbac猜 猜 看 5、通过上面的研究,你 能发现直角三角形三边的长之间有怎样的关系吗?利用拼图来验证勾股定理:1、准备四个全等的直角三角形(设两条
直角边分别为a,b,斜边c);2、你能用这四个直角三角形拼成一个正方形吗?
拼一拼试试看3、你拼的正方形中是否含有以
斜边c为边 的正方形?4、你能否就你拼出的图说明a2+b2=c2?∵ (a+b)2 =a2+2ab+b2 = c2 +2ab∴ a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为(a+b)2=2ab+b2-2ab+a2 =a2+b2∴ a2+b2 = c2大正方形的面积可以表示为 ;
也可以表示为c2 如果直角三角形两直角边分别
为a、b, 斜边为c,那么定理 直角三角形两条直角边的平方和,
等于斜边的平方。勾股弦勾 股 定 理谈谈你对勾股定理的理解 1. 勾股定理揭示了直角三角形 之
间的关系. 2. 根据勾股定理,已知直角三角形 边
可求 边三边两第三 在△ ABC中, ∠C =90°.
⑴ 若a=3 , b=4 , 则 c=
⑵ 若b=7 , c=9 , 则 a=
⑶ 若a=40 , c=41 , 则 b= 591、 已知:在Rt △ ABC中,两直角边
AC=5 , BC=12.求斜边上的高CD的长动动脑,相信你能行!解 在Rt △ ABC中又∵ 2、 小明想知道旗杆的高度,他发现旗杆上的绳子垂到地面还多了2米,当他把绳子的下端拉开距旗杆底部8米时,发现绳子的末端刚好接触地面,求旗杆的高度动动脑,相信你能行!试 一 试谈谈你这节课的收获课后作业:
1、收集有关勾股定理的证明方法
2、习题19、1 第2、4题
小方格,即S1是 个单
位面积. 正方形 2的面积
是 个单位面积.正方形 3的面积是
个单位面积.444正方形3的面积你是怎样得到的?S2S3图 1-1S18 1.在行距、列距都是1的方格网中,作一个以格点为顶点的直角三角形。然后,分别以三角形的各边为正方形的一边,向形外作正方形。 可以把斜放的正方形分割成若干个直角边为整数的三角形。S2S3图 1-1S1利用格纸探究S2S3图 1-1S1利用格纸探究 可以用大正方形的面积减去四个
三角形的面积。S12、观察右图并填写下表:169254913S1S2S2S3S3图 1-2图 1-33.三个正方形面积之间
有什么关系?利用格纸探究3.三个正方形面积之间
有什么关系?S1+S2=S3 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积. 4.三个正方形面积之间的关系能用直角三角形 的边来表示吗?ca2+b2 = c2abbac猜 猜 看 5、通过上面的研究,你 能发现直角三角形三边的长之间有怎样的关系吗?利用拼图来验证勾股定理:1、准备四个全等的直角三角形(设两条
直角边分别为a,b,斜边c);2、你能用这四个直角三角形拼成一个正方形吗?
拼一拼试试看3、你拼的正方形中是否含有以
斜边c为边 的正方形?4、你能否就你拼出的图说明a2+b2=c2?∵ (a+b)2 =a2+2ab+b2 = c2 +2ab∴ a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为(a+b)2=2ab+b2-2ab+a2 =a2+b2∴ a2+b2 = c2大正方形的面积可以表示为 ;
也可以表示为c2 如果直角三角形两直角边分别
为a、b, 斜边为c,那么定理 直角三角形两条直角边的平方和,
等于斜边的平方。勾股弦勾 股 定 理谈谈你对勾股定理的理解 1. 勾股定理揭示了直角三角形 之
间的关系. 2. 根据勾股定理,已知直角三角形 边
可求 边三边两第三 在△ ABC中, ∠C =90°.
⑴ 若a=3 , b=4 , 则 c=
⑵ 若b=7 , c=9 , 则 a=
⑶ 若a=40 , c=41 , 则 b= 591、 已知:在Rt △ ABC中,两直角边
AC=5 , BC=12.求斜边上的高CD的长动动脑,相信你能行!解 在Rt △ ABC中又∵ 2、 小明想知道旗杆的高度,他发现旗杆上的绳子垂到地面还多了2米,当他把绳子的下端拉开距旗杆底部8米时,发现绳子的末端刚好接触地面,求旗杆的高度动动脑,相信你能行!试 一 试谈谈你这节课的收获课后作业:
1、收集有关勾股定理的证明方法
2、习题19、1 第2、4题
