2016年秋苏科版八年级上2.2轴对称的性质同步练习含答案
文档属性
| 名称 | 2016年秋苏科版八年级上2.2轴对称的性质同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-20 15:33:45 | ||
图片预览


文档简介
第二章
2.2
轴对称的性质
一.选择题(共13小题)
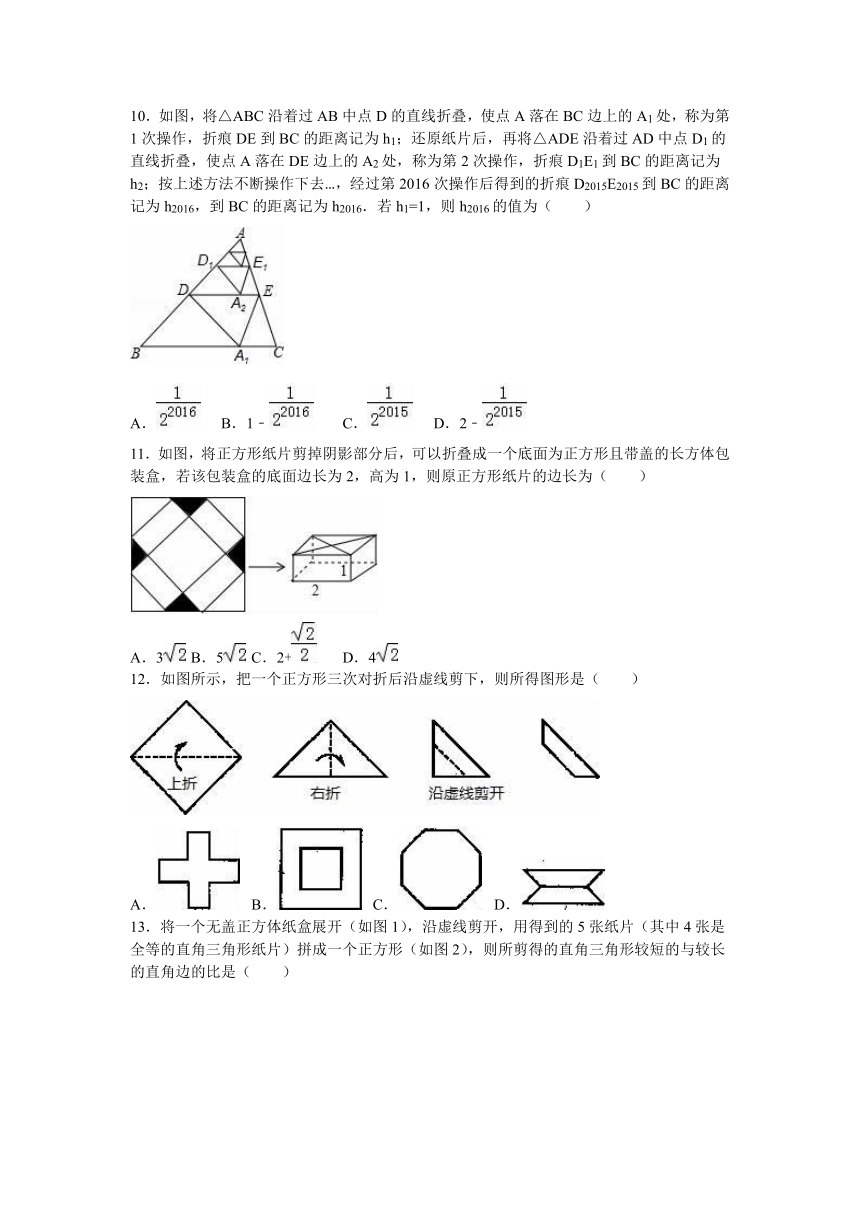
1.(2016 南充)如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
2.(2016 厦门)已知△ABC的周长是l,BC=l﹣2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
3.(2016 天津)如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
4.(2016 海南)如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
A.6
B.6
C.2
D.3
5.(2016 聊城)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
A.115°
B.120°
C.130°
D.140°
6.(2016 宿迁)如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A.2
B.
C.
D.1
7.(2016 呼伦贝尔)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为( )
A.
B.
C.4
D.5
8.下列说法中,正确的是( )
A.关于某条直线对称的两个三角形一定全等
B.两个全等三角形一定关于某条直线对称
C.面积相等的两个三角形一定关于某条直线之间对称
D.周长相等的两个三角形一定关于某条直线之间对称
9.如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时=,则△AMD′的面积与△AMN的面积的比为( )
A.1:3
B.1:4
C.1:6
D.1:9
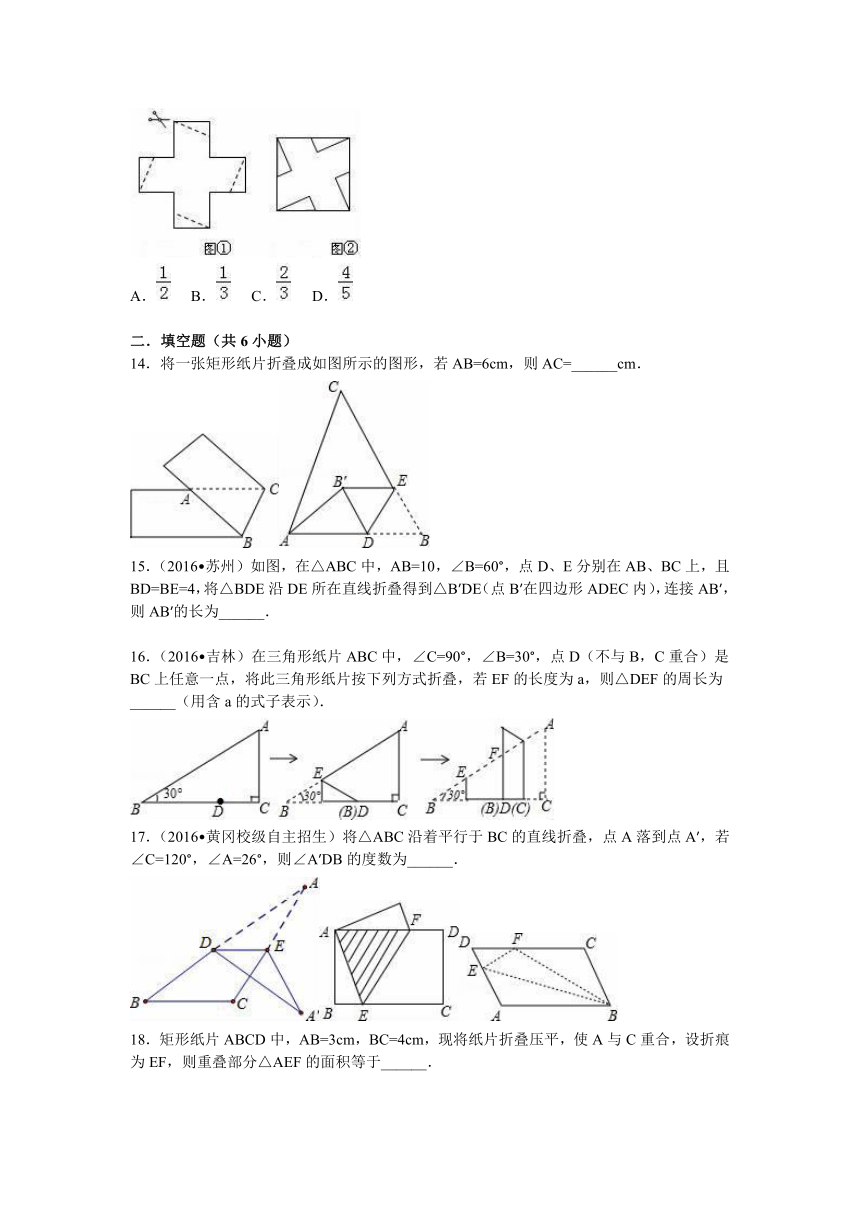
10.如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )
A.
B.1﹣
C.
D.2﹣
11.如图,将正方形纸片剪掉阴影部分后,可以折叠成一个底面为正方形且带盖的长方体包装盒,若该包装盒的底面边长为2,高为1,则原正方形纸片的边长为( )
A.3
B.5
C.2+
D.4
12.如图所示,把一个正方形三次对折后沿虚线剪下,则所得图形是( )
A.
B.
C.
D.
13.将一个无盖正方体纸盒展开(如图1),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图2),则所剪得的直角三角形较短的与较长的直角边的比是( )
A.
B.
C.
D.
二.填空题(共6小题)
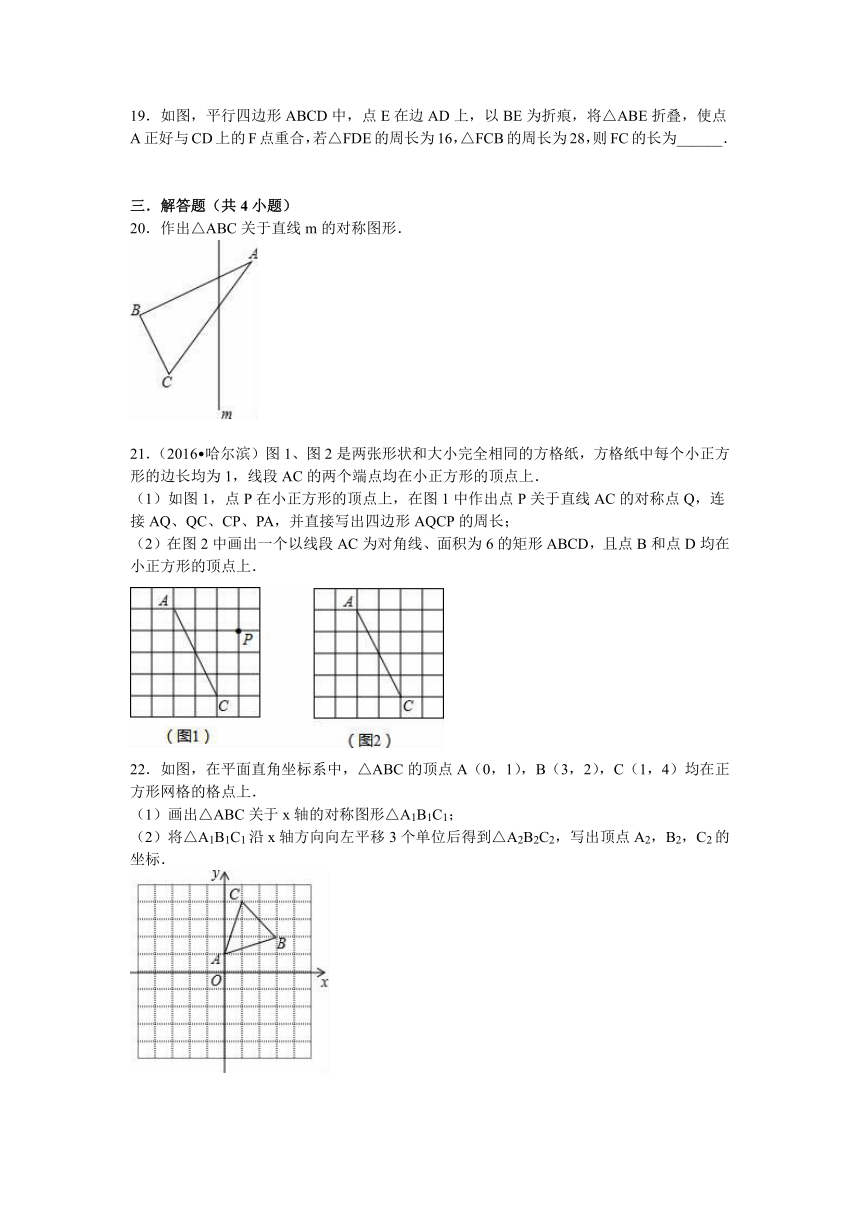
14.将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC=______cm.
15.(2016 苏州)如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为______.
16.(2016 吉林)在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为______(用含a的式子表示).
17.(2016 黄冈校级自主招生)将△ABC沿着平行于BC的直线折叠,点A落到点A′,若∠C=120°,∠A=26°,则∠A′DB的度数为______.
18.矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于______.
19.如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为______.
三.解答题(共4小题)
20.作出△ABC关于直线m的对称图形.
21.(2016 哈尔滨)图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
22.如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
23.如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2)参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
参考答案
一.选择题(共13小题)
1.(2016 南充)如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
【分析】根据直线MN是四边形AMBN的对称轴,得到点A与点B对应,根据轴对称的性质即可得到结论.
【解答】解:∵直线MN是四边形AMBN的对称轴,
∴点A与点B对应,
∴AM=BM,AN=BN,∠ANM=∠BNM,
∵点P时直线MN上的点,
∴∠MAP=∠MBP,
∴A,C,D正确,B错误,
故选B.
【点评】本题考查了轴对称的性质,熟练掌握轴对称的性质是解题的关键.
2.(2016 厦门)已知△ABC的周长是l,BC=l﹣2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
【分析】根据条件可以推出AB=AC,由此即可判断.
【解答】解:∵l=AB+BC+AC,
∴BC=l﹣2AB=AB+BC+AC﹣2AB,
∴AB=AC,
∴△ABC中BC边中线所在的直线是△ABC的对称轴,
故选C.
【点评】本题考查对称轴、三角形周长、等腰三角形的性质等知识,解题的关键是根据条件推出AB=AC,属于中考常考题型.
3.(2016 天津)如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
【分析】根据翻折变换的性质可得∠BAC=∠CAB′,根据两直线平行,内错角相等可得∠BAC=∠ACD,从而得到∠ACD=∠CAB′,然后根据等角对等边可得AE=CE,从而得解.
【解答】解:∵矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,
∴∠BAC=∠CAB′,
∵AB∥CD,
∴∠BAC=∠ACD,
∴∠ACD=∠CAB′,
∴AE=CE,
所以,结论正确的是D选项.
故选D.
【点评】本题考查了翻折变换的性质,平行线的性质,矩形的对边互相平行,等角对等边的性质,熟记各性质并准确识图是解题的关键.
4.(2016 海南)如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
A.6
B.6
C.2
D.3
【分析】根据折叠的性质判定△EDB是等腰直角三角形,然后再求BE.
【解答】解:根据折叠的性质知,CD=ED,∠CDA=∠ADE=45°,
∴∠CDE=∠BDE=90°,
∵BD=CD,BC=6,
∴BD=ED=3,
即△EDB是等腰直角三角形,
∴BE=BD=×3=3,
故选D.
【点评】本题考查了翻折变换,还考查的知识点有两个:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、等腰直角三角形的性质求解.
5.(2016 聊城)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
A.115°
B.120°
C.130°
D.140°
【分析】根据折叠的性质和矩形的性质得出∠BFE=∠EFB',∠B'=∠B=90°,根据三角形内角和定理求出∠CFB'=50°,进而解答即可.
【解答】解:∵把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,
∴∠BFE=∠EFB',∠B'=∠B=90°,
∵∠2=40°,
∴∠CFB'=50°,
∴∠1+∠EFB'﹣∠CFB'=180°,
即∠1+∠1﹣50°=180°,
解得:∠1=115°,
故选A.
【点评】本题考查了矩形的性质,折叠的性质,三角形的内角和定理的应用,能综合运用性质进行推理和计算是解此题的关键,注意:折叠后的两个图形全等.
6.(2016 宿迁)如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A.2
B.
C.
D.1
【分析】根据翻折不变性,AB=FB=2,BM=1,在Rt△BFM中,可利用勾股定理求出FM的值.
【解答】解:∵四边形ABCD为正方形,AB=2,过点B折叠纸片,使点A落在MN上的点F处,
∴FB=AB=2,BM=1,
则在Rt△BMF中,
FM=,
故选:B.
【点评】此题考查了翻折变换的性质,适时利用勾股定理是解答此类问题的关键.
7.(2016 呼伦贝尔)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为( )
A.
B.
C.4
D.5
【分析】设BQ=x,则由折叠的性质可得DQ=AQ=9﹣x,根据中点的定义可得BD=3,在Rt△BQD中,根据勾股定理可得关于x的方程,解方程即可求解.
【解答】解:设BQ=x,由折叠的性质可得DQ=AQ=9﹣x,
∵D是BC的中点,
∴BD=3,
在Rt△BQD中,x2+32=(9﹣x)2,
解得:x=4.
故线段BQ的长为4.
故选:C.
【点评】此题考查了翻折变换(折叠问题),折叠的性质,勾股定理,中点的定义以及方程思想,综合性较强.
8.下列说法中,正确的是( )
A.关于某条直线对称的两个三角形一定全等
B.两个全等三角形一定关于某条直线对称
C.面积相等的两个三角形一定关于某条直线之间对称
D.周长相等的两个三角形一定关于某条直线之间对称
【分析】认真阅读各选项提供的已知条件,根据轴对称的性质对个选项逐一验证,其中选项A是正确的.
【解答】解:A、关于某条直线对称的两个图形能够完全重合,所以关于某条直线对称的两个三角形是全等三角形,正确;
B、全等三角形不一定关于某直线对称,错误;
C、面积相等的两个三角形不一定关于某条直线之间对称,错误;
D、周长相等的两个三角形不一定关于某条直线之间对称,错误;
故选A
【点评】主要考查了轴对称的性质;找着每个选项正误的具体原因是正确解答本题的关键.
9.如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时=,则△AMD′的面积与△AMN的面积的比为( )
A.1:3
B.1:4
C.1:6
D.1:9
【分析】由=,可知,易证AN=AM,得到,于是可求出△AMD′的面积与△AMN的面积的比.
【解答】解:根据折叠的性质,AN=CN,∠ANM=∠CNM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CNM=∠AMN,
∴∠ANM=∠AMN,
∴AM=AN,
∵=,
∴,
∴,
∴△AMD′的面积:△AMN的面积=1:3.
故选:A.
【点评】本题主要考查了图形的折叠问题、等高的三角形面积比等于底的比,把△AMD′的面积与△AMN的面积的比转化为边的比,运用等高的三角形面积比等于底的比这一性质是解决问题的关键.
10.如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )
A.
B.1﹣
C.
D.2﹣
【分析】根据中点的性质及折叠的性质可得DA=DA'=DB,从而可得∠ADA'=2∠B,结合折叠的性质可得∠ADA'=2∠ADE,可得∠ADE=∠B,继而判断DE∥BC,得出DE是△ABC的中位线,证得AA1⊥BC,得到AA1=2,求出h1=2﹣1=1,同理h2=2﹣,h3=2﹣×=2﹣,于是经过第n次操作后得到的折痕Dn﹣1En﹣1到BC的距离hn=2﹣,求得结果h2016=2﹣.
【解答】解:连接AA1.
由折叠的性质可得:AA1⊥DE,DA=DA1,
又∵D是AB中点,
∴DA=DB,
∴DB=DA1,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE∥BC,
∴AA1⊥BC,
∴AA1=2,
∴h1=2﹣1=1,
同理,h2=2﹣,h3=2﹣×=2﹣
…
∴经过第n次操作后得到的折痕Dn﹣1En﹣1到BC的距离hn=2﹣.
∴h2016=2﹣.
故选:D.
【点评】本题考查了相似三角形的判定和性质,三角形中位线的性质,平行线等分线段定理,找出规律是解题的关键.
11.如图,将正方形纸片剪掉阴影部分后,可以折叠成一个底面为正方形且带盖的长方体包装盒,若该包装盒的底面边长为2,高为1,则原正方形纸片的边长为( )
A.3
B.5
C.2+
D.4
【分析】如图,由题意,△CDE,△DBF都是等腰直角三角形,分别求出CD,DB即可解决问题.
【解答】解:如图,由题意,△CDE,△DBF都是等腰直角三角形,
∵CE=DE=1,
∴CD=,∵DF=2,
∴DB=AC=,
∴AB=AC+CD+DB=3,
故选A.
【点评】本题考查翻折变换、正方形的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会看懂图形,搞清楚已知条件,属于中考常考题型.
12.如图所示,把一个正方形三次对折后沿虚线剪下,则所得图形是( )
A.
B.
C.
D.
【分析】找出题中的折叠规律,利用正方形纸片按照此方法沿虚线减下,展开即可得到剩下的图形.
【解答】解:由题意可知:减去的部分为四个等腰直角三角形的斜边构成的正方形,
又原图是正方形,所以剩下的图形为大正方形除去一个小正方形.
故选B.
【点评】本题通过折叠变换考查正多边形的有关知识,及学生的逻辑思维能力.解答此类题最好动手操作,易得出答案.
13.将一个无盖正方体纸盒展开(如图1),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图2),则所剪得的直角三角形较短的与较长的直角边的比是( )
A.
B.
C.
D.
【分析】本题考查了拼摆的问题,仔细观察图形的特点作答.
【解答】解:由图可得,所剪得的直角三角形较短的边是原正方体棱长的一半,而较长的直角边正好是原正方体的棱长,
所以所剪得的直角三角形较短的与较长的直角边的比是1:2.
故选A.
【点评】本题考查了剪纸的问题,难度不大,以不变应万变,透过现象把握本质,将问题转化为熟悉的知识去解决,同时考查了学生的动手和想象能力.
二.填空题(共6小题)
14.将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC= 6 cm.
【分析】延长原矩形的边,然后根据两直线平行,内错角相等可得∠1=∠ACB,根据翻折变换的性质可得∠1=∠ABC,从而得到∠ABC=∠ACB,再根据等角对等边可得AC=AB,从而得解.
【解答】解:如图,延长原矩形的边,
∵矩形的对边平行,
∴∠1=∠ACB,
由翻折变换的性质得,∠1=∠ABC,
∴∠ABC=∠ACB,
∴AC=AB,
∵AB=6cm,
∴AC=6cm.
故答案为:6.
【点评】本题考查了翻折变换的性质,平行线的性质,等腰三角形的判定,熟记各性质是解题的关键,难点在于作出辅助线.
15.(2016 苏州)如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为 2 .
【分析】作DF⊥B′E于点F,作B′G⊥AD于点G,首先根据有一个角为60°的等腰三角形是等边三角形判定△BDE是边长为4的等边三角形,从而根据翻折的性质得到△B′DE也是边长为4的等边三角形,从而GD=B′F=2,然后根据勾股定理得到B′G=2,然后再次利用勾股定理求得答案即可.
【解答】解:如图,作DF⊥B′E于点F,作B′G⊥AD于点G,
∵∠B=60°,BE=BD=4,
∴△BDE是边长为4的等边三角形,
∵将△BDE沿DE所在直线折叠得到△B′DE,
∴△B′DE也是边长为4的等边三角形,
∴GD=B′F=2,
∵B′D=4,
∴B′G===2,
∵AB=10,
∴AG=10﹣6=4,
∴AB′===2.
故答案为:2.
【点评】本题考查了翻折变换的性质,解题的关键是根据等边三角形的判定定理判定等边三角形,难度不大.
16.(2016 吉林)在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为 3a (用含a的式子表示).
【分析】由折叠的性质得出BE=EF=a,DE=BE,则BF=2a,由含30°角的直角三角形的性质得出DF=BF=a,即可得出△DEF的周长.
【解答】解:由折叠的性质得:B点和D点是对称关系,DE=BE,
则BE=EF=a,
∴BF=2a,
∵∠B=30°,
∴DF=BF=a,
∴△DEF的周长=DE+EF+DF=BF+DF=2a+a=3a;
故答案为:3a.
【点评】本题考查了翻折变换的性质、含30°角的直角三角形的性质、三角形周长的计算;熟练掌握翻折变换的性质,由含30°角的直角三角形的性质得出DF=a是解决问题的关键.
17.将△ABC沿着平行于BC的直线折叠,点A落到点A′,若∠C=120°,∠A=26°,则∠A′DB的度数为 112° .
【分析】利用三角形的内角和为180°求出∠B,从而根据平行线的性质可得∠ADE=∠B,再由折叠的性质得出∠ADE=∠A'DE,利用平角的知识可求出∠A′DB的度数.
【解答】解:∵∠C=120°,∠A=26°,
∴∠B=180°﹣(∠A+∠C)=34°,
又∵DE∥BC,
∴∠ADE=∠B=34°,
根据折叠的性质可得∠ADE=∠A'DE,
∴∠A'DE=∠ADE=∠B=34°,
∴∠A′DB=180°﹣∠ADE﹣∠A'DE=112°.
故答案为:112°.
【点评】本题考查折叠的性质,注意掌握折叠前后对应角相等,另外解答本题需要用到三角形的内角和定理及平行线的性质,也要注意对这些基础知识的掌握.
18.矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于 .
【分析】要求重叠部分△AEF的面积,选择AF作为底,高就等于AB的长;而由折叠可知∠AEF=∠CEF,由平行得∠CEF=∠AFE,代换后,可知AE=AF,问题转化为在Rt△ABE中求
AE.
【解答】解:设AE=x,由折叠可知,EC=x,BE=4﹣x,
在Rt△ABE中,AB2+BE2=AE2,即32+(4﹣x)2=x2,
解得:x=
由折叠可知∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF=,
∴S△AEF=×AF×AB=××3=.
故答案为:.
【点评】本题考查的是图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应角相等.
19.如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为 6 .
【分析】根据翻折不变性以及平行四边形的性质,由BF+BC+CF=28,BF=AB=DF+FC,BC=AD=ED+EF,进行等量代换即可解决.
【解答】解:∵△BEF是由△BEA翻折,
∴EA=EF,BF=BA,
∵四边形ABCD是平行四边形,
∴BC=AD=AE+DE=EF+ED,AB=BF=DC=DF+CF,
∵CF+BC+BF=28,DE+EF+DF=16
∴CF+DE+EF+DF+CF=28,
∴2CF+16=28,
∴CF=6,
故答案为6.
【点评】本题考查翻折变换、平行四边形的性质,解题的关键是利用翻折不变性解决问题,学会整体代入的数学思想,属于中考常考题型.
三.解答题(共4小题)
20.作出△ABC关于直线m的对称图形.
【分析】直接利用轴对称图形的性质得出对应点的位置,进而得出答案.
【解答】解:如图所示:△A′B′C′即为所求.
【点评】此题主要考查了作轴对称变换,根据题意得出对应点位置是解题关键.
21.(2016 哈尔滨)图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
【分析】(1)直接利用网格结合勾股定理得出符合题意的答案;
(2)直接利用网格结合矩形的性质以及勾股定理得出答案.
【解答】解:(1)如图1所示:四边形AQCP即为所求,它的周长为:4×=4;
(2)如图2所示:四边形ABCD即为所求.
【点评】此题主要考查了轴对称变换以及矩形的性质、勾股定理等知识,正确应用勾股定理是解题关键.
22.如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
【分析】(1)直接利用关于x轴对称点的性质得出各对应点位置进而得出答案;
(2)直接利用平移的性质得出各对应点位置进而得出答案.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,
点A2(﹣3,﹣1),B2(0,﹣2),C2(﹣2,﹣4).
【点评】此题主要考查了轴对称变换和平移变换,根据题意得出对应点位置是解题关键.
23.如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2)参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
【分析】(1)正方形AEGF的边长是x.则BG=EC﹣BE=x﹣2,CG=FG﹣CF=x﹣3,在直角△BGC中利用勾股定理即可得到关于x的方程,即可求解;
(2)可以证明△AEF是等边三角形,△EFG是等腰三角形,作出底边上的高,利用三角函数即可求解EG,根据△BGC的周长是:BG+GC+BC=BG+GC+BD+CD=BG+GC+BE+CF=2EG即可求解.
【解答】解:(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,
D点的对称点为E、F,延长EB、FC相交于G点,
得到四边形AEGF是正方形,
根据对称的性质可得:BE=BD=2,CF=CD=3,
设AD=x,则正方形AEGF的边长是x,
则BG=EG﹣BE=x﹣2,CG=FG﹣CF=x﹣3,
在直角△BCG中,根据勾股定理可得:(x﹣2)2+(x﹣3)2=52,
解得:x=6或﹣1(舍去).
故边长是6;
(2)作GM⊥EF于点M.
根据对称的性质可得:AE=AF=AD=4,
∠EAB=∠BAD,∠FAC=∠DAC,
又∵∠BAC=30°,
∴∠EAF=60°,
∴△AEF是等边三角形,
∴EF=AE=4,∠AEF=∠AFE=60°,
∴∠GEF=∠GFE=30°,
则EG=GF,
∴EM=EF=2,
∴EG==,
∴△BGC的周长是:BG+GC+BC=BG+GC+BD+CD=BG+GC+BE+CF=2EG=.
【点评】本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
2.2
轴对称的性质
一.选择题(共13小题)
1.(2016 南充)如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
2.(2016 厦门)已知△ABC的周长是l,BC=l﹣2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
3.(2016 天津)如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
4.(2016 海南)如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
A.6
B.6
C.2
D.3
5.(2016 聊城)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
A.115°
B.120°
C.130°
D.140°
6.(2016 宿迁)如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A.2
B.
C.
D.1
7.(2016 呼伦贝尔)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为( )
A.
B.
C.4
D.5
8.下列说法中,正确的是( )
A.关于某条直线对称的两个三角形一定全等
B.两个全等三角形一定关于某条直线对称
C.面积相等的两个三角形一定关于某条直线之间对称
D.周长相等的两个三角形一定关于某条直线之间对称
9.如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时=,则△AMD′的面积与△AMN的面积的比为( )
A.1:3
B.1:4
C.1:6
D.1:9
10.如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )
A.
B.1﹣
C.
D.2﹣
11.如图,将正方形纸片剪掉阴影部分后,可以折叠成一个底面为正方形且带盖的长方体包装盒,若该包装盒的底面边长为2,高为1,则原正方形纸片的边长为( )
A.3
B.5
C.2+
D.4
12.如图所示,把一个正方形三次对折后沿虚线剪下,则所得图形是( )
A.
B.
C.
D.
13.将一个无盖正方体纸盒展开(如图1),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图2),则所剪得的直角三角形较短的与较长的直角边的比是( )
A.
B.
C.
D.
二.填空题(共6小题)
14.将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC=______cm.
15.(2016 苏州)如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为______.
16.(2016 吉林)在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为______(用含a的式子表示).
17.(2016 黄冈校级自主招生)将△ABC沿着平行于BC的直线折叠,点A落到点A′,若∠C=120°,∠A=26°,则∠A′DB的度数为______.
18.矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于______.
19.如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为______.
三.解答题(共4小题)
20.作出△ABC关于直线m的对称图形.
21.(2016 哈尔滨)图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
22.如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
23.如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2)参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
参考答案
一.选择题(共13小题)
1.(2016 南充)如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
【分析】根据直线MN是四边形AMBN的对称轴,得到点A与点B对应,根据轴对称的性质即可得到结论.
【解答】解:∵直线MN是四边形AMBN的对称轴,
∴点A与点B对应,
∴AM=BM,AN=BN,∠ANM=∠BNM,
∵点P时直线MN上的点,
∴∠MAP=∠MBP,
∴A,C,D正确,B错误,
故选B.
【点评】本题考查了轴对称的性质,熟练掌握轴对称的性质是解题的关键.
2.(2016 厦门)已知△ABC的周长是l,BC=l﹣2AB,则下列直线一定为△ABC的对称轴的是( )
A.△ABC的边AB的垂直平分线
B.∠ACB的平分线所在的直线
C.△ABC的边BC上的中线所在的直线
D.△ABC的边AC上的高所在的直线
【分析】根据条件可以推出AB=AC,由此即可判断.
【解答】解:∵l=AB+BC+AC,
∴BC=l﹣2AB=AB+BC+AC﹣2AB,
∴AB=AC,
∴△ABC中BC边中线所在的直线是△ABC的对称轴,
故选C.
【点评】本题考查对称轴、三角形周长、等腰三角形的性质等知识,解题的关键是根据条件推出AB=AC,属于中考常考题型.
3.(2016 天津)如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′
B.∠ACD=∠B′CD
C.AD=AE
D.AE=CE
【分析】根据翻折变换的性质可得∠BAC=∠CAB′,根据两直线平行,内错角相等可得∠BAC=∠ACD,从而得到∠ACD=∠CAB′,然后根据等角对等边可得AE=CE,从而得解.
【解答】解:∵矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,
∴∠BAC=∠CAB′,
∵AB∥CD,
∴∠BAC=∠ACD,
∴∠ACD=∠CAB′,
∴AE=CE,
所以,结论正确的是D选项.
故选D.
【点评】本题考查了翻折变换的性质,平行线的性质,矩形的对边互相平行,等角对等边的性质,熟记各性质并准确识图是解题的关键.
4.(2016 海南)如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
A.6
B.6
C.2
D.3
【分析】根据折叠的性质判定△EDB是等腰直角三角形,然后再求BE.
【解答】解:根据折叠的性质知,CD=ED,∠CDA=∠ADE=45°,
∴∠CDE=∠BDE=90°,
∵BD=CD,BC=6,
∴BD=ED=3,
即△EDB是等腰直角三角形,
∴BE=BD=×3=3,
故选D.
【点评】本题考查了翻折变换,还考查的知识点有两个:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、等腰直角三角形的性质求解.
5.(2016 聊城)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )
A.115°
B.120°
C.130°
D.140°
【分析】根据折叠的性质和矩形的性质得出∠BFE=∠EFB',∠B'=∠B=90°,根据三角形内角和定理求出∠CFB'=50°,进而解答即可.
【解答】解:∵把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,
∴∠BFE=∠EFB',∠B'=∠B=90°,
∵∠2=40°,
∴∠CFB'=50°,
∴∠1+∠EFB'﹣∠CFB'=180°,
即∠1+∠1﹣50°=180°,
解得:∠1=115°,
故选A.
【点评】本题考查了矩形的性质,折叠的性质,三角形的内角和定理的应用,能综合运用性质进行推理和计算是解此题的关键,注意:折叠后的两个图形全等.
6.(2016 宿迁)如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A.2
B.
C.
D.1
【分析】根据翻折不变性,AB=FB=2,BM=1,在Rt△BFM中,可利用勾股定理求出FM的值.
【解答】解:∵四边形ABCD为正方形,AB=2,过点B折叠纸片,使点A落在MN上的点F处,
∴FB=AB=2,BM=1,
则在Rt△BMF中,
FM=,
故选:B.
【点评】此题考查了翻折变换的性质,适时利用勾股定理是解答此类问题的关键.
7.(2016 呼伦贝尔)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为( )
A.
B.
C.4
D.5
【分析】设BQ=x,则由折叠的性质可得DQ=AQ=9﹣x,根据中点的定义可得BD=3,在Rt△BQD中,根据勾股定理可得关于x的方程,解方程即可求解.
【解答】解:设BQ=x,由折叠的性质可得DQ=AQ=9﹣x,
∵D是BC的中点,
∴BD=3,
在Rt△BQD中,x2+32=(9﹣x)2,
解得:x=4.
故线段BQ的长为4.
故选:C.
【点评】此题考查了翻折变换(折叠问题),折叠的性质,勾股定理,中点的定义以及方程思想,综合性较强.
8.下列说法中,正确的是( )
A.关于某条直线对称的两个三角形一定全等
B.两个全等三角形一定关于某条直线对称
C.面积相等的两个三角形一定关于某条直线之间对称
D.周长相等的两个三角形一定关于某条直线之间对称
【分析】认真阅读各选项提供的已知条件,根据轴对称的性质对个选项逐一验证,其中选项A是正确的.
【解答】解:A、关于某条直线对称的两个图形能够完全重合,所以关于某条直线对称的两个三角形是全等三角形,正确;
B、全等三角形不一定关于某直线对称,错误;
C、面积相等的两个三角形不一定关于某条直线之间对称,错误;
D、周长相等的两个三角形不一定关于某条直线之间对称,错误;
故选A
【点评】主要考查了轴对称的性质;找着每个选项正误的具体原因是正确解答本题的关键.
9.如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合.若此时=,则△AMD′的面积与△AMN的面积的比为( )
A.1:3
B.1:4
C.1:6
D.1:9
【分析】由=,可知,易证AN=AM,得到,于是可求出△AMD′的面积与△AMN的面积的比.
【解答】解:根据折叠的性质,AN=CN,∠ANM=∠CNM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CNM=∠AMN,
∴∠ANM=∠AMN,
∴AM=AN,
∵=,
∴,
∴,
∴△AMD′的面积:△AMN的面积=1:3.
故选:A.
【点评】本题主要考查了图形的折叠问题、等高的三角形面积比等于底的比,把△AMD′的面积与△AMN的面积的比转化为边的比,运用等高的三角形面积比等于底的比这一性质是解决问题的关键.
10.如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )
A.
B.1﹣
C.
D.2﹣
【分析】根据中点的性质及折叠的性质可得DA=DA'=DB,从而可得∠ADA'=2∠B,结合折叠的性质可得∠ADA'=2∠ADE,可得∠ADE=∠B,继而判断DE∥BC,得出DE是△ABC的中位线,证得AA1⊥BC,得到AA1=2,求出h1=2﹣1=1,同理h2=2﹣,h3=2﹣×=2﹣,于是经过第n次操作后得到的折痕Dn﹣1En﹣1到BC的距离hn=2﹣,求得结果h2016=2﹣.
【解答】解:连接AA1.
由折叠的性质可得:AA1⊥DE,DA=DA1,
又∵D是AB中点,
∴DA=DB,
∴DB=DA1,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE∥BC,
∴AA1⊥BC,
∴AA1=2,
∴h1=2﹣1=1,
同理,h2=2﹣,h3=2﹣×=2﹣
…
∴经过第n次操作后得到的折痕Dn﹣1En﹣1到BC的距离hn=2﹣.
∴h2016=2﹣.
故选:D.
【点评】本题考查了相似三角形的判定和性质,三角形中位线的性质,平行线等分线段定理,找出规律是解题的关键.
11.如图,将正方形纸片剪掉阴影部分后,可以折叠成一个底面为正方形且带盖的长方体包装盒,若该包装盒的底面边长为2,高为1,则原正方形纸片的边长为( )
A.3
B.5
C.2+
D.4
【分析】如图,由题意,△CDE,△DBF都是等腰直角三角形,分别求出CD,DB即可解决问题.
【解答】解:如图,由题意,△CDE,△DBF都是等腰直角三角形,
∵CE=DE=1,
∴CD=,∵DF=2,
∴DB=AC=,
∴AB=AC+CD+DB=3,
故选A.
【点评】本题考查翻折变换、正方形的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会看懂图形,搞清楚已知条件,属于中考常考题型.
12.如图所示,把一个正方形三次对折后沿虚线剪下,则所得图形是( )
A.
B.
C.
D.
【分析】找出题中的折叠规律,利用正方形纸片按照此方法沿虚线减下,展开即可得到剩下的图形.
【解答】解:由题意可知:减去的部分为四个等腰直角三角形的斜边构成的正方形,
又原图是正方形,所以剩下的图形为大正方形除去一个小正方形.
故选B.
【点评】本题通过折叠变换考查正多边形的有关知识,及学生的逻辑思维能力.解答此类题最好动手操作,易得出答案.
13.将一个无盖正方体纸盒展开(如图1),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图2),则所剪得的直角三角形较短的与较长的直角边的比是( )
A.
B.
C.
D.
【分析】本题考查了拼摆的问题,仔细观察图形的特点作答.
【解答】解:由图可得,所剪得的直角三角形较短的边是原正方体棱长的一半,而较长的直角边正好是原正方体的棱长,
所以所剪得的直角三角形较短的与较长的直角边的比是1:2.
故选A.
【点评】本题考查了剪纸的问题,难度不大,以不变应万变,透过现象把握本质,将问题转化为熟悉的知识去解决,同时考查了学生的动手和想象能力.
二.填空题(共6小题)
14.将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC= 6 cm.
【分析】延长原矩形的边,然后根据两直线平行,内错角相等可得∠1=∠ACB,根据翻折变换的性质可得∠1=∠ABC,从而得到∠ABC=∠ACB,再根据等角对等边可得AC=AB,从而得解.
【解答】解:如图,延长原矩形的边,
∵矩形的对边平行,
∴∠1=∠ACB,
由翻折变换的性质得,∠1=∠ABC,
∴∠ABC=∠ACB,
∴AC=AB,
∵AB=6cm,
∴AC=6cm.
故答案为:6.
【点评】本题考查了翻折变换的性质,平行线的性质,等腰三角形的判定,熟记各性质是解题的关键,难点在于作出辅助线.
15.(2016 苏州)如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为 2 .
【分析】作DF⊥B′E于点F,作B′G⊥AD于点G,首先根据有一个角为60°的等腰三角形是等边三角形判定△BDE是边长为4的等边三角形,从而根据翻折的性质得到△B′DE也是边长为4的等边三角形,从而GD=B′F=2,然后根据勾股定理得到B′G=2,然后再次利用勾股定理求得答案即可.
【解答】解:如图,作DF⊥B′E于点F,作B′G⊥AD于点G,
∵∠B=60°,BE=BD=4,
∴△BDE是边长为4的等边三角形,
∵将△BDE沿DE所在直线折叠得到△B′DE,
∴△B′DE也是边长为4的等边三角形,
∴GD=B′F=2,
∵B′D=4,
∴B′G===2,
∵AB=10,
∴AG=10﹣6=4,
∴AB′===2.
故答案为:2.
【点评】本题考查了翻折变换的性质,解题的关键是根据等边三角形的判定定理判定等边三角形,难度不大.
16.(2016 吉林)在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为 3a (用含a的式子表示).
【分析】由折叠的性质得出BE=EF=a,DE=BE,则BF=2a,由含30°角的直角三角形的性质得出DF=BF=a,即可得出△DEF的周长.
【解答】解:由折叠的性质得:B点和D点是对称关系,DE=BE,
则BE=EF=a,
∴BF=2a,
∵∠B=30°,
∴DF=BF=a,
∴△DEF的周长=DE+EF+DF=BF+DF=2a+a=3a;
故答案为:3a.
【点评】本题考查了翻折变换的性质、含30°角的直角三角形的性质、三角形周长的计算;熟练掌握翻折变换的性质,由含30°角的直角三角形的性质得出DF=a是解决问题的关键.
17.将△ABC沿着平行于BC的直线折叠,点A落到点A′,若∠C=120°,∠A=26°,则∠A′DB的度数为 112° .
【分析】利用三角形的内角和为180°求出∠B,从而根据平行线的性质可得∠ADE=∠B,再由折叠的性质得出∠ADE=∠A'DE,利用平角的知识可求出∠A′DB的度数.
【解答】解:∵∠C=120°,∠A=26°,
∴∠B=180°﹣(∠A+∠C)=34°,
又∵DE∥BC,
∴∠ADE=∠B=34°,
根据折叠的性质可得∠ADE=∠A'DE,
∴∠A'DE=∠ADE=∠B=34°,
∴∠A′DB=180°﹣∠ADE﹣∠A'DE=112°.
故答案为:112°.
【点评】本题考查折叠的性质,注意掌握折叠前后对应角相等,另外解答本题需要用到三角形的内角和定理及平行线的性质,也要注意对这些基础知识的掌握.
18.矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于 .
【分析】要求重叠部分△AEF的面积,选择AF作为底,高就等于AB的长;而由折叠可知∠AEF=∠CEF,由平行得∠CEF=∠AFE,代换后,可知AE=AF,问题转化为在Rt△ABE中求
AE.
【解答】解:设AE=x,由折叠可知,EC=x,BE=4﹣x,
在Rt△ABE中,AB2+BE2=AE2,即32+(4﹣x)2=x2,
解得:x=
由折叠可知∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,即AE=AF=,
∴S△AEF=×AF×AB=××3=.
故答案为:.
【点评】本题考查的是图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应角相等.
19.如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为 6 .
【分析】根据翻折不变性以及平行四边形的性质,由BF+BC+CF=28,BF=AB=DF+FC,BC=AD=ED+EF,进行等量代换即可解决.
【解答】解:∵△BEF是由△BEA翻折,
∴EA=EF,BF=BA,
∵四边形ABCD是平行四边形,
∴BC=AD=AE+DE=EF+ED,AB=BF=DC=DF+CF,
∵CF+BC+BF=28,DE+EF+DF=16
∴CF+DE+EF+DF+CF=28,
∴2CF+16=28,
∴CF=6,
故答案为6.
【点评】本题考查翻折变换、平行四边形的性质,解题的关键是利用翻折不变性解决问题,学会整体代入的数学思想,属于中考常考题型.
三.解答题(共4小题)
20.作出△ABC关于直线m的对称图形.
【分析】直接利用轴对称图形的性质得出对应点的位置,进而得出答案.
【解答】解:如图所示:△A′B′C′即为所求.
【点评】此题主要考查了作轴对称变换,根据题意得出对应点位置是解题关键.
21.(2016 哈尔滨)图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
【分析】(1)直接利用网格结合勾股定理得出符合题意的答案;
(2)直接利用网格结合矩形的性质以及勾股定理得出答案.
【解答】解:(1)如图1所示:四边形AQCP即为所求,它的周长为:4×=4;
(2)如图2所示:四边形ABCD即为所求.
【点评】此题主要考查了轴对称变换以及矩形的性质、勾股定理等知识,正确应用勾股定理是解题关键.
22.如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
【分析】(1)直接利用关于x轴对称点的性质得出各对应点位置进而得出答案;
(2)直接利用平移的性质得出各对应点位置进而得出答案.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,
点A2(﹣3,﹣1),B2(0,﹣2),C2(﹣2,﹣4).
【点评】此题主要考查了轴对称变换和平移变换,根据题意得出对应点位置是解题关键.
23.如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2)参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
【分析】(1)正方形AEGF的边长是x.则BG=EC﹣BE=x﹣2,CG=FG﹣CF=x﹣3,在直角△BGC中利用勾股定理即可得到关于x的方程,即可求解;
(2)可以证明△AEF是等边三角形,△EFG是等腰三角形,作出底边上的高,利用三角函数即可求解EG,根据△BGC的周长是:BG+GC+BC=BG+GC+BD+CD=BG+GC+BE+CF=2EG即可求解.
【解答】解:(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,
D点的对称点为E、F,延长EB、FC相交于G点,
得到四边形AEGF是正方形,
根据对称的性质可得:BE=BD=2,CF=CD=3,
设AD=x,则正方形AEGF的边长是x,
则BG=EG﹣BE=x﹣2,CG=FG﹣CF=x﹣3,
在直角△BCG中,根据勾股定理可得:(x﹣2)2+(x﹣3)2=52,
解得:x=6或﹣1(舍去).
故边长是6;
(2)作GM⊥EF于点M.
根据对称的性质可得:AE=AF=AD=4,
∠EAB=∠BAD,∠FAC=∠DAC,
又∵∠BAC=30°,
∴∠EAF=60°,
∴△AEF是等边三角形,
∴EF=AE=4,∠AEF=∠AFE=60°,
∴∠GEF=∠GFE=30°,
则EG=GF,
∴EM=EF=2,
∴EG==,
∴△BGC的周长是:BG+GC+BC=BG+GC+BD+CD=BG+GC+BE+CF=2EG=.
【点评】本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
