2016年苏科版八年级上2.1轴对称与轴对称图形同步练习含答案
文档属性
| 名称 | 2016年苏科版八年级上2.1轴对称与轴对称图形同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 228.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-20 15:35:38 | ||
图片预览




文档简介
2.1
轴对称与轴对称图形
一.选择题(共8小题)
1.(2016 邵阳)下面四个手机应用图标中是轴对称图形的是( )
A.
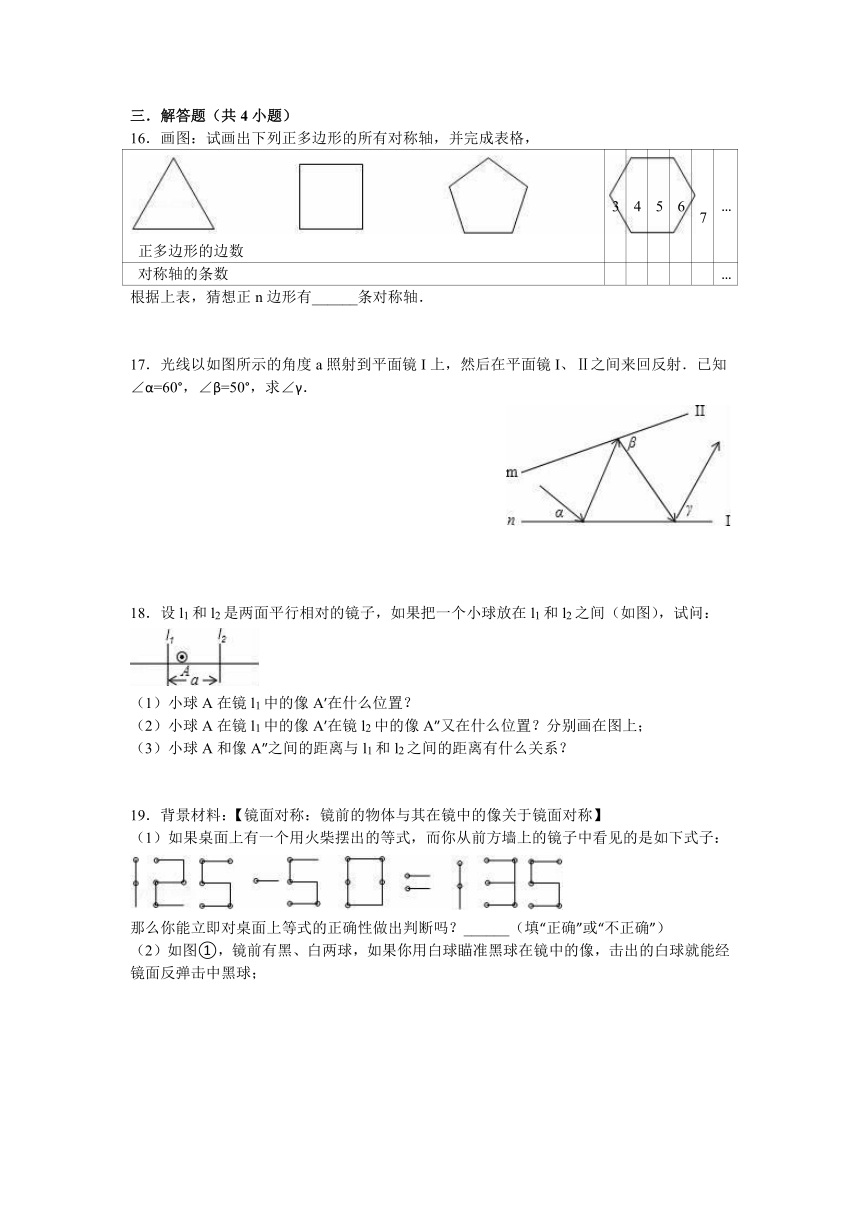
B.
C.
D.
2.(2016 西宁)在一些汉字的美术字中,有的是轴对称图形.下面四个美术字中可以看作轴对称图形的是( )
A.
B.
C.
D.
3.(2016 梧州)下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( )
A.
B.
C.
D.
4.(2016 台湾)若下列选项中的图形均为正多边形,则哪一个图形恰有4条对称轴?( )
A.
B.
C.
D.
5.(2016 诸城市一模)倡导节约,进入绿色,节约型社会,在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志,在这些标志中,是轴对称图形的是( )
A.
B.
C.
D.
6.窗花是我国传统民间艺术,下列窗花中,是轴对称图形的为( )
A.
B.
C.
D.
7.下列图形中,轴对称图形的个数是( )
A.1个
B.2个
C.3个
D.4个
8.平行四边形,矩形,菱形,等边三角形,正方形中是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共7小题)
9.(2016 赤峰)下列图表是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是______(填序号)
10.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有______种.
11.如果一个三角形是轴对称图形,且有一个角为60°,那么这个三角形是______,它有______条对称轴.
12.室内墙壁上挂一平面镜,明敏在平面镜内看到他背后墙上的时钟如图,则这时的实际时间是______.
13.如图是一个风筝的图案,它是轴对称图形,EF是对称轴.∠A=90°,∠AED=130°,∠C=45°,则∠BFC的度数为______.
14.如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为______°.
15.如图,石头A和石头B相距80cm,且关于竹竿l对称,一只电动青蛙在距竹竿30cm,距石头A为60cm的P1处,按如图所示的顺序循环跳跃.青蛙跳跃25次后停下,此时它与石头A相距______cm,与竹竿l相距______cm.
三.解答题(共4小题)
16.画图:试画出下列正多边形的所有对称轴,并完成表格,
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有______条对称轴.
17.光线以如图所示的角度a照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射.已知∠α=60°,∠β=50°,求∠γ.
18.设l1和l2是两面平行相对的镜子,如果把一个小球放在l1和l2之间(如图),试问:
(1)小球A在镜l1中的像A′在什么位置?
(2)小球A在镜l1中的像A′在镜l2中的像A″又在什么位置?分别画在图上;
(3)小球A和像A″之间的距离与l1和l2之间的距离有什么关系?
19.背景材料:【镜面对称:镜前的物体与其在镜中的像关于镜面对称】
(1)如果桌面上有一个用火柴摆出的等式,而你从前方墙上的镜子中看见的是如下式子:
那么你能立即对桌面上等式的正确性做出判断吗?______(填“正确”或“不正确”)
(2)如图①,镜前有黑、白两球,如果你用白球瞄准黑球在镜中的像,击出的白球就能经镜面反弹击中黑球;
如果你有两面互相垂直的镜子如图②,你想让击出的白球先后经两个镜面反弹,然后仍能击中黑球,那么你应该怎样瞄准?请仿照图①用箭头画出白球的运动的路线图;
(3)请利用轴对称知识解决下面问题:如图③,∠ABC=45°,D是射线BC上一点,BD=2cm,且E是BD的中点,点P是AB上一动点,求PE+PD的最小值.
参考答案
一.选择题(共8小题)
1.(2016 邵阳)下面四个手机应用图标中是轴对称图形的是( )
A.
B.
C.
D.
【分析】分别根据轴对称图形与中心对称图形的性质对各选项进行逐一分析即可.
【解答】解:A、既不是轴对称图形,也不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项错误;
C、既不是轴对称图形,也不是中心对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选D.
【点评】本题考查的是轴对称图形,熟知轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合是解答此题的关键.
2.(2016 西宁)在一些汉字的美术字中,有的是轴对称图形.下面四个美术字中可以看作轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可.
【解答】解:四个汉字中只有“善”字可以看作轴对称图形,
故选D.
【点评】考查了轴对称图形的知识,掌握轴对称图形的意义,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合.
3.(2016 梧州)下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解.
【解答】解:A、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
故选:B.
【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
4.(2016 台湾)若下列选项中的图形均为正多边形,则哪一个图形恰有4条对称轴?( )
A.
B.
C.
D.
【分析】直接利用轴对称图形的性质分析得出符合题意的答案.
【解答】解:A、正三角形有3条对称轴,故此选项错误;
B、正方形有4条对称轴,故此选项正确;
C、正六边形有6条对称轴,故此选项错误;
D、正八边形有8条对称轴,故此选项错误.
故选:B.
【点评】此题主要考查了轴对称图形,正确把握轴对称图形的定义是解题关键.
5.倡导节约,进入绿色,节约型社会,在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志,在这些标志中,是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念对各图形判断后即可得解.
【解答】解:A、不是轴对称图形,故此选项错误;
B、不是轴对称图形,故此选项错误;
C、是轴对称图形,故此选项正确;
D、不是轴对称图形,故此选项错误;
故选:C.
【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,本题仔细观察图形是解题的关键.
6.窗花是我国传统民间艺术,下列窗花中,是轴对称图形的为( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.结合选项解答即可.
【解答】解:A、不是轴对称图形,故该选项错误;
B、是轴对称图形,故该选项正确;
C、不是轴对称图形,故该选项错误;
D、不是轴对称图形,故该选项错误.
故选B.
【点评】本题考查了轴对称图形的知识,解答本题的关键是掌握轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
7.下列图形中,轴对称图形的个数是( )
A.1个
B.2个
C.3个
D.4个
【分析】根据轴对称图形的概念求解.
【解答】解:第一个图形是轴对称图形;
第二个图形是轴对称图形;
第三个图形不是轴对称图形;
第四个图形是轴对称图形;
综上共有3个轴对称图形.
故选C.
【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
8.平行四边形,矩形,菱形,等边三角形,正方形中是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据轴对称图形的概念判断求解即可.
【解答】解:矩形、菱形、等边三角形、正方形都是轴对称图形,
所以共有4个图形是轴对称图形.
故选D.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
二.填空题(共7小题)
9.(2016 赤峰)下列图表是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 ①②③④ (填序号)
【分析】结合图象根据轴对称图形的概念解答即可.
【解答】解:根据轴对称图形的概念,可得出①②③④均为轴对称图形.
故答案为:①②③④.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
10.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有 4 种.
【分析】结合图象根据轴对称图形的概念求解即可.
【解答】解:根据轴对称图形的概念可知,一共有四种涂法,如下图所示:
.
故答案为:4.
【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
11.如果一个三角形是轴对称图形,且有一个角为60°,那么这个三角形是 等边三角形 ,它有 3 条对称轴.
【分析】先由该三角形是轴对称图形,可知该三角形是等腰三角形,再根据有一个内角是60°的等腰三角形是等边三角形,解答即可.
【解答】解:∵该三角形是轴对称图形,
∴该三角形是等腰三角形,
又∵该三角形有一个角为60°,
∴这个三角形是等边三角形,
∴这个三角形有3条对称轴.
故答案为:等边三角形,3.
【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
12.室内墙壁上挂一平面镜,明敏在平面镜内看到他背后墙上的时钟如图,则这时的实际时间是 3:40 .
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
【解答】解:根据镜面对称的性质,分析可得题中所显示的时刻与3:40成轴对称,所以此时实际时刻为:3:40.
故答案为:3:40.
【点评】本题考查了镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
13.如图是一个风筝的图案,它是轴对称图形,EF是对称轴.∠A=90°,∠AED=130°,∠C=45°,则∠BFC的度数为 140° .
【分析】利用轴对称图形的性质结合四边形内角和定理得出答案.
【解答】解:∵一个风筝的图案,它是轴对称图形,EF是对称轴.∠A=90°,∠AED=130°,∠C=45°,
∴∠D=90°,∠MED=65°,
∴∠DEF=115°,
∴∠CFN=360°﹣115°﹣90°﹣45°=110°
∴∠BFC的度数为:2(180°﹣110°)=140°.
故答案为:140°.
【点评】此题主要考查了轴对称图形的性质以及四边形内角和定理,熟练应用轴对称图形的性质是解题关键.
14.如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为 60 °.
【分析】要使白球反弹后能将黑球直接撞入袋中,则∠2=60°,根据∠1、∠2对称,则能求出∠1的度数.
【解答】解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=∠2=60°.
故答案是:60.
【点评】本题考查了同学们利用对称的性质解决问题的能力,根据入射角等于反射角得到∠1=∠2是解题的难点.
15.如图,石头A和石头B相距80cm,且关于竹竿l对称,一只电动青蛙在距竹竿30cm,距石头A为60cm的P1处,按如图所示的顺序循环跳跃.青蛙跳跃25次后停下,此时它与石头A相距 60 cm,与竹竿l相距 50 cm.
【分析】先根据对称的定义即可画出图形,找到25次后的位置P2,然后根据对称定义和梯形中位线定义求解距离.
【解答】
解:青蛙跳跃25次后停下,停在P2处,P2A=P1A=60cm,
∵点B是P3P4的中点,点A是P2P1的中点,
∴AB是梯形P1P2P3P4的中位线,
∴P2P3+P1P4=2AB,即(P2P3+P1P4)÷2=80,(P2P3+60)÷2=80,
解得:P2P3=100.P2与竹竿l相距100÷2=50cm.
故答案为:60、50.
【点评】本题考查了轴对称的性质及梯形的中位线定理,解答此题要明确在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等,另外要判断出AB是梯形P1P2P3P4的中位线.
三.解答题(共4小题)
16.画图:试画出下列正多边形的所有对称轴,并完成表格,
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有 n 条对称轴.
【分析】轴对称就是一个图形的一部分,沿着一条直线对折,能够和另一部分重合,这样的图形就是轴对称图形,这条直线就是对称轴,依据定义即可求解.
【解答】解:如图,
故填3,4,5,6,7,n.
【点评】正确理解轴对称图形的定义是解决本题的关键,本题是一个基础题.
17.光线以如图所示的角度a照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射.已知∠α=60°,∠β=50°,求∠γ.
【分析】利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角和角之间的相互转换来求解.
【解答】解:如答图所示,过A作MA⊥AC,垂足为A,
则∠1=90°﹣α=90°﹣60°=30°,
∴∠2=∠1=30°,
∴∠7=90°﹣30°=60°,
过B作BN⊥m,垂足为B,
∴∠3=90°﹣β=90°﹣50°=40°,
∴∠ABC=∠3+∠4=2∠3=2×40°=80°,
过C作CE⊥AC,垂足为C,
则∠5=∠6,∠BCD=2∠5+Y=∠7+∠ABC=60°+80°=140°,
∵∠5+Y=90°,
∴∠6=∠5=50°,
∴∠Y=90°﹣50°=40°.
【点评】本题考查镜面反射的原理与性质.需注意利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角,利用平行的性质把相应的角转移到一个三角形中求解.
18.设l1和l2是两面平行相对的镜子,如果把一个小球放在l1和l2之间(如图),试问:
(1)小球A在镜l1中的像A′在什么位置?
(2)小球A在镜l1中的像A′在镜l2中的像A″又在什么位置?分别画在图上;
(3)小球A和像A″之间的距离与l1和l2之间的距离有什么关系?
【分析】(1)A′应在和A关于L1对称的位置;
(2)A″应在和A′关于L2对称的位置;
(3)由对应点到对称轴的距离相等可得A和像A″之间的距离与l1和l2之间的距离的关系.
【解答】解:(1)∵A和A′关于L1对称,
∴A′应在L1的左边,到L1的距离等于A到L1的距离;
(2)A″应在和A′关于L2对称的位置,如图;
(3)∵A和A′关于L1对称,A′和A″关于L2对称,
∴AA′=2A′C,A′A″=2A′D,
∴AA″=A′A″﹣AA′=2(A′D﹣A′C)=2a.
【点评】考查镜面对称的知识;镜面对称是轴对称的一种特殊形式,关于镜面对称的两个物体到对称轴的距离相等.
19.背景材料:【镜面对称:镜前的物体与其在镜中的像关于镜面对称】
(1)如果桌面上有一个用火柴摆出的等式,而你从前方墙上的镜子中看见的是如下式子:
那么你能立即对桌面上等式的正确性做出判断吗? 正确 (填“正确”或“不正确”)
(2)如图①,镜前有黑、白两球,如果你用白球瞄准黑球在镜中的像,击出的白球就能经镜面反弹击中黑球;
如果你有两面互相垂直的镜子如图②,你想让击出的白球先后经两个镜面反弹,然后仍能击中黑球,那么你应该怎样瞄准?请仿照图①用箭头画出白球的运动的路线图;
(3)请利用轴对称知识解决下面问题:如图③,∠ABC=45°,D是射线BC上一点,BD=2cm,且E是BD的中点,点P是AB上一动点,求PE+PD的最小值.
【分析】(1)根据镜面对称原理即可判断答案;
(2)根据镜面对称就是轴对称关于镜面对称,把物体沿对称轴旋转180°推出即可;
(3)作D点关于AB的对称点D′点,连接D′E交AB于点P,此时PE+PD最小,利用勾股定理求得D′E的长即可.
【解答】解:(1)正确,
桌面上算式是152﹣20=132,
故答案为:正确.
(2)如图(2)所示:作白球A关于镜面ON的对称点C,作黑球B关于镜面OM的对称点D,连接CD交ON于E,交OM于F,连接AE、BF,
延AE﹣EF﹣FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球,
答:延AE﹣EF﹣FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球.
;
(3)如图(3),作D点关于AB的对称点D′点,连接D′E交AB于点P,
,此时PE+PD最小,
∵D点关于AC的对称点D′点,
∴BD=D′B,
∵BD=2cm,E是BD的中点,
∴D′B=2cm,EB=1cm,
∴D′E===,
∴PE+PD的最小值为.
【点评】本题主要考查对勾股定理,正方形的性质,轴对称的性质,线段垂直平分线的性质,镜面对称,轴对称﹣最短路线问题等知识点的理解和掌握,综合运用这些性质进行画图和推理是解此题的关键.
轴对称与轴对称图形
一.选择题(共8小题)
1.(2016 邵阳)下面四个手机应用图标中是轴对称图形的是( )
A.
B.
C.
D.
2.(2016 西宁)在一些汉字的美术字中,有的是轴对称图形.下面四个美术字中可以看作轴对称图形的是( )
A.
B.
C.
D.
3.(2016 梧州)下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( )
A.
B.
C.
D.
4.(2016 台湾)若下列选项中的图形均为正多边形,则哪一个图形恰有4条对称轴?( )
A.
B.
C.
D.
5.(2016 诸城市一模)倡导节约,进入绿色,节约型社会,在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志,在这些标志中,是轴对称图形的是( )
A.
B.
C.
D.
6.窗花是我国传统民间艺术,下列窗花中,是轴对称图形的为( )
A.
B.
C.
D.
7.下列图形中,轴对称图形的个数是( )
A.1个
B.2个
C.3个
D.4个
8.平行四边形,矩形,菱形,等边三角形,正方形中是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共7小题)
9.(2016 赤峰)下列图表是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是______(填序号)
10.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有______种.
11.如果一个三角形是轴对称图形,且有一个角为60°,那么这个三角形是______,它有______条对称轴.
12.室内墙壁上挂一平面镜,明敏在平面镜内看到他背后墙上的时钟如图,则这时的实际时间是______.
13.如图是一个风筝的图案,它是轴对称图形,EF是对称轴.∠A=90°,∠AED=130°,∠C=45°,则∠BFC的度数为______.
14.如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为______°.
15.如图,石头A和石头B相距80cm,且关于竹竿l对称,一只电动青蛙在距竹竿30cm,距石头A为60cm的P1处,按如图所示的顺序循环跳跃.青蛙跳跃25次后停下,此时它与石头A相距______cm,与竹竿l相距______cm.
三.解答题(共4小题)
16.画图:试画出下列正多边形的所有对称轴,并完成表格,
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有______条对称轴.
17.光线以如图所示的角度a照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射.已知∠α=60°,∠β=50°,求∠γ.
18.设l1和l2是两面平行相对的镜子,如果把一个小球放在l1和l2之间(如图),试问:
(1)小球A在镜l1中的像A′在什么位置?
(2)小球A在镜l1中的像A′在镜l2中的像A″又在什么位置?分别画在图上;
(3)小球A和像A″之间的距离与l1和l2之间的距离有什么关系?
19.背景材料:【镜面对称:镜前的物体与其在镜中的像关于镜面对称】
(1)如果桌面上有一个用火柴摆出的等式,而你从前方墙上的镜子中看见的是如下式子:
那么你能立即对桌面上等式的正确性做出判断吗?______(填“正确”或“不正确”)
(2)如图①,镜前有黑、白两球,如果你用白球瞄准黑球在镜中的像,击出的白球就能经镜面反弹击中黑球;
如果你有两面互相垂直的镜子如图②,你想让击出的白球先后经两个镜面反弹,然后仍能击中黑球,那么你应该怎样瞄准?请仿照图①用箭头画出白球的运动的路线图;
(3)请利用轴对称知识解决下面问题:如图③,∠ABC=45°,D是射线BC上一点,BD=2cm,且E是BD的中点,点P是AB上一动点,求PE+PD的最小值.
参考答案
一.选择题(共8小题)
1.(2016 邵阳)下面四个手机应用图标中是轴对称图形的是( )
A.
B.
C.
D.
【分析】分别根据轴对称图形与中心对称图形的性质对各选项进行逐一分析即可.
【解答】解:A、既不是轴对称图形,也不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项错误;
C、既不是轴对称图形,也不是中心对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选D.
【点评】本题考查的是轴对称图形,熟知轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合是解答此题的关键.
2.(2016 西宁)在一些汉字的美术字中,有的是轴对称图形.下面四个美术字中可以看作轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可.
【解答】解:四个汉字中只有“善”字可以看作轴对称图形,
故选D.
【点评】考查了轴对称图形的知识,掌握轴对称图形的意义,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合.
3.(2016 梧州)下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解.
【解答】解:A、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
故选:B.
【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
4.(2016 台湾)若下列选项中的图形均为正多边形,则哪一个图形恰有4条对称轴?( )
A.
B.
C.
D.
【分析】直接利用轴对称图形的性质分析得出符合题意的答案.
【解答】解:A、正三角形有3条对称轴,故此选项错误;
B、正方形有4条对称轴,故此选项正确;
C、正六边形有6条对称轴,故此选项错误;
D、正八边形有8条对称轴,故此选项错误.
故选:B.
【点评】此题主要考查了轴对称图形,正确把握轴对称图形的定义是解题关键.
5.倡导节约,进入绿色,节约型社会,在食品包装、街道、宣传标语上随处可见节能、回收、绿色食品、节水的标志,在这些标志中,是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念对各图形判断后即可得解.
【解答】解:A、不是轴对称图形,故此选项错误;
B、不是轴对称图形,故此选项错误;
C、是轴对称图形,故此选项正确;
D、不是轴对称图形,故此选项错误;
故选:C.
【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,本题仔细观察图形是解题的关键.
6.窗花是我国传统民间艺术,下列窗花中,是轴对称图形的为( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.结合选项解答即可.
【解答】解:A、不是轴对称图形,故该选项错误;
B、是轴对称图形,故该选项正确;
C、不是轴对称图形,故该选项错误;
D、不是轴对称图形,故该选项错误.
故选B.
【点评】本题考查了轴对称图形的知识,解答本题的关键是掌握轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
7.下列图形中,轴对称图形的个数是( )
A.1个
B.2个
C.3个
D.4个
【分析】根据轴对称图形的概念求解.
【解答】解:第一个图形是轴对称图形;
第二个图形是轴对称图形;
第三个图形不是轴对称图形;
第四个图形是轴对称图形;
综上共有3个轴对称图形.
故选C.
【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
8.平行四边形,矩形,菱形,等边三角形,正方形中是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据轴对称图形的概念判断求解即可.
【解答】解:矩形、菱形、等边三角形、正方形都是轴对称图形,
所以共有4个图形是轴对称图形.
故选D.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
二.填空题(共7小题)
9.(2016 赤峰)下列图表是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 ①②③④ (填序号)
【分析】结合图象根据轴对称图形的概念解答即可.
【解答】解:根据轴对称图形的概念,可得出①②③④均为轴对称图形.
故答案为:①②③④.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
10.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有 4 种.
【分析】结合图象根据轴对称图形的概念求解即可.
【解答】解:根据轴对称图形的概念可知,一共有四种涂法,如下图所示:
.
故答案为:4.
【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
11.如果一个三角形是轴对称图形,且有一个角为60°,那么这个三角形是 等边三角形 ,它有 3 条对称轴.
【分析】先由该三角形是轴对称图形,可知该三角形是等腰三角形,再根据有一个内角是60°的等腰三角形是等边三角形,解答即可.
【解答】解:∵该三角形是轴对称图形,
∴该三角形是等腰三角形,
又∵该三角形有一个角为60°,
∴这个三角形是等边三角形,
∴这个三角形有3条对称轴.
故答案为:等边三角形,3.
【点评】本题考查了轴对称图形的知识,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
12.室内墙壁上挂一平面镜,明敏在平面镜内看到他背后墙上的时钟如图,则这时的实际时间是 3:40 .
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
【解答】解:根据镜面对称的性质,分析可得题中所显示的时刻与3:40成轴对称,所以此时实际时刻为:3:40.
故答案为:3:40.
【点评】本题考查了镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
13.如图是一个风筝的图案,它是轴对称图形,EF是对称轴.∠A=90°,∠AED=130°,∠C=45°,则∠BFC的度数为 140° .
【分析】利用轴对称图形的性质结合四边形内角和定理得出答案.
【解答】解:∵一个风筝的图案,它是轴对称图形,EF是对称轴.∠A=90°,∠AED=130°,∠C=45°,
∴∠D=90°,∠MED=65°,
∴∠DEF=115°,
∴∠CFN=360°﹣115°﹣90°﹣45°=110°
∴∠BFC的度数为:2(180°﹣110°)=140°.
故答案为:140°.
【点评】此题主要考查了轴对称图形的性质以及四边形内角和定理,熟练应用轴对称图形的性质是解题关键.
14.如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为 60 °.
【分析】要使白球反弹后能将黑球直接撞入袋中,则∠2=60°,根据∠1、∠2对称,则能求出∠1的度数.
【解答】解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=∠2=60°.
故答案是:60.
【点评】本题考查了同学们利用对称的性质解决问题的能力,根据入射角等于反射角得到∠1=∠2是解题的难点.
15.如图,石头A和石头B相距80cm,且关于竹竿l对称,一只电动青蛙在距竹竿30cm,距石头A为60cm的P1处,按如图所示的顺序循环跳跃.青蛙跳跃25次后停下,此时它与石头A相距 60 cm,与竹竿l相距 50 cm.
【分析】先根据对称的定义即可画出图形,找到25次后的位置P2,然后根据对称定义和梯形中位线定义求解距离.
【解答】
解:青蛙跳跃25次后停下,停在P2处,P2A=P1A=60cm,
∵点B是P3P4的中点,点A是P2P1的中点,
∴AB是梯形P1P2P3P4的中位线,
∴P2P3+P1P4=2AB,即(P2P3+P1P4)÷2=80,(P2P3+60)÷2=80,
解得:P2P3=100.P2与竹竿l相距100÷2=50cm.
故答案为:60、50.
【点评】本题考查了轴对称的性质及梯形的中位线定理,解答此题要明确在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等,另外要判断出AB是梯形P1P2P3P4的中位线.
三.解答题(共4小题)
16.画图:试画出下列正多边形的所有对称轴,并完成表格,
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有 n 条对称轴.
【分析】轴对称就是一个图形的一部分,沿着一条直线对折,能够和另一部分重合,这样的图形就是轴对称图形,这条直线就是对称轴,依据定义即可求解.
【解答】解:如图,
故填3,4,5,6,7,n.
【点评】正确理解轴对称图形的定义是解决本题的关键,本题是一个基础题.
17.光线以如图所示的角度a照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射.已知∠α=60°,∠β=50°,求∠γ.
【分析】利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角和角之间的相互转换来求解.
【解答】解:如答图所示,过A作MA⊥AC,垂足为A,
则∠1=90°﹣α=90°﹣60°=30°,
∴∠2=∠1=30°,
∴∠7=90°﹣30°=60°,
过B作BN⊥m,垂足为B,
∴∠3=90°﹣β=90°﹣50°=40°,
∴∠ABC=∠3+∠4=2∠3=2×40°=80°,
过C作CE⊥AC,垂足为C,
则∠5=∠6,∠BCD=2∠5+Y=∠7+∠ABC=60°+80°=140°,
∵∠5+Y=90°,
∴∠6=∠5=50°,
∴∠Y=90°﹣50°=40°.
【点评】本题考查镜面反射的原理与性质.需注意利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角,利用平行的性质把相应的角转移到一个三角形中求解.
18.设l1和l2是两面平行相对的镜子,如果把一个小球放在l1和l2之间(如图),试问:
(1)小球A在镜l1中的像A′在什么位置?
(2)小球A在镜l1中的像A′在镜l2中的像A″又在什么位置?分别画在图上;
(3)小球A和像A″之间的距离与l1和l2之间的距离有什么关系?
【分析】(1)A′应在和A关于L1对称的位置;
(2)A″应在和A′关于L2对称的位置;
(3)由对应点到对称轴的距离相等可得A和像A″之间的距离与l1和l2之间的距离的关系.
【解答】解:(1)∵A和A′关于L1对称,
∴A′应在L1的左边,到L1的距离等于A到L1的距离;
(2)A″应在和A′关于L2对称的位置,如图;
(3)∵A和A′关于L1对称,A′和A″关于L2对称,
∴AA′=2A′C,A′A″=2A′D,
∴AA″=A′A″﹣AA′=2(A′D﹣A′C)=2a.
【点评】考查镜面对称的知识;镜面对称是轴对称的一种特殊形式,关于镜面对称的两个物体到对称轴的距离相等.
19.背景材料:【镜面对称:镜前的物体与其在镜中的像关于镜面对称】
(1)如果桌面上有一个用火柴摆出的等式,而你从前方墙上的镜子中看见的是如下式子:
那么你能立即对桌面上等式的正确性做出判断吗? 正确 (填“正确”或“不正确”)
(2)如图①,镜前有黑、白两球,如果你用白球瞄准黑球在镜中的像,击出的白球就能经镜面反弹击中黑球;
如果你有两面互相垂直的镜子如图②,你想让击出的白球先后经两个镜面反弹,然后仍能击中黑球,那么你应该怎样瞄准?请仿照图①用箭头画出白球的运动的路线图;
(3)请利用轴对称知识解决下面问题:如图③,∠ABC=45°,D是射线BC上一点,BD=2cm,且E是BD的中点,点P是AB上一动点,求PE+PD的最小值.
【分析】(1)根据镜面对称原理即可判断答案;
(2)根据镜面对称就是轴对称关于镜面对称,把物体沿对称轴旋转180°推出即可;
(3)作D点关于AB的对称点D′点,连接D′E交AB于点P,此时PE+PD最小,利用勾股定理求得D′E的长即可.
【解答】解:(1)正确,
桌面上算式是152﹣20=132,
故答案为:正确.
(2)如图(2)所示:作白球A关于镜面ON的对称点C,作黑球B关于镜面OM的对称点D,连接CD交ON于E,交OM于F,连接AE、BF,
延AE﹣EF﹣FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球,
答:延AE﹣EF﹣FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球.
;
(3)如图(3),作D点关于AB的对称点D′点,连接D′E交AB于点P,
,此时PE+PD最小,
∵D点关于AC的对称点D′点,
∴BD=D′B,
∵BD=2cm,E是BD的中点,
∴D′B=2cm,EB=1cm,
∴D′E===,
∴PE+PD的最小值为.
【点评】本题主要考查对勾股定理,正方形的性质,轴对称的性质,线段垂直平分线的性质,镜面对称,轴对称﹣最短路线问题等知识点的理解和掌握,综合运用这些性质进行画图和推理是解此题的关键.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
