1.4 分数法 课件1
图片预览







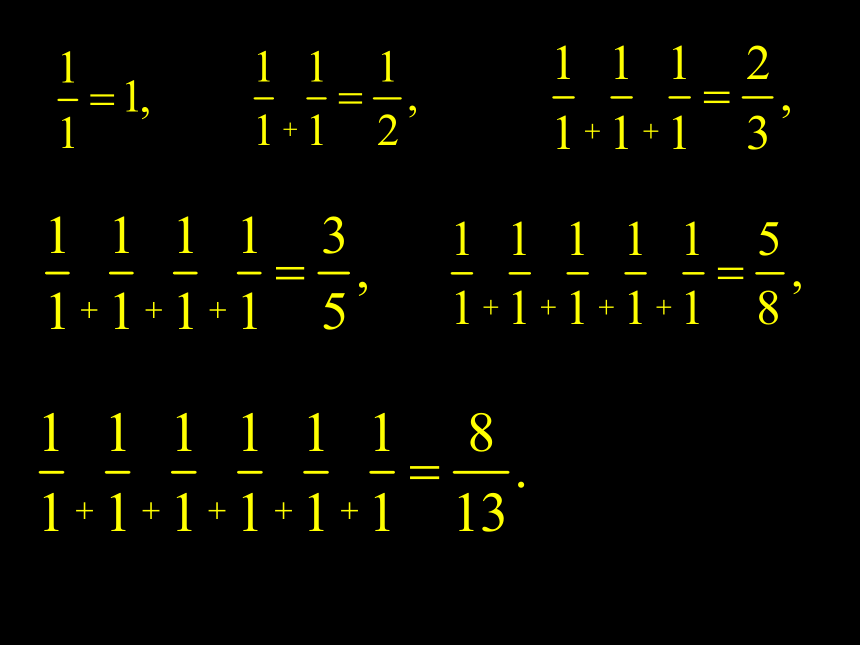

文档简介
课件26张PPT。选修4-7优选法与试验设计初步
第一讲 优选法
四.分数法问题提出 1.黄金分割法的基本原则是什么?两个试点关于存优范围的中心对称,且每次舍去的区间长度与舍去前的区间长度成比例. 2.用黄金分割法寻找最优点时,第一个试点选在何处?后续试点的数量值如何计算? 第一个试点在因素范围的0.618处;后续试点选在存优范围内,用“加两头,减中间”来确定数量值. 3.用黄金分割法确定试点时,n次试验后的精度δn为多少?δn=0.618n-1 4.黄金分割法操作简单实用,是一种重要的优选法,是寻找单因素单峰目标函数最佳点的主要方法.但是,如果因素范围是由一些离散的点组成,就不便甚至不能利用黄金分割法来寻找最佳点.用此,我们希望以黄金分割法为基础,再研究一个类似的方法来弥补黄金分割法的不足.分数法探究(一):分数法的概念 思考1:在配置某种清洗液时,需要加入某种材料.经验表明,加入量大于130ml肯定不好.用150ml的锥形量杯计量加入量,该量杯的量程分为15格,每格代表10ml,能否用0.618法找出这种材料的最优加入量?为什么?不方便,因为用0.618法算出的试点不是10ml的整数倍,锥形量杯难以精确计量. 思考2:0.618是黄金分割常数
的近似值,ω是方程ω2+ω-1=0的根,该方程可以作哪些变形?ω(ω+1)=1, 等.思考3:将等式 右边的ω反复
用 代替,可得什么关系式?思考4:上式右边是一个繁分式,叫做无穷连分数,为了书写简便,记作
,那么这个无穷分数的前6项
分别为多少?前一项的分母等于后一项的分子; F0=F1=1, . 思考6:上述数列{Fn}叫做斐波那契数
列,随着n的增大, 的值与ω有什么关系?逐渐趋向于ω思考7:分数 可作为ω的近似值,而
且n越大近似程度越高,数列 称为
ω的渐近分数列, 称为ω的第n项渐
近分数.如果用0.618法确定试点不方便,可以用哪些数代替0.618?用ω的渐近分数 思考8:在前述“配置清洗液”问题中,因素范围是0~130ml,锥形量杯能精确计量10ml的整数倍,用哪个渐近分数来代替0.618选取试点最合适? 思考9:用 代替0.618,第1试点和第2
试点对应的加入量分别为多少ml?若第1试点是好点,则第3试点对应的加入量为多少ml? x2=0+130-80=50 x3=50+130-80=100思考10:在优选法中,用渐近分数近似代替0.618确定试点的方法叫做分数法,那么在什么情况下使用分数法? 因素范围由一些离散的、间隔不等的点组成,试点只能取某些特定值.探究(二):分数法的操作原理 思考1:在测试某设备的线路中,要选一个电阻,但测试者手里只有阻值为0.5KΩ,1KΩ,1.3KΩ,2KΩ,3KΩ,5KΩ,5.5KΩ等七种阻值不等的定值电阻,用分数法优选这个阻值有何困难?如何解决?阻值间隔不均匀,电阻个数不是斐波那契数. 把这些电阻由小到大排序,并在两端各增加一个虚点,使因素范围凑成8格.
阻值 0.5 1 1.3 2 3 5 5.5
排序 0 1 2 3 4 5 6 7 83KΩ,1.3KΩ.思考2:通过上述处理,可以把阻值优
选变为排列序号优选,用渐近分数 代
替0.618确定试点,第1个试点选取哪个阻值的电阻?第2个试点选取哪个阻值的电阻? 思考3:如果第2个试点是好点,则第3个试点选取哪个阻值的电阻?如果第1个试点是好点,则第3个试点选取哪个阻值的电阻? 5KΩ.1KΩ.思考4:分数法的基本思想是用适当的渐近分数代替0.618,再类似黄金分割法的操作原理选取试点.设某试验的因素范围是[0,1],如果只能做1次试验,则应取哪个渐近分数代替0.618?试点选在何处?精度为多少?精度为0.5. 思考5:设某试验的因素范围是[0,1],如果只能做2次试验,则应取哪个渐近分数代替0.618?两个试点分别选在何处?精度为多少?第1试点选在 处,第2试点选在 处,
精度为 .思考6:如果只能做3次试验,则应取哪个渐近分数代替0.618?精度为多少?一般地,如果只能做k次试验,则应取哪个渐近分数代替0.618?精度为多少?渐近分数取 ,精度为 ; 渐近分数取 ,精度为 .思考7:用分数法安排试点时,若可能的试点总数正好是某一个Fn-1,则第1,2个试点分别选哪个点?经过两次试验后,存优范围中还剩下多少个试点可能是最佳点?第Fn-1和Fn-2点,剩Fn-1-1个试点. 思考8:在Fn-1个可能的试点中,最多做多少次试验就能找到其中的最佳点?最多做n-1次试验 思考9:若可能的试点总数大于某一个 Fn-1,且小于某一个Fn+1-1,用分数法安排试点时应作如何处理?把所有可能的试点减少为Fn-1个, 或增设几个虚点凑成Fn+1-1个.思考10:一般地,用分数法安排试点的操作步骤如何?(1)将试点个数调整为Fn-1个; (2)用 代替0.618确定第一个试点; (3)用“加两头,减中间”的方法确定后续试点.思考11:对目标函数为单峰的情形,用分数法寻找最佳点的试验次数与试点个数有什么关系?(1)当因素范围内有Fn+1-1个试点时,最多只需作n次试验就能找出其中的最佳点.(2)通过n次试验,最多能从Fn+1-1个试点中保证找出最佳点.(3)只有按照分数法安排试点,才能通过n次试验保证从Fn+1-1个试点中找出最佳点.理论迁移 例 某化工厂拟对某一化工产品进行技术改良,需要优选加工温度,试验范围定为60~80°C,精度要求±1°,技术员准备用分数法进行优选.
(1)如何安排试验?
(2)最多通过几次试验就可以找出最佳点?
(3)若最佳点为70°C,求各试点的值.小结作业 1.分数法适用于单因素单峰函数的因素范围由一些离散的点组成,试点只能取某些特定值的情形,其基本思想是用适当的渐近分数代替0.618,然后按类似黄金分割法的操作原理选取试点. 即先用渐近分数确定第一个试点,后续试点可以用“加两头,减中间”的方法来确定. 2.现实中,由于时间、人力、物力和财力的关系,往往使试验次数受到限制,这种情况下采用分数法可以达到较好的效果.当试点个数一定时,用分数法找出其中的最佳点的试验次数最少. 3.若因素范围内的试点将试验范围所分的段数不是斐波那契数,则可以通过减少试点数或增加虚点数凑成斐波那契数.作业:
P17习题1.4:1,2,3.
第一讲 优选法
四.分数法问题提出 1.黄金分割法的基本原则是什么?两个试点关于存优范围的中心对称,且每次舍去的区间长度与舍去前的区间长度成比例. 2.用黄金分割法寻找最优点时,第一个试点选在何处?后续试点的数量值如何计算? 第一个试点在因素范围的0.618处;后续试点选在存优范围内,用“加两头,减中间”来确定数量值. 3.用黄金分割法确定试点时,n次试验后的精度δn为多少?δn=0.618n-1 4.黄金分割法操作简单实用,是一种重要的优选法,是寻找单因素单峰目标函数最佳点的主要方法.但是,如果因素范围是由一些离散的点组成,就不便甚至不能利用黄金分割法来寻找最佳点.用此,我们希望以黄金分割法为基础,再研究一个类似的方法来弥补黄金分割法的不足.分数法探究(一):分数法的概念 思考1:在配置某种清洗液时,需要加入某种材料.经验表明,加入量大于130ml肯定不好.用150ml的锥形量杯计量加入量,该量杯的量程分为15格,每格代表10ml,能否用0.618法找出这种材料的最优加入量?为什么?不方便,因为用0.618法算出的试点不是10ml的整数倍,锥形量杯难以精确计量. 思考2:0.618是黄金分割常数
的近似值,ω是方程ω2+ω-1=0的根,该方程可以作哪些变形?ω(ω+1)=1, 等.思考3:将等式 右边的ω反复
用 代替,可得什么关系式?思考4:上式右边是一个繁分式,叫做无穷连分数,为了书写简便,记作
,那么这个无穷分数的前6项
分别为多少?前一项的分母等于后一项的分子; F0=F1=1, . 思考6:上述数列{Fn}叫做斐波那契数
列,随着n的增大, 的值与ω有什么关系?逐渐趋向于ω思考7:分数 可作为ω的近似值,而
且n越大近似程度越高,数列 称为
ω的渐近分数列, 称为ω的第n项渐
近分数.如果用0.618法确定试点不方便,可以用哪些数代替0.618?用ω的渐近分数 思考8:在前述“配置清洗液”问题中,因素范围是0~130ml,锥形量杯能精确计量10ml的整数倍,用哪个渐近分数来代替0.618选取试点最合适? 思考9:用 代替0.618,第1试点和第2
试点对应的加入量分别为多少ml?若第1试点是好点,则第3试点对应的加入量为多少ml? x2=0+130-80=50 x3=50+130-80=100思考10:在优选法中,用渐近分数近似代替0.618确定试点的方法叫做分数法,那么在什么情况下使用分数法? 因素范围由一些离散的、间隔不等的点组成,试点只能取某些特定值.探究(二):分数法的操作原理 思考1:在测试某设备的线路中,要选一个电阻,但测试者手里只有阻值为0.5KΩ,1KΩ,1.3KΩ,2KΩ,3KΩ,5KΩ,5.5KΩ等七种阻值不等的定值电阻,用分数法优选这个阻值有何困难?如何解决?阻值间隔不均匀,电阻个数不是斐波那契数. 把这些电阻由小到大排序,并在两端各增加一个虚点,使因素范围凑成8格.
阻值 0.5 1 1.3 2 3 5 5.5
排序 0 1 2 3 4 5 6 7 83KΩ,1.3KΩ.思考2:通过上述处理,可以把阻值优
选变为排列序号优选,用渐近分数 代
替0.618确定试点,第1个试点选取哪个阻值的电阻?第2个试点选取哪个阻值的电阻? 思考3:如果第2个试点是好点,则第3个试点选取哪个阻值的电阻?如果第1个试点是好点,则第3个试点选取哪个阻值的电阻? 5KΩ.1KΩ.思考4:分数法的基本思想是用适当的渐近分数代替0.618,再类似黄金分割法的操作原理选取试点.设某试验的因素范围是[0,1],如果只能做1次试验,则应取哪个渐近分数代替0.618?试点选在何处?精度为多少?精度为0.5. 思考5:设某试验的因素范围是[0,1],如果只能做2次试验,则应取哪个渐近分数代替0.618?两个试点分别选在何处?精度为多少?第1试点选在 处,第2试点选在 处,
精度为 .思考6:如果只能做3次试验,则应取哪个渐近分数代替0.618?精度为多少?一般地,如果只能做k次试验,则应取哪个渐近分数代替0.618?精度为多少?渐近分数取 ,精度为 ; 渐近分数取 ,精度为 .思考7:用分数法安排试点时,若可能的试点总数正好是某一个Fn-1,则第1,2个试点分别选哪个点?经过两次试验后,存优范围中还剩下多少个试点可能是最佳点?第Fn-1和Fn-2点,剩Fn-1-1个试点. 思考8:在Fn-1个可能的试点中,最多做多少次试验就能找到其中的最佳点?最多做n-1次试验 思考9:若可能的试点总数大于某一个 Fn-1,且小于某一个Fn+1-1,用分数法安排试点时应作如何处理?把所有可能的试点减少为Fn-1个, 或增设几个虚点凑成Fn+1-1个.思考10:一般地,用分数法安排试点的操作步骤如何?(1)将试点个数调整为Fn-1个; (2)用 代替0.618确定第一个试点; (3)用“加两头,减中间”的方法确定后续试点.思考11:对目标函数为单峰的情形,用分数法寻找最佳点的试验次数与试点个数有什么关系?(1)当因素范围内有Fn+1-1个试点时,最多只需作n次试验就能找出其中的最佳点.(2)通过n次试验,最多能从Fn+1-1个试点中保证找出最佳点.(3)只有按照分数法安排试点,才能通过n次试验保证从Fn+1-1个试点中找出最佳点.理论迁移 例 某化工厂拟对某一化工产品进行技术改良,需要优选加工温度,试验范围定为60~80°C,精度要求±1°,技术员准备用分数法进行优选.
(1)如何安排试验?
(2)最多通过几次试验就可以找出最佳点?
(3)若最佳点为70°C,求各试点的值.小结作业 1.分数法适用于单因素单峰函数的因素范围由一些离散的点组成,试点只能取某些特定值的情形,其基本思想是用适当的渐近分数代替0.618,然后按类似黄金分割法的操作原理选取试点. 即先用渐近分数确定第一个试点,后续试点可以用“加两头,减中间”的方法来确定. 2.现实中,由于时间、人力、物力和财力的关系,往往使试验次数受到限制,这种情况下采用分数法可以达到较好的效果.当试点个数一定时,用分数法找出其中的最佳点的试验次数最少. 3.若因素范围内的试点将试验范围所分的段数不是斐波那契数,则可以通过减少试点数或增加虚点数凑成斐波那契数.作业:
P17习题1.4:1,2,3.
