1.3 黄金分割法——0.618法 课件1
文档属性
| 名称 | 1.3 黄金分割法——0.618法 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 89.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-20 00:00:00 | ||
图片预览








文档简介
课件28张PPT。选修4-7优选法与试验设计初步
第一讲 优选法
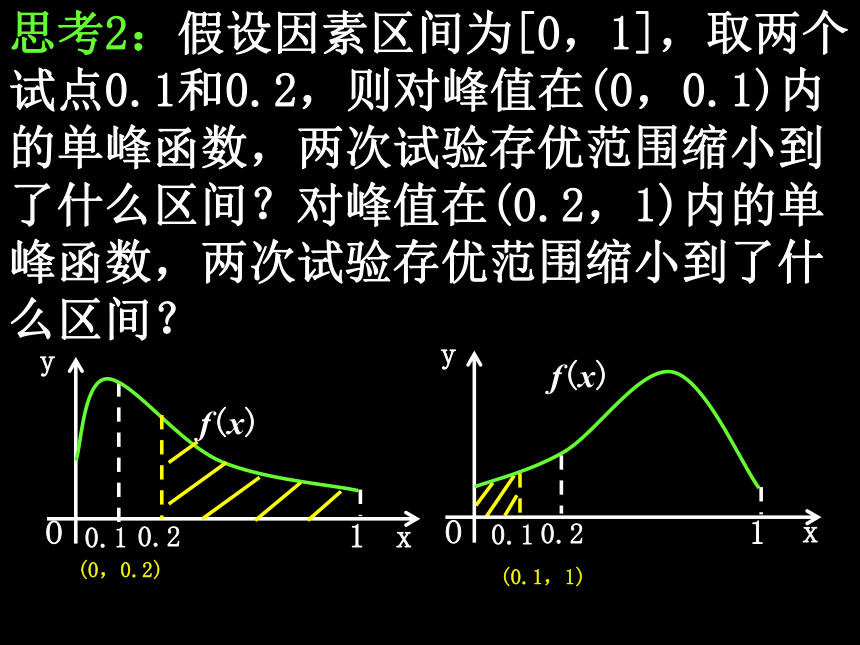
三.黄金分割法——0.618法问题提出 1.优选法的含意是什么?利用数学原理,合理安排试验,以最少的实验次数迅速找到最佳点的科学试验方法. 2.区间[a,b]上的单峰函数的基本特点是什么?函数在区间[a,b]上只有唯一的最大(小)值点C,且在点C的两侧单调,并具有相反的单调性. 3.好点、差点和单峰函数存优范围的含义分别是什么? 好点:两个试点中效果较好的点; 差点:两个试点中效果较差的点; 存优范围:以差点为分界点,把因素范 围分成两部分,好点所在 部分对应的范围. 4.优选法的基本原则是以最少的实验次数迅速找到最佳点,在实际问题中,应采取什么办法贯彻这个原则?对具有单峰性的试验,如何安排试点才能迅速找到最佳点?这才是优选法的核心内容,也是我们必须解决的问题.黄金分割法探究(一):黄金分割常数 思考1:对于单峰函数,最佳点与好点必在差点的同侧,从而可以通过不断缩小存优范围来寻找最佳点,具体如何操作?先在因素范围[a,b]内任选两点各做一次试验,根据试验结果确定好点与差点,在差点处把[a,b]分成两段,截掉不含好点的一段,留下存优范围[a1,b1]再在[a1,b1]内重复上述工作,….思考2:假设因素区间为[0,1],取两个试点0.1和0.2,则对峰值在(0,0.1)内的单峰函数,两次试验存优范围缩小到了什么区间?对峰值在(0.2,1)内的单峰函数,两次试验存优范围缩小到了什么区间? (0,0.2) (0.1,1) 思考3:上述结果表明,如果试点选取是随意的,则对寻找单峰函数最佳点的效率会产生一定的影响.由于在试验之前无法预知哪个试点是好点,为了克服盲目性和侥幸心理,在每次选取两个试点时,你认为这两个试点应具有什么相对位置关系为好?关于区间中点对称 思考4:在一个区间内关于中点对称的两点有无数对,实践表明,两个试点离中点太近或太远,都不利于很快接近最佳点.我们设想:每次舍去的区间长度与舍去前的区间长度之比为常数.对单峰函数,若两个试点的试验结果一样,应如何舍去区间? 同时舍去两个试点外侧的区间.思考5:在因素区间[a,b]内选取两个试点x1和x2,且x1>x2,由点x1和x2关于区间[a,b]的中心对称,可得什么关系?舍去的区间长度为多少? x2-a=b-x1 思考6:不妨设x2是好点,x1是差点,则舍去的区间是什么?存优范围是什么?再在存优范围内[a,x1]内做试验要取几个试点?存优范围是[a,x1] 舍去(x1,b] 取一个试点 思考7:在存优范围[a,x1]内取第三个试点x3,则点x2与x3的相对位置关系如何?舍去的区间长度为多少?关于区间[a,x1]的中心对称,且点x3在点x2左侧,舍去的区间长度为x1-x2.思考8:根据按比例舍去原则,可得什么等式?两次舍弃后的存优范围占舍弃前全区间的比例数.探究(二):黄金分割法 在存优范围内取黄金分割点为试点. 思考2:炼钢时通过加入含有特定化学元素的材料,使练出的钢满足一定的指标要求.假设为了炼出某种特定用途的钢,每吨需要加入某元素的量在1000g到2000g之间,若以1g为间隔,把所有的可能性都做一遍试验来寻找最优点,这种方法称为均分法,利用均分法寻找最优点有什么缺点?试验次数太多,在时间、人力和物力上造成浪费.思考3:用一张纸条表示1000~2000g,以1000为起点标出刻度,如何确定第一试点x1和第二试点x2的值?13821618 x1=1000+0.618×(2000-1000) =1618(g), x2=1000+2000-x1=1382(g).思考4:如果称因素范围的左右两端点值分别为小头和大头,那么x1和x2的直观表达式如何?x1=小+0.618×(大-小), x2=小+大-x1.思考5:用黄金分割法确定第一试点x1后,x2的值相当于“加两头,减中间”.类似地,在确定第n个试点xn时,如果存优范围内相应的好点是xm,则xn等于什么?xn=小+大-xm思考6:对前述炼钢问题,比较第一、二次试验结果,如果第二试点x2是好点,则第三试点x3的值如何计算? x3=1000+1618-1382=1236(g) 思考7:比较第二、三次试验结果,如果第二试点x2仍是好点,则第四试点x4的值如何计算?
x4=1236+1618-1382=1472(g)思考8:用0.618法寻找最佳点时,虽然不能保证在有限次内准确找到最佳点,但随着试验次数的增加,存优范围会越来越小,若用一个数据δn来刻画n次试验后的精度,以此衡量一种试验方法的效率,则δn应如何计算?思考9:用0.618法确定试点时,n次试验后的精度δn为多少? δn=0.618n-1思考10:用0.618法寻找最佳点时,若给定精度δ,为了达到这个精度,至少要做多少次试验?理论迁移 例1 已知某因素范围是[100,1100],用黄金分割法寻找最佳点,已知前6次试验后的好点包含在区间[700,750]内,求第6次试验后的存优范围.[684,774] 例2 调酒师为了调制一种鸡尾酒,每100kg烈性酒中需要加入柠檬汁的量在1kg到2kg之间,用0.618法寻找它的最佳加入量,要求加入柠檬汁的误差不超出1g,问需要做多少次试验?需要做19次试验 例3 在用0.618法寻找最佳点的过程中,若某次试验后的存优范围是[2,b]且2.382是这个存优范围内的一个好点,求b的值.b=2.618或b=3. 小结作业 1.建立黄金分割法的基本原则是:两个试点关于存优范围的中心对称,且每次舍去的区间长度与舍去前的区间长度成比例. 2.黄金分割法主要适用于单因素单峰目标函数,第一个试点确定在因素范围的0.618处,后续试点可以用“加两头,减中间”来确定. 3.试验方法的效率常用精度δn来反映,在相同试验次数下,精度越高,方法越好.作业:
P10习题1.3:1,2,3.
第一讲 优选法
三.黄金分割法——0.618法问题提出 1.优选法的含意是什么?利用数学原理,合理安排试验,以最少的实验次数迅速找到最佳点的科学试验方法. 2.区间[a,b]上的单峰函数的基本特点是什么?函数在区间[a,b]上只有唯一的最大(小)值点C,且在点C的两侧单调,并具有相反的单调性. 3.好点、差点和单峰函数存优范围的含义分别是什么? 好点:两个试点中效果较好的点; 差点:两个试点中效果较差的点; 存优范围:以差点为分界点,把因素范 围分成两部分,好点所在 部分对应的范围. 4.优选法的基本原则是以最少的实验次数迅速找到最佳点,在实际问题中,应采取什么办法贯彻这个原则?对具有单峰性的试验,如何安排试点才能迅速找到最佳点?这才是优选法的核心内容,也是我们必须解决的问题.黄金分割法探究(一):黄金分割常数 思考1:对于单峰函数,最佳点与好点必在差点的同侧,从而可以通过不断缩小存优范围来寻找最佳点,具体如何操作?先在因素范围[a,b]内任选两点各做一次试验,根据试验结果确定好点与差点,在差点处把[a,b]分成两段,截掉不含好点的一段,留下存优范围[a1,b1]再在[a1,b1]内重复上述工作,….思考2:假设因素区间为[0,1],取两个试点0.1和0.2,则对峰值在(0,0.1)内的单峰函数,两次试验存优范围缩小到了什么区间?对峰值在(0.2,1)内的单峰函数,两次试验存优范围缩小到了什么区间? (0,0.2) (0.1,1) 思考3:上述结果表明,如果试点选取是随意的,则对寻找单峰函数最佳点的效率会产生一定的影响.由于在试验之前无法预知哪个试点是好点,为了克服盲目性和侥幸心理,在每次选取两个试点时,你认为这两个试点应具有什么相对位置关系为好?关于区间中点对称 思考4:在一个区间内关于中点对称的两点有无数对,实践表明,两个试点离中点太近或太远,都不利于很快接近最佳点.我们设想:每次舍去的区间长度与舍去前的区间长度之比为常数.对单峰函数,若两个试点的试验结果一样,应如何舍去区间? 同时舍去两个试点外侧的区间.思考5:在因素区间[a,b]内选取两个试点x1和x2,且x1>x2,由点x1和x2关于区间[a,b]的中心对称,可得什么关系?舍去的区间长度为多少? x2-a=b-x1 思考6:不妨设x2是好点,x1是差点,则舍去的区间是什么?存优范围是什么?再在存优范围内[a,x1]内做试验要取几个试点?存优范围是[a,x1] 舍去(x1,b] 取一个试点 思考7:在存优范围[a,x1]内取第三个试点x3,则点x2与x3的相对位置关系如何?舍去的区间长度为多少?关于区间[a,x1]的中心对称,且点x3在点x2左侧,舍去的区间长度为x1-x2.思考8:根据按比例舍去原则,可得什么等式?两次舍弃后的存优范围占舍弃前全区间的比例数.探究(二):黄金分割法 在存优范围内取黄金分割点为试点. 思考2:炼钢时通过加入含有特定化学元素的材料,使练出的钢满足一定的指标要求.假设为了炼出某种特定用途的钢,每吨需要加入某元素的量在1000g到2000g之间,若以1g为间隔,把所有的可能性都做一遍试验来寻找最优点,这种方法称为均分法,利用均分法寻找最优点有什么缺点?试验次数太多,在时间、人力和物力上造成浪费.思考3:用一张纸条表示1000~2000g,以1000为起点标出刻度,如何确定第一试点x1和第二试点x2的值?13821618 x1=1000+0.618×(2000-1000) =1618(g), x2=1000+2000-x1=1382(g).思考4:如果称因素范围的左右两端点值分别为小头和大头,那么x1和x2的直观表达式如何?x1=小+0.618×(大-小), x2=小+大-x1.思考5:用黄金分割法确定第一试点x1后,x2的值相当于“加两头,减中间”.类似地,在确定第n个试点xn时,如果存优范围内相应的好点是xm,则xn等于什么?xn=小+大-xm思考6:对前述炼钢问题,比较第一、二次试验结果,如果第二试点x2是好点,则第三试点x3的值如何计算? x3=1000+1618-1382=1236(g) 思考7:比较第二、三次试验结果,如果第二试点x2仍是好点,则第四试点x4的值如何计算?
x4=1236+1618-1382=1472(g)思考8:用0.618法寻找最佳点时,虽然不能保证在有限次内准确找到最佳点,但随着试验次数的增加,存优范围会越来越小,若用一个数据δn来刻画n次试验后的精度,以此衡量一种试验方法的效率,则δn应如何计算?思考9:用0.618法确定试点时,n次试验后的精度δn为多少? δn=0.618n-1思考10:用0.618法寻找最佳点时,若给定精度δ,为了达到这个精度,至少要做多少次试验?理论迁移 例1 已知某因素范围是[100,1100],用黄金分割法寻找最佳点,已知前6次试验后的好点包含在区间[700,750]内,求第6次试验后的存优范围.[684,774] 例2 调酒师为了调制一种鸡尾酒,每100kg烈性酒中需要加入柠檬汁的量在1kg到2kg之间,用0.618法寻找它的最佳加入量,要求加入柠檬汁的误差不超出1g,问需要做多少次试验?需要做19次试验 例3 在用0.618法寻找最佳点的过程中,若某次试验后的存优范围是[2,b]且2.382是这个存优范围内的一个好点,求b的值.b=2.618或b=3. 小结作业 1.建立黄金分割法的基本原则是:两个试点关于存优范围的中心对称,且每次舍去的区间长度与舍去前的区间长度成比例. 2.黄金分割法主要适用于单因素单峰目标函数,第一个试点确定在因素范围的0.618处,后续试点可以用“加两头,减中间”来确定. 3.试验方法的效率常用精度δn来反映,在相同试验次数下,精度越高,方法越好.作业:
P10习题1.3:1,2,3.
