1.3 黄金分割法——0.618法 课件2
文档属性
| 名称 | 1.3 黄金分割法——0.618法 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 138.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-20 00:00:00 | ||
图片预览



文档简介
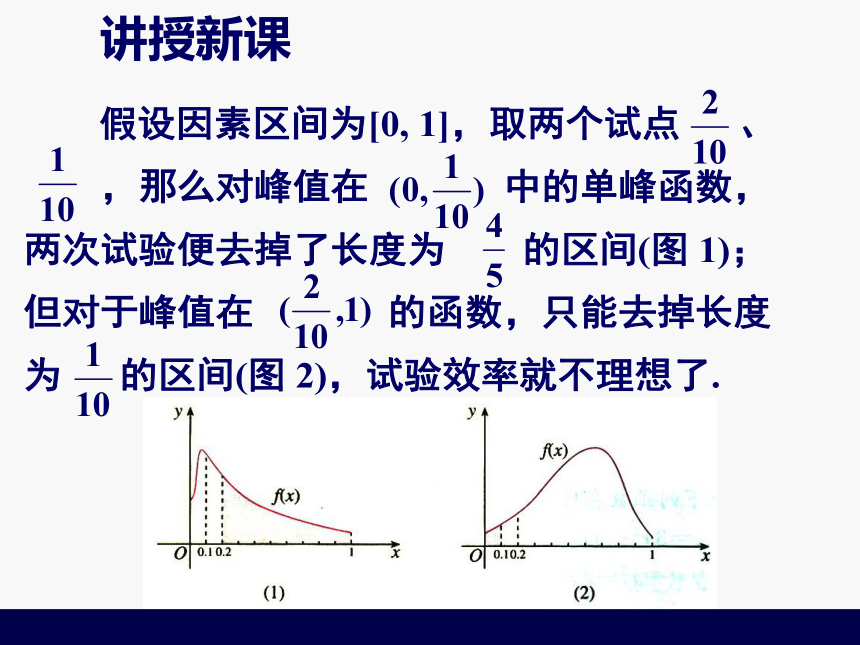
课件15张PPT。第一讲 优选法三、黄金分割法——0.618法讲授新课 一、黄金分割常数 对于一般的单峰函数,如何安排
试点才能迅速找到最佳点?讲授新课讲授新课 怎样选取各个试点,可以最快地
达到或接近最佳点? 在安排试点时,最好使两个试点
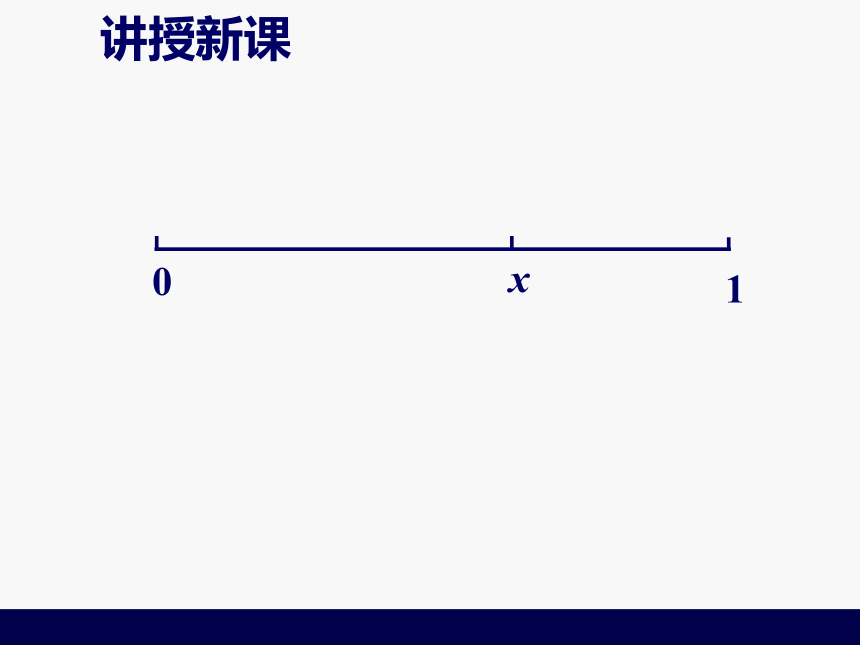
关于[a,b]的中心 对称. 为了使每次去掉的区间有一定的
规律性,我们这样来考虑:每次舍去
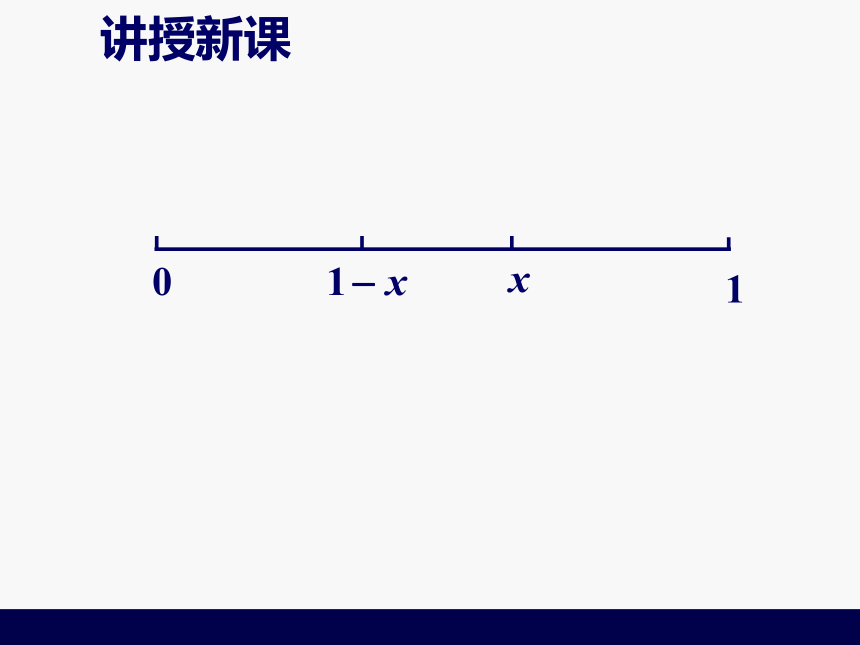
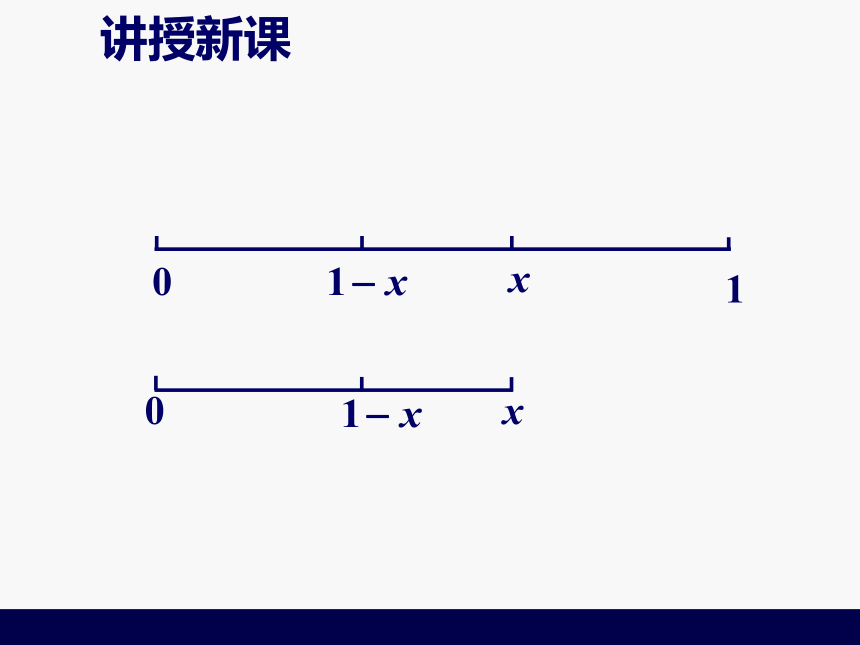
的区间占舍去前的区间的比例数相同.讲授新课01讲授新课01讲授新课010x讲授新课010x讲授新课010x讲授新课010x第1个试验点:0.618处,
后续试点: “加两头,减中间”讲授新课黄金分割常数:,用?表示. 试验方法中,利用黄金分割常数?
确定试点的方法叫做黄金分割法.由于是无理数,具体应用时,我们往往取其近似值0.618.相应地,也把黄
金分割法叫做0.618法.讲授新课 二、黄金分割法——0.618法例.炼钢时通过加入含有特定化学元素的
材料,使炼出的钢满足一定的指标要求.
假设为了炼出某种特定用途的钢,每吨
需要加入某元素的量在1000g到2000g之
间,问如何通过试验的方法找到它的最
优加入量?讲授新课 我们用存优范围与原始范围的比值
来衡量一种试验方法的效率,这个比值
叫做精度,即n次试验后的精度为 用0.618法确定试点时,从第2次试验
开始,每一次试验都把存优范围缩小为原
来的0.618.因此,n次试验后的精度为讲授新课 一般地,给定精度?,为了达到这
个精度,所要做的试验次数n满足即所以 黄金分割法适用目标函数为单峰的
情形,第1个试验点确定在因素范围的
0.618处,后续试点可以用“加两头,减
中间”的方法来确定.课后作业1.阅读教材P. 5-P.10;
试点才能迅速找到最佳点?讲授新课讲授新课 怎样选取各个试点,可以最快地
达到或接近最佳点? 在安排试点时,最好使两个试点
关于[a,b]的中心 对称. 为了使每次去掉的区间有一定的
规律性,我们这样来考虑:每次舍去
的区间占舍去前的区间的比例数相同.讲授新课01讲授新课01讲授新课010x讲授新课010x讲授新课010x讲授新课010x第1个试验点:0.618处,
后续试点: “加两头,减中间”讲授新课黄金分割常数:,用?表示. 试验方法中,利用黄金分割常数?
确定试点的方法叫做黄金分割法.由于是无理数,具体应用时,我们往往取其近似值0.618.相应地,也把黄
金分割法叫做0.618法.讲授新课 二、黄金分割法——0.618法例.炼钢时通过加入含有特定化学元素的
材料,使炼出的钢满足一定的指标要求.
假设为了炼出某种特定用途的钢,每吨
需要加入某元素的量在1000g到2000g之
间,问如何通过试验的方法找到它的最
优加入量?讲授新课 我们用存优范围与原始范围的比值
来衡量一种试验方法的效率,这个比值
叫做精度,即n次试验后的精度为 用0.618法确定试点时,从第2次试验
开始,每一次试验都把存优范围缩小为原
来的0.618.因此,n次试验后的精度为讲授新课 一般地,给定精度?,为了达到这
个精度,所要做的试验次数n满足即所以 黄金分割法适用目标函数为单峰的
情形,第1个试验点确定在因素范围的
0.618处,后续试点可以用“加两头,减
中间”的方法来确定.课后作业1.阅读教材P. 5-P.10;
