华师大版九年级上23.3.3相似三角形的性质课件
文档属性
| 名称 | 华师大版九年级上23.3.3相似三角形的性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 712.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-21 00:00:00 | ||
图片预览



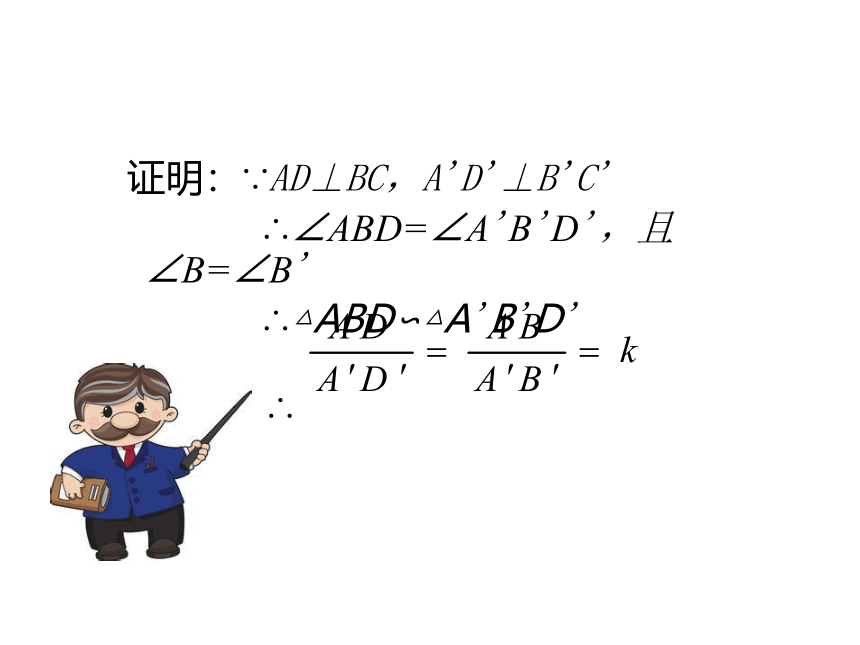

文档简介
课件10张PPT。23.3.3 相似三角形的性质 第24章 图形的相似 驶向胜利的彼岸
23.3.3 相似三角形的性质复习导入1.相似三角形的判定方法有哪些?
2.相似三角形有哪些性质?
3.三角形中的主要线段有哪些?探索新知如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中AD、A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么关系。
相似三角形的对应高的比等于相似比.证明:∵AD⊥BC,A'D'⊥B'C'
∴∠ABD=∠A'B'D',且∠B=∠B'
∴△ABD∽△A'B'D'
∴
2.若将上图中的高改为中线、角分线,那么它们对应中线的比,对应角平分线的比等于多少?
结论:相似三角形对应中线的比等于相似比.
结论:相似三角形对应角的角平分线的比等于相似比.3.相似三角形的周长比等于相似比.
4.相似三角形的面积比等于相似比的平方.
巩固练习1.教材第72页练习第1、2题。
3.若两个相似三角最大边长分别为35cm和14cm,它们的周长差为60cm,则较大的三角形的周长是多少?
4.在△ABC中,已知D在AB上,E在AC上,且DE∥BC,AB=30m,BD=18m,△ABC的周长为80m,面积为100m2,求△ADE的周长和面积。答案:1.3∶5. 2.0.4 0.4 0.4 0.16. 3.100cm 4.32 16归纳小结利用相似三角形的性质解题时,应特别注意“对应”,切忌混淆对应边的比与相似比中的前后项的位置。课后作业观察可能导致发现,观察将揭示某种规则、模式或定律。
——波利亚
23.3.3 相似三角形的性质复习导入1.相似三角形的判定方法有哪些?
2.相似三角形有哪些性质?
3.三角形中的主要线段有哪些?探索新知如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中AD、A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么关系。
相似三角形的对应高的比等于相似比.证明:∵AD⊥BC,A'D'⊥B'C'
∴∠ABD=∠A'B'D',且∠B=∠B'
∴△ABD∽△A'B'D'
∴
2.若将上图中的高改为中线、角分线,那么它们对应中线的比,对应角平分线的比等于多少?
结论:相似三角形对应中线的比等于相似比.
结论:相似三角形对应角的角平分线的比等于相似比.3.相似三角形的周长比等于相似比.
4.相似三角形的面积比等于相似比的平方.
巩固练习1.教材第72页练习第1、2题。
3.若两个相似三角最大边长分别为35cm和14cm,它们的周长差为60cm,则较大的三角形的周长是多少?
4.在△ABC中,已知D在AB上,E在AC上,且DE∥BC,AB=30m,BD=18m,△ABC的周长为80m,面积为100m2,求△ADE的周长和面积。答案:1.3∶5. 2.0.4 0.4 0.4 0.16. 3.100cm 4.32 16归纳小结利用相似三角形的性质解题时,应特别注意“对应”,切忌混淆对应边的比与相似比中的前后项的位置。课后作业观察可能导致发现,观察将揭示某种规则、模式或定律。
——波利亚
