3.1 用树状图或表格求概率课件( 第2课时)
文档属性
| 名称 | 3.1 用树状图或表格求概率课件( 第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 424.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-21 22:11:21 | ||
图片预览






文档简介
课件14张PPT。第三章 概率的进一步认识3.1 用树状图或表格求概率(二)
温故知新 上节课,你学会了用什么方法求某个事件发生的概率.答:树状图、列表格.问题提出 例1 小明、小颖和小凡做“石头、剪刀、布”的游戏,游戏规则如下:
由小明和小颖玩“石头、剪刀、布”游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者.
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?解法1:因为小明和小颖每次出这三种手势的可能性相同,所以可以利用树状图列出所有可能出现的结果:石头
剪刀
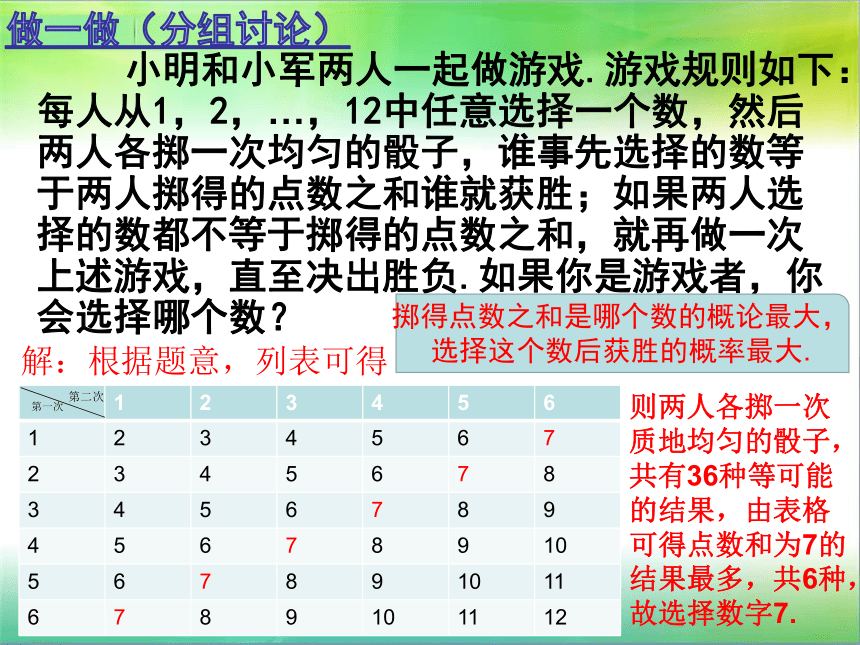
布开始此颜色小凡获胜此颜色小明获胜此颜色小颖获胜所以,这个游戏对三人是公平的.总共有9种可能的结果,每种结果出现的可能性相同.由树状图可知:解法2:根据题意列表如下:由列表可知:所以,这个游戏对三人是公平的.做一做(分组讨论) 小明和小军两人一起做游戏.游戏规则如下:每人从1,2,…,12中任意选择一个数,然后两人各掷一次均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负.如果你是游戏者,你会选择哪个数?掷得点数之和是哪个数的概论最大,选择这个数后获胜的概率最大.解:根据题意,列表可得则两人各掷一次质地均匀的骰子,共有36种等可能的结果,由表格可得点数和为7的结果最多,共6种,故选择数字7.第一次第二次 有三张大小一样而画面不同的画片,先将每一张从中间剪开,分成上下两部分;然后把三张画片的上半部分都放在第一个盒子中,把下半部分都放在第二个盒子中.分别摇匀后,从每个盒子中各随机地摸出一张,求这两张恰好能拼成原来的一幅画的概率随堂练习P64解:列表格得:第一个盒子第二个盒子子∴共有9种不同的拼法
∴能拼成一幅画的概率是 .中考链接:1. 定义:百位、十位、个位上的数字从左到右依次增大的三位数为“渐进数”,如589就是一个“渐进数”。如果由数字3,5,6组成的三位数中随机抽取一个三位数,那么这个数是“渐进数”的概率是___.
分析 2、从-1,0, ,1,-2这五个数中,随机抽取一个数,作为函数 和关于x的方程
中p的值,恰好使得函数的图象经过第二、四象限,且方程有实数根的概率为_______.
3、现有三个自愿献血者,两人血型为O型,一人血型为A型,若三人中随意挑选一人献血,两年后又从此三人中随意挑选一人献血,试求两次所献血的血型为O型的概率。(要求:用列表或画树状图的方法解答)。练习P64 1、4小结:列表法
(1)定义:用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法.
(2)列表法的应用条件:当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.
树状图法
(1)定义:通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法.
(2)运用树状图法求概率的条件:当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.作业P64 2、3
温故知新 上节课,你学会了用什么方法求某个事件发生的概率.答:树状图、列表格.问题提出 例1 小明、小颖和小凡做“石头、剪刀、布”的游戏,游戏规则如下:
由小明和小颖玩“石头、剪刀、布”游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者.
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?解法1:因为小明和小颖每次出这三种手势的可能性相同,所以可以利用树状图列出所有可能出现的结果:石头
剪刀
布开始此颜色小凡获胜此颜色小明获胜此颜色小颖获胜所以,这个游戏对三人是公平的.总共有9种可能的结果,每种结果出现的可能性相同.由树状图可知:解法2:根据题意列表如下:由列表可知:所以,这个游戏对三人是公平的.做一做(分组讨论) 小明和小军两人一起做游戏.游戏规则如下:每人从1,2,…,12中任意选择一个数,然后两人各掷一次均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负.如果你是游戏者,你会选择哪个数?掷得点数之和是哪个数的概论最大,选择这个数后获胜的概率最大.解:根据题意,列表可得则两人各掷一次质地均匀的骰子,共有36种等可能的结果,由表格可得点数和为7的结果最多,共6种,故选择数字7.第一次第二次 有三张大小一样而画面不同的画片,先将每一张从中间剪开,分成上下两部分;然后把三张画片的上半部分都放在第一个盒子中,把下半部分都放在第二个盒子中.分别摇匀后,从每个盒子中各随机地摸出一张,求这两张恰好能拼成原来的一幅画的概率随堂练习P64解:列表格得:第一个盒子第二个盒子子∴共有9种不同的拼法
∴能拼成一幅画的概率是 .中考链接:1. 定义:百位、十位、个位上的数字从左到右依次增大的三位数为“渐进数”,如589就是一个“渐进数”。如果由数字3,5,6组成的三位数中随机抽取一个三位数,那么这个数是“渐进数”的概率是___.
分析 2、从-1,0, ,1,-2这五个数中,随机抽取一个数,作为函数 和关于x的方程
中p的值,恰好使得函数的图象经过第二、四象限,且方程有实数根的概率为_______.
3、现有三个自愿献血者,两人血型为O型,一人血型为A型,若三人中随意挑选一人献血,两年后又从此三人中随意挑选一人献血,试求两次所献血的血型为O型的概率。(要求:用列表或画树状图的方法解答)。练习P64 1、4小结:列表法
(1)定义:用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法.
(2)列表法的应用条件:当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.
树状图法
(1)定义:通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法.
(2)运用树状图法求概率的条件:当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.作业P64 2、3
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
