3.1 用树状图或表格求概率课件(第3课时)
文档属性
| 名称 | 3.1 用树状图或表格求概率课件(第3课时) |  | |
| 格式 | ppt | ||
| 文件大小 | 604.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-21 22:16:02 | ||
图片预览



文档简介
(共14张PPT)
第三章 对概率的进一步研究
3.1 用树状图或表格求概率(三)
红
白
黄
蓝
绿
A盘
B盘
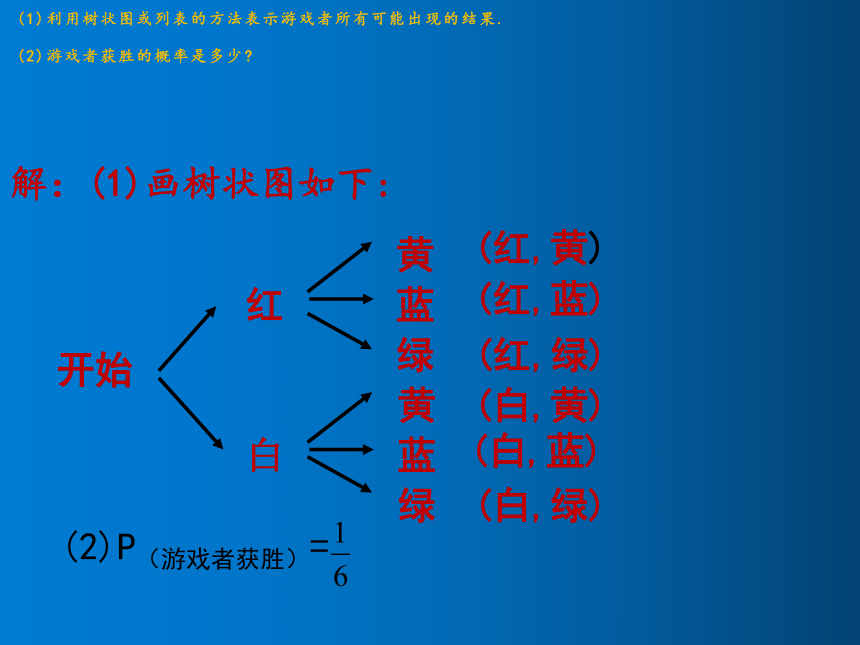
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少
解:(1)画树状图如下:
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
(2)P(游戏者获胜)=
表格可以是:
第二个
转盘
第一个
转盘
黄
蓝
绿
红
白
(红,黄)
(白,黄)
(红,蓝)
(白,蓝)
(红,绿)
(白,绿)
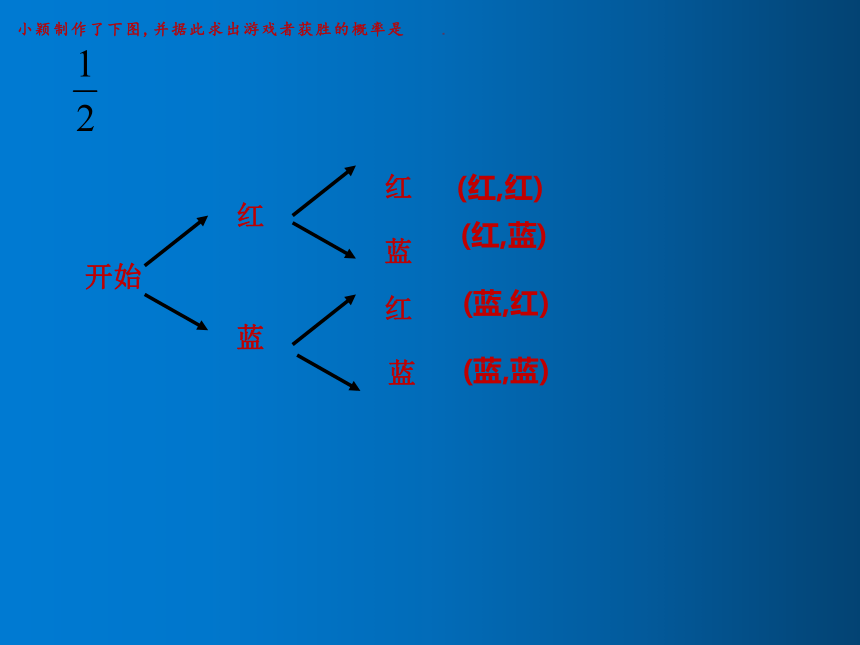
小颖制作了下图,并据此求出游戏者获胜的概率是 .
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
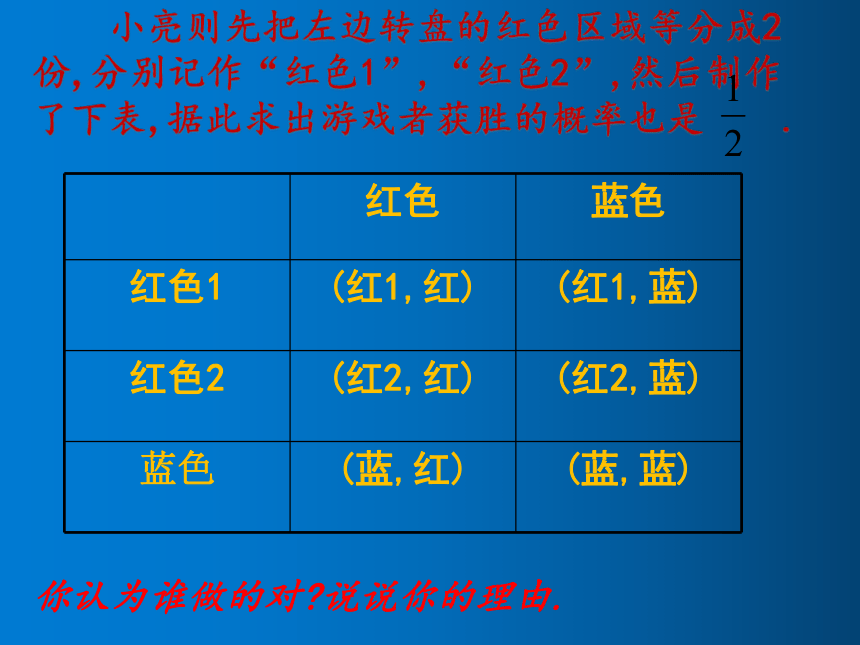
小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是 .
红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
你认为谁做的对 说说你的理由.
用树状图和列表的方法求概率时应注意些什么
议一议
各种情况出现的可能性相同
一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球。求两次摸到的球的颜色能配成紫色的概率.
例2
解:把两个红球记作“红1”、“红2”;两个白球记为“白1”、“白2”,然后列表如下:
总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种:(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),
所以P(能配成紫色)=
随堂练习
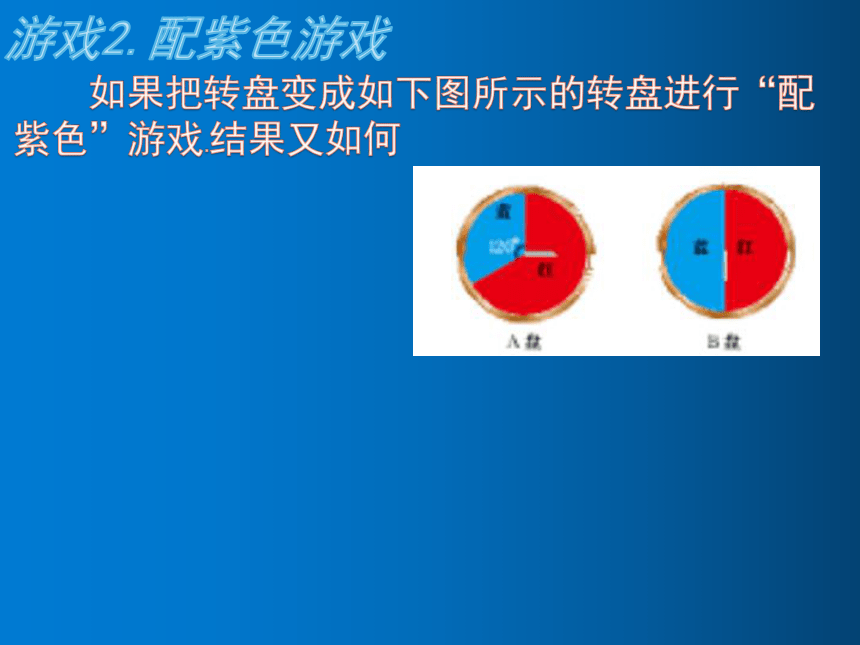
1.用如图所示的两个转盘做“配紫色”游戏,每个转盘都被分成三个面积相等的三个扇形.请求出配成紫色的概率是多少?
2.设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为 .
课堂小结
1.利用树状图和列表法求概率时应注意什么?
2.你还有哪些收获和疑惑?
习题3.3第1、2、3题
作业布置
第三章 对概率的进一步研究
3.1 用树状图或表格求概率(三)
红
白
黄
蓝
绿
A盘
B盘
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少
解:(1)画树状图如下:
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
(2)P(游戏者获胜)=
表格可以是:
第二个
转盘
第一个
转盘
黄
蓝
绿
红
白
(红,黄)
(白,黄)
(红,蓝)
(白,蓝)
(红,绿)
(白,绿)
小颖制作了下图,并据此求出游戏者获胜的概率是 .
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是 .
红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
你认为谁做的对 说说你的理由.
用树状图和列表的方法求概率时应注意些什么
议一议
各种情况出现的可能性相同
一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球。求两次摸到的球的颜色能配成紫色的概率.
例2
解:把两个红球记作“红1”、“红2”;两个白球记为“白1”、“白2”,然后列表如下:
总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种:(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),
所以P(能配成紫色)=
随堂练习
1.用如图所示的两个转盘做“配紫色”游戏,每个转盘都被分成三个面积相等的三个扇形.请求出配成紫色的概率是多少?
2.设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为 .
课堂小结
1.利用树状图和列表法求概率时应注意什么?
2.你还有哪些收获和疑惑?
习题3.3第1、2、3题
作业布置
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
