冀教版九年级数学上册同步测试卷25.4 相似三角形的判定(二)(含部分答案)
文档属性
| 名称 | 冀教版九年级数学上册同步测试卷25.4 相似三角形的判定(二)(含部分答案) |  | |
| 格式 | zip | ||
| 文件大小 | 60.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:02:38 | ||
图片预览

文档简介
《25.4
相似三角形的判定(二)》
一、选择题
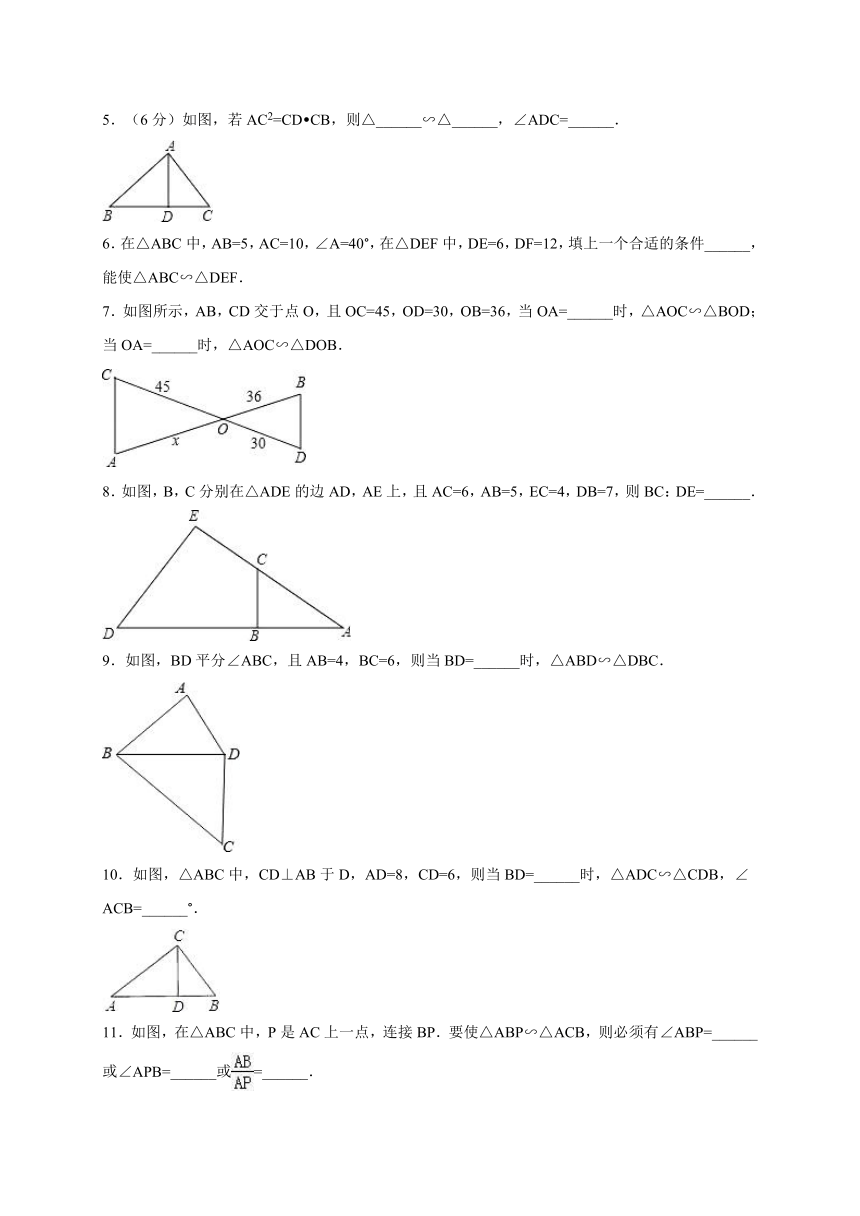
1.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似
B.①与③相似
C.①与④相似
D.②与④相似
2.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A.
B.
C.
D.
3.能判定△ABC∽△A′B′C′的条件是( )
A.
=,∠B=∠B′
B.
=,∠B=∠B′
C.
=,∠A=∠A′
D.
=,∠A=∠A′
4.如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A.
B.
C.∠B=∠D
D.∠C=∠AED
二、填空题
5.(6分)如图,若AC2=CD CB,则△______∽△______,∠ADC=______.
6.在△ABC中,AB=5,AC=10,∠A=40°,在△DEF中,DE=6,DF=12,填上一个合适的条件______,能使△ABC∽△DEF.
7.如图所示,AB,CD交于点O,且OC=45,OD=30,OB=36,当OA=______时,△AOC∽△BOD;当OA=______时,△AOC∽△DOB.
8.如图,B,C分别在△ADE的边AD,AE上,且AC=6,AB=5,EC=4,DB=7,则BC:DE=______.
9.如图,BD平分∠ABC,且AB=4,BC=6,则当BD=______时,△ABD∽△DBC.
10.如图,△ABC中,CD⊥AB于D,AD=8,CD=6,则当BD=______时,△ADC∽△CDB,∠ACB=______°.
11.如图,在△ABC中,P是AC上一点,连接BP.要使△ABP∽△ACB,则必须有∠ABP=______或∠APB=______或=______.
12.如图,在三角形ABC中,AB=24,AC=18,D是AC上一点AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=______.
13.在方格纸中,每个小格的顶点称为格点,以格点为顶点的三角形叫做格点三角形.在如图5×5的方格纸中,以A、B为顶点作格点三角形与△OAB相似(相似比不能为1),则另一个顶点C的坐标为______.
三、解答题
14.如图,判断两个三角形是否相似,并求出x和y.
15.如图,在△ABC中,∠C=90°,D、E分别为AB、AC边上的两点,且AD AB=
AE AC.求证:DE⊥AB.
16.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.
求证:△ADQ∽△QCP.
四、综合运用题
17.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动,点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒钟△PBQ与△ABC相似?
《25.4
相似三角形的判定(二)》
答案
一、选择题
1.B;2.C;3.C;4.B;
二、填空题
5.ACD;BCA;∠BAC;6.∠D=40°;7.54;37.5;8.;9.2;10.;90;11.∠C;∠ABC;;12.16或9;13.(5,2)或(4,4);
相似三角形的判定(二)》
一、选择题
1.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似
B.①与③相似
C.①与④相似
D.②与④相似
2.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A.
B.
C.
D.
3.能判定△ABC∽△A′B′C′的条件是( )
A.
=,∠B=∠B′
B.
=,∠B=∠B′
C.
=,∠A=∠A′
D.
=,∠A=∠A′
4.如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A.
B.
C.∠B=∠D
D.∠C=∠AED
二、填空题
5.(6分)如图,若AC2=CD CB,则△______∽△______,∠ADC=______.
6.在△ABC中,AB=5,AC=10,∠A=40°,在△DEF中,DE=6,DF=12,填上一个合适的条件______,能使△ABC∽△DEF.
7.如图所示,AB,CD交于点O,且OC=45,OD=30,OB=36,当OA=______时,△AOC∽△BOD;当OA=______时,△AOC∽△DOB.
8.如图,B,C分别在△ADE的边AD,AE上,且AC=6,AB=5,EC=4,DB=7,则BC:DE=______.
9.如图,BD平分∠ABC,且AB=4,BC=6,则当BD=______时,△ABD∽△DBC.
10.如图,△ABC中,CD⊥AB于D,AD=8,CD=6,则当BD=______时,△ADC∽△CDB,∠ACB=______°.
11.如图,在△ABC中,P是AC上一点,连接BP.要使△ABP∽△ACB,则必须有∠ABP=______或∠APB=______或=______.
12.如图,在三角形ABC中,AB=24,AC=18,D是AC上一点AD=12,在AB上取一点E,使A、D、E三点组成的三角形与ABC相似,则AE=______.
13.在方格纸中,每个小格的顶点称为格点,以格点为顶点的三角形叫做格点三角形.在如图5×5的方格纸中,以A、B为顶点作格点三角形与△OAB相似(相似比不能为1),则另一个顶点C的坐标为______.
三、解答题
14.如图,判断两个三角形是否相似,并求出x和y.
15.如图,在△ABC中,∠C=90°,D、E分别为AB、AC边上的两点,且AD AB=
AE AC.求证:DE⊥AB.
16.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.
求证:△ADQ∽△QCP.
四、综合运用题
17.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动,点Q从点B开始沿BC向C点以4cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒钟△PBQ与△ABC相似?
《25.4
相似三角形的判定(二)》
答案
一、选择题
1.B;2.C;3.C;4.B;
二、填空题
5.ACD;BCA;∠BAC;6.∠D=40°;7.54;37.5;8.;9.2;10.;90;11.∠C;∠ABC;;12.16或9;13.(5,2)或(4,4);
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
