苏科版八年级下册第9章9.4 矩形、菱形、正方形教学设计
文档属性
| 名称 | 苏科版八年级下册第9章9.4 矩形、菱形、正方形教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 23.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览

文档简介
9.4矩形、菱形、正方形
教学目标:
探索并证明菱形的判定定理
会用菱形的判定定理和性质定理解决问题
经历探索、猜想、证明的过程,进一步理解对猜想进行证明的必要性,使学生逐步学会分析和综合的思考方法,发展演绎推理的能力。
教学重点、难点:探索并证明菱形的判定定理
教学过程:
一、复习提问
1.菱形的定义是什么?(有一组邻边相等的平行四边形是菱形)
2.菱形的性质有哪些?
边:菱形的四条边都相等(2)角:菱形的对角相等
对角线:菱形的对角线互相垂直且平分
2.菱形的特殊性质有哪些?
(1)菱形的四条边相等
(2)菱形的对角线互相垂直
3.猜想:这两条特殊性质的逆命题是真命题吗?
(设计意图:从菱形性质的逆命题作出猜想,让学生感受性质与判定之间的内在联系)
二、探究活动
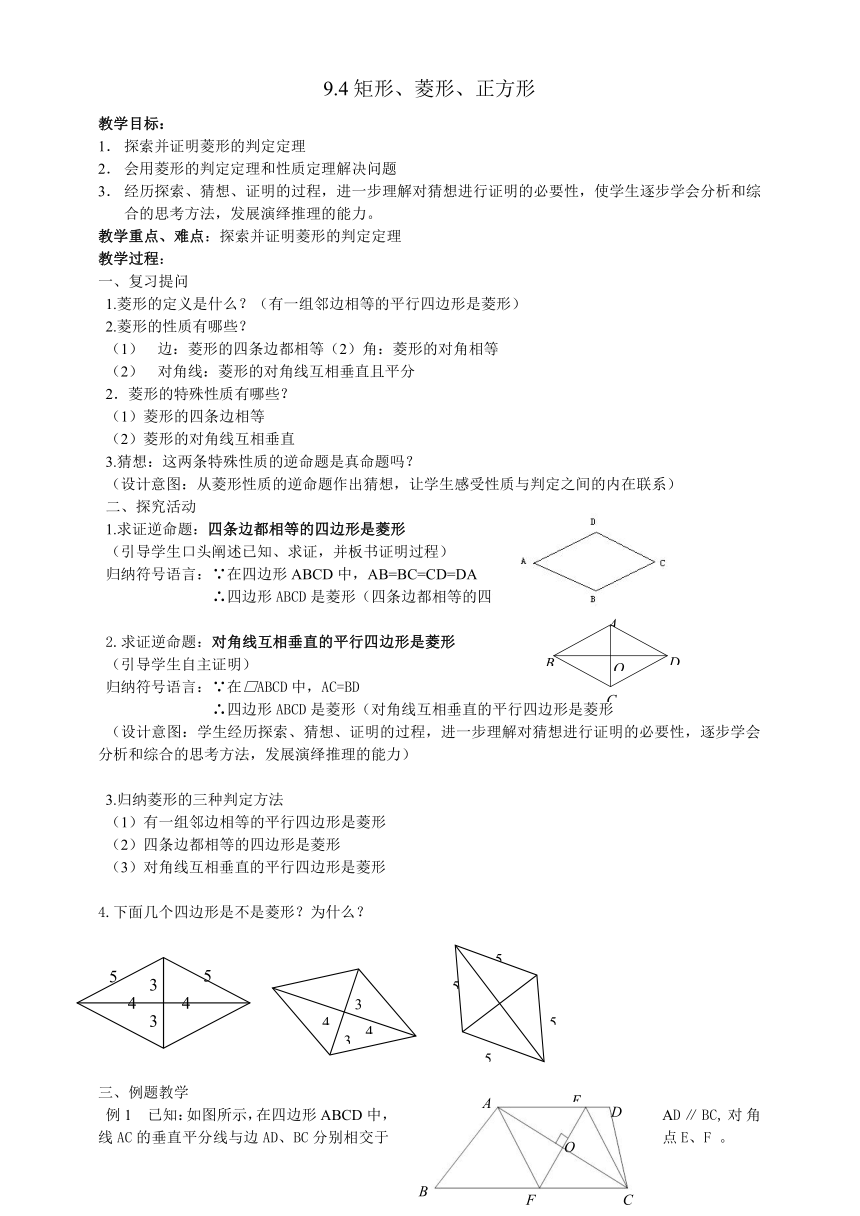
1.求证逆命题:四条边都相等的四边形是菱形
(引导学生口头阐述已知、求证,并板书证明过程)
归纳符号语言:∵在四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形(四条边都相等的四边形是菱形)
2.求证逆命题:对角线互相垂直的平行四边形是菱形
(引导学生自主证明)
归纳符号语言:∵在□ABCD中,AC=BD
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形
(设计意图:学生经历探索、猜想、证明的过程,进一步理解对猜想进行证明的必要性,逐步学会分析和综合的思考方法,发展演绎推理的能力)
3.归纳菱形的三种判定方法
(1)有一组邻边相等的平行四边形是菱形
(2)四条边都相等的四边形是菱形
(3)对角线互相垂直的平行四边形是菱形
4.下面几个四边形是不是菱形?为什么?
三、例题教学
例1
已知:如图所示,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F
。
求证:四边形AFCE是菱形
变式训练:若将“AC的垂直平分线”改为“点O是AC的中点,AE=5,AC=8,EO=3你能证明四边形AFCE是菱形吗?
(设计意图:本题鼓励学生交流,从不同角度思考,体验解决问题的多样性)
四、巩固练习
1.如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是一个菱形吗?为什么?
2.如图,E、F、G、H\分别是矩形ABCD各边的中点,四边形EFFH是怎样特殊的四边形?证明你的结论。
五、课时小结
菱形的性质和判定归纳如下表:
菱形
性质
判定
边的关系
角的关系
对角线的关系
A
B
C
D
O
5
5
4
4
3
3
3
3
4
4
5
5
5
5
A
D
B
C
E
F
O
A
B
C
D
E
F
G
H
教学目标:
探索并证明菱形的判定定理
会用菱形的判定定理和性质定理解决问题
经历探索、猜想、证明的过程,进一步理解对猜想进行证明的必要性,使学生逐步学会分析和综合的思考方法,发展演绎推理的能力。
教学重点、难点:探索并证明菱形的判定定理
教学过程:
一、复习提问
1.菱形的定义是什么?(有一组邻边相等的平行四边形是菱形)
2.菱形的性质有哪些?
边:菱形的四条边都相等(2)角:菱形的对角相等
对角线:菱形的对角线互相垂直且平分
2.菱形的特殊性质有哪些?
(1)菱形的四条边相等
(2)菱形的对角线互相垂直
3.猜想:这两条特殊性质的逆命题是真命题吗?
(设计意图:从菱形性质的逆命题作出猜想,让学生感受性质与判定之间的内在联系)
二、探究活动
1.求证逆命题:四条边都相等的四边形是菱形
(引导学生口头阐述已知、求证,并板书证明过程)
归纳符号语言:∵在四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形(四条边都相等的四边形是菱形)
2.求证逆命题:对角线互相垂直的平行四边形是菱形
(引导学生自主证明)
归纳符号语言:∵在□ABCD中,AC=BD
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形
(设计意图:学生经历探索、猜想、证明的过程,进一步理解对猜想进行证明的必要性,逐步学会分析和综合的思考方法,发展演绎推理的能力)
3.归纳菱形的三种判定方法
(1)有一组邻边相等的平行四边形是菱形
(2)四条边都相等的四边形是菱形
(3)对角线互相垂直的平行四边形是菱形
4.下面几个四边形是不是菱形?为什么?
三、例题教学
例1
已知:如图所示,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F
。
求证:四边形AFCE是菱形
变式训练:若将“AC的垂直平分线”改为“点O是AC的中点,AE=5,AC=8,EO=3你能证明四边形AFCE是菱形吗?
(设计意图:本题鼓励学生交流,从不同角度思考,体验解决问题的多样性)
四、巩固练习
1.如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是一个菱形吗?为什么?
2.如图,E、F、G、H\分别是矩形ABCD各边的中点,四边形EFFH是怎样特殊的四边形?证明你的结论。
五、课时小结
菱形的性质和判定归纳如下表:
菱形
性质
判定
边的关系
角的关系
对角线的关系
A
B
C
D
O
5
5
4
4
3
3
3
3
4
4
5
5
5
5
A
D
B
C
E
F
O
A
B
C
D
E
F
G
H
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
