九年级中考数学复习教案:函数概念、一次函数
文档属性
| 名称 | 九年级中考数学复习教案:函数概念、一次函数 |  | |
| 格式 | zip | ||
| 文件大小 | 46.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 07:04:34 | ||
图片预览

文档简介
《函数概念、一次函数》教案
一、复习目标
1、知道平面直角坐标系的相关概念,知道函数、一次函数的概念,能说出函数的三种表示方法、一次函数的性质。
2、会根据条件在平面直角坐标系中,确定点的坐标或点的位置,能画简单的一次函数图象,会用已知条件确定一次函数的关系式。
3、能比较一次函数和正比例函数的异同,体会数形结合思想,并能解决有关实际问题。
二、教学过程
1、知识回顾
让学生先完成学案上的知识回顾,让后教师进行分析。
填空
(1)在函数中,自变量x的取值范围是____________。
(2)在平面直角坐标系中,一青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2
个单位长度到Aˊ处,则Aˊ的坐标是___________。
(3)在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-2,3),B(-4,-1),C(2,0),将△ABC平移至△的位置,点A、B、C的对应点分别是、、,
若点的坐标为(3,1),则点的坐标为__________。
(4)一次函数的图象经过点(a,3),则a=____________。
2、判断下列函数关系式中哪些是一次函数(是一次函数打“√”,若不是打“×”)
(1)
(2)
(3)
(4)
(5)
(6)
3、选择
(1)点M(2,1)关于x轴对称的点的坐标(
)
A.(1,-2)
B.(-2,1)
C.(2,-1)
D.(-1,2)
(2)若一次函数的函数值y随x的增大而减小,则m的取值范围是(
)
A.M<0
B.M>0
C.M<2
D.M>2
(3)点(-2,1)在平面直角坐标系中所在的象限是(
)
A.第一象限
B.
第二象限
C.
第三象限
D.
第四象限
(4)在直线中,k<0,b>0,则直线不经过(
)
A.第一象限
B.
第二象限
C.
第三象限
D.
第四象限
(5)已知直线经过点(,3)和(1,),则的值为(
)。
A.
B.
C.
D.
设计意图:通过用小题的知识点来复习平面直角坐标系与一次函数的有关内容,让学生更容易回忆与掌握相关知识。
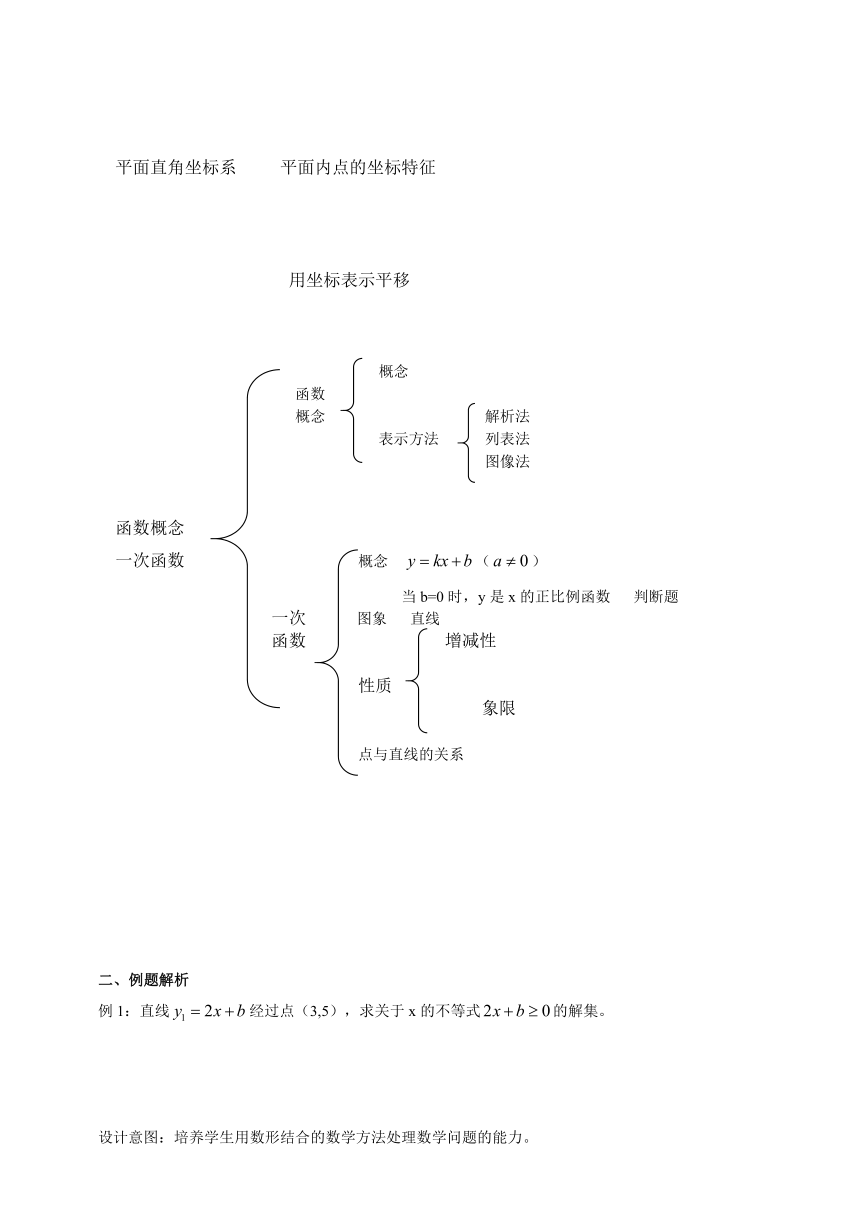
平面直角坐标系的概念
平面直角坐标系
平面内点的坐标特征
用坐标表示平移
概念
函数
概念
解析法
表示方法
列表法
图像法
函数概念
一次函数
概念
()
当b=0时,y是x的正比例函数
判断题
一次
图象
直线
函数
增减性
性质
象限
点与直线的关系
二、例题解析
例1:直线经过点(3,5),求关于x的不等式的解集。
设计意图:培养学生用数形结合的数学方法处理数学问题的能力。
例2:已知一次函数()图象过点(0,2),且与两坐标围成的三角形面积为2,求一次函数的关系式。
变式:已知分别与x轴相交于A、B两点,点C的坐标为(0,2)
在的图象上时否存在一点D,使得,求出点D的坐标;
过点C作直线CE,把的面积分成1:4两部分,求直线CE的解析式;
设计意图:培养学生用分类的数学方法处理数学问题的能力;
例3:某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式.
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
设计意图:培养学生用一次函数解决实际问题的能力和运用方程思想。
三、课堂练习
(1)一次函数y=2x-1的图象经过点(a,4),则a=__________。
(2)直线l过A、B两点,A(-1,0),B(0,1),则直线l的关系式为_____________。
(3)在平面直角坐标系xOy中,点P(2,a)在正比例函数的图象上,则Q()位于第_________象限。
(4)若一次函数的图象经过第一、二、三象限,则m的取值范围是________________。
(5)直线一定经过
(
)
A.(1,0)
B.(1,k)
C.(0,k)
D.(0,-1)
(6)下列四个点中,在正比例函数的图象上的点是
(
)
A.(2,5)
B.(5,2)
C.(2,-5)
D.(5,-1)
(7)已知一次函数的图象经过第一、二、三象限,则b的值可以是(
)
A.-2
B.-1
C.0
D.2
(8)在同一平面直角坐标系中,若一次函数与图象交于点M,则点M的坐标为(
)
A.(-1,4)
B.(-1,2)
C.(2,-1)
D.(2,1)
(9)已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是(
)
A
B
C
D
4、课堂小结
今天你的收获是什么?
5、课后作业
完成学案上剩下的练习
6、教学反思
通过本节课的学习,使学生知道平面直角坐标系的相关概念,知道函数、一次函数的概念,能说出函数的三种表示方法、一次函数的性质。通过本节课,使得学生复习并掌握了一次函数的有关知识,并使学生掌握了直接法、反例法、特殊值法、图像法、分类法、数形结合等数学方法。本节课的教学效果良好。
一、复习目标
1、知道平面直角坐标系的相关概念,知道函数、一次函数的概念,能说出函数的三种表示方法、一次函数的性质。
2、会根据条件在平面直角坐标系中,确定点的坐标或点的位置,能画简单的一次函数图象,会用已知条件确定一次函数的关系式。
3、能比较一次函数和正比例函数的异同,体会数形结合思想,并能解决有关实际问题。
二、教学过程
1、知识回顾
让学生先完成学案上的知识回顾,让后教师进行分析。
填空
(1)在函数中,自变量x的取值范围是____________。
(2)在平面直角坐标系中,一青蛙从点A(-1,0)处向右跳2个单位长度,再向上跳2
个单位长度到Aˊ处,则Aˊ的坐标是___________。
(3)在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-2,3),B(-4,-1),C(2,0),将△ABC平移至△的位置,点A、B、C的对应点分别是、、,
若点的坐标为(3,1),则点的坐标为__________。
(4)一次函数的图象经过点(a,3),则a=____________。
2、判断下列函数关系式中哪些是一次函数(是一次函数打“√”,若不是打“×”)
(1)
(2)
(3)
(4)
(5)
(6)
3、选择
(1)点M(2,1)关于x轴对称的点的坐标(
)
A.(1,-2)
B.(-2,1)
C.(2,-1)
D.(-1,2)
(2)若一次函数的函数值y随x的增大而减小,则m的取值范围是(
)
A.M<0
B.M>0
C.M<2
D.M>2
(3)点(-2,1)在平面直角坐标系中所在的象限是(
)
A.第一象限
B.
第二象限
C.
第三象限
D.
第四象限
(4)在直线中,k<0,b>0,则直线不经过(
)
A.第一象限
B.
第二象限
C.
第三象限
D.
第四象限
(5)已知直线经过点(,3)和(1,),则的值为(
)。
A.
B.
C.
D.
设计意图:通过用小题的知识点来复习平面直角坐标系与一次函数的有关内容,让学生更容易回忆与掌握相关知识。
平面直角坐标系的概念
平面直角坐标系
平面内点的坐标特征
用坐标表示平移
概念
函数
概念
解析法
表示方法
列表法
图像法
函数概念
一次函数
概念
()
当b=0时,y是x的正比例函数
判断题
一次
图象
直线
函数
增减性
性质
象限
点与直线的关系
二、例题解析
例1:直线经过点(3,5),求关于x的不等式的解集。
设计意图:培养学生用数形结合的数学方法处理数学问题的能力。
例2:已知一次函数()图象过点(0,2),且与两坐标围成的三角形面积为2,求一次函数的关系式。
变式:已知分别与x轴相交于A、B两点,点C的坐标为(0,2)
在的图象上时否存在一点D,使得,求出点D的坐标;
过点C作直线CE,把的面积分成1:4两部分,求直线CE的解析式;
设计意图:培养学生用分类的数学方法处理数学问题的能力;
例3:某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式.
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
设计意图:培养学生用一次函数解决实际问题的能力和运用方程思想。
三、课堂练习
(1)一次函数y=2x-1的图象经过点(a,4),则a=__________。
(2)直线l过A、B两点,A(-1,0),B(0,1),则直线l的关系式为_____________。
(3)在平面直角坐标系xOy中,点P(2,a)在正比例函数的图象上,则Q()位于第_________象限。
(4)若一次函数的图象经过第一、二、三象限,则m的取值范围是________________。
(5)直线一定经过
(
)
A.(1,0)
B.(1,k)
C.(0,k)
D.(0,-1)
(6)下列四个点中,在正比例函数的图象上的点是
(
)
A.(2,5)
B.(5,2)
C.(2,-5)
D.(5,-1)
(7)已知一次函数的图象经过第一、二、三象限,则b的值可以是(
)
A.-2
B.-1
C.0
D.2
(8)在同一平面直角坐标系中,若一次函数与图象交于点M,则点M的坐标为(
)
A.(-1,4)
B.(-1,2)
C.(2,-1)
D.(2,1)
(9)已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是(
)
A
B
C
D
4、课堂小结
今天你的收获是什么?
5、课后作业
完成学案上剩下的练习
6、教学反思
通过本节课的学习,使学生知道平面直角坐标系的相关概念,知道函数、一次函数的概念,能说出函数的三种表示方法、一次函数的性质。通过本节课,使得学生复习并掌握了一次函数的有关知识,并使学生掌握了直接法、反例法、特殊值法、图像法、分类法、数形结合等数学方法。本节课的教学效果良好。
同课章节目录
