人教版九年级上册第24章24.2 圆和圆的位置关系教案及反思
文档属性
| 名称 | 人教版九年级上册第24章24.2 圆和圆的位置关系教案及反思 |

|
|
| 格式 | zip | ||
| 文件大小 | 40.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览

文档简介
圆与圆的位置关系
【教学目标:】
知道圆与圆之间的五种位置关系.
经历探索两圆的位置关系与两圆半径、圆心距的数量关系间的内在联系的过程,并能运用相关结论解决有关问题.
在动手实践的过程中体会分类的思想,增强探究的意识和能力.
【教学重点、难点:】
知道圆与圆之间的五种位置关系及两圆半径、圆心距的数量关系间的内在联系
【教学过程:】
一、创设情境
导入新课
1、导入:我们已研究过点与圆、直线与圆的位置关系。
直线与圆的有几种位置关系?有几种判定方法?(板书:公共点个数、d与r的数量关系)
过渡:那么圆与圆又有怎样的位置关系呢?(板书课题)
2、操作与思考:(1)画⊙O1
(2)拿出透明纸上的⊙O2,放在同一平面内,让
⊙O2
从⊙O1的外部逐渐向⊙O1移动.
(3)在移动过程中,⊙O1与⊙O2的位置关系发生了怎样的变化?你能描述这种变化吗?
3、多媒体展示5种位置关系的图片
【设计意图:通过情境,唤醒旧知,为用类比迁移的办法研究圆与圆的位置关系作铺垫】
二、探索新知:
1、问题:你能把上述位置归类吗?你为什么这样归类?
2、归纳:
1)两圆位置关系的五种情况归纳为三类:
相离
、
相切
、
相交
.
(1)两圆相离包括外离和内含
(2)两圆相切包括外切和内切;
2)给出五种情况具体的描述性定义
(1)外离:
(2)外切:
(3)相交:
(4)内切:
(5)内含:
(同心圆是特例)
【设计意图:通过公共点的个数说明两圆的位置关系,形象直观】
3、介绍连心线(过两圆圆心的直线).问:上述图形有何特征?(轴对称图形)
4、观察并思考:两圆的切点与连心线有什么关系?
(如果两圆相切,那么切点一定在连心线上)
【反证法】假设切点不在连心线上,根据对称性,有一个点与切点对称,那么两圆有两个交点,则两圆相交,与已知相切矛盾,假设不成立.
【设计意图:介绍切点一定在连心线上,为下面研究用数量关系描述位置关系作铺垫】
介绍圆心距(两圆心之间的距离)d.
通过观察可以发现,圆心距的变化决定着圆与圆的位置关系.类比直线与圆的位置关系,我们研究d与R、r之间的数量关系描述两圆的位置关系.
(设⊙O、⊙O的半径为R、r,圆心O
、O之间的距离OO为d)
过渡:你认为哪几种比较好描述?
【设计意图:找到用数量关系区分五种位置关系的关键点:R+r,R-r】
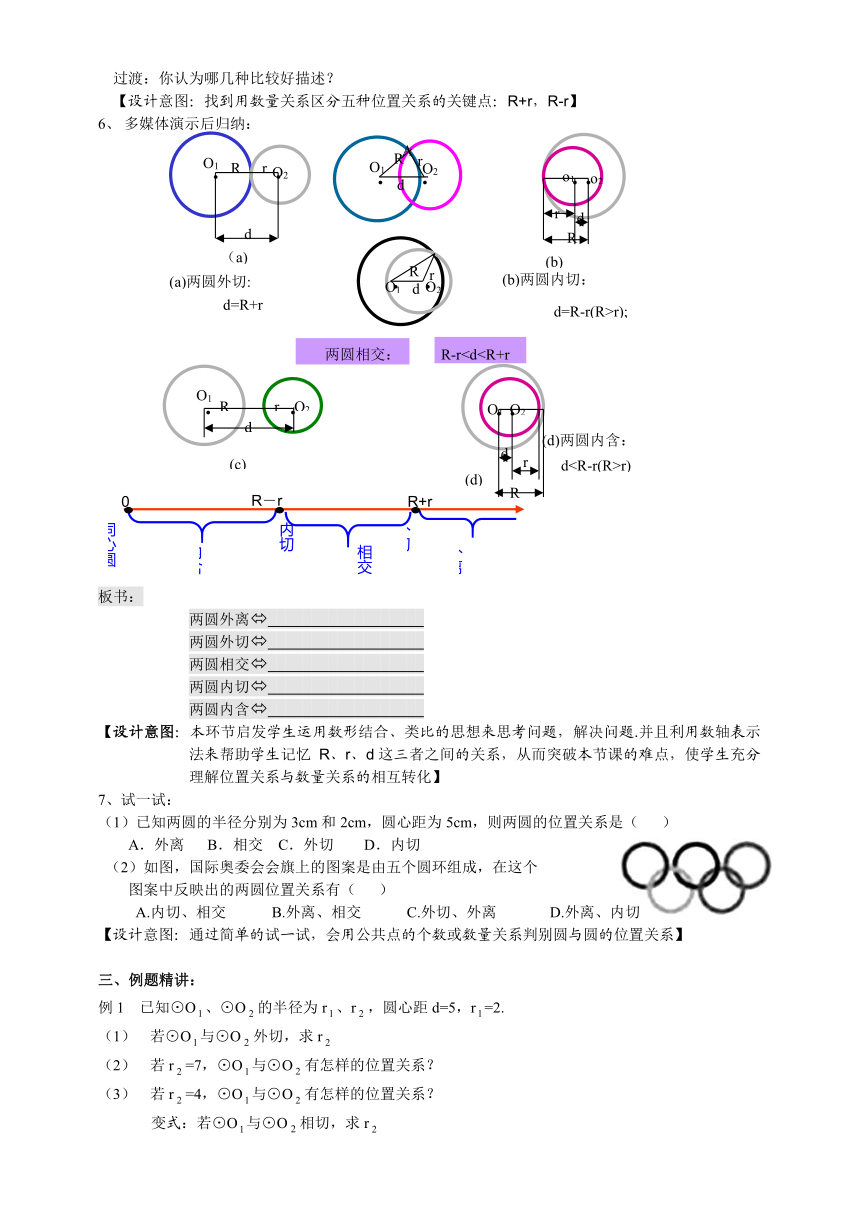
多媒体演示后归纳:
板书:
两圆外离
两圆外切
两圆相交
两圆内切
两圆内含
【设计意图:本环节启发学生运用数形结合、类比的思想来思考问题,解决问题.并且利用数轴表示法来帮助学生记忆
R、r、d这三者之间的关系,从而突破本节课的难点,使学生充分理解位置关系与数量关系的相互转化】
7、试一试:
(1)已知两圆的半径分别为3cm和2cm,圆心距为5cm,则两圆的位置关系是(
)
A.外离
B.相交
C.外切
D.内切
(2)如图,国际奥委会会旗上的图案是由五个圆环组成,在这个
图案中反映出的两圆位置关系有(
)
A.内切、相交
B.外离、相交
C.外切、外离
D.外离、内切
【设计意图:通过简单的试一试,会用公共点的个数或数量关系判别圆与圆的位置关系】
三、例题精讲:
例1
已知⊙O、⊙O的半径为r、r,圆心距d=5,r=2.
若⊙O与⊙O外切,求r
若r=7,⊙O与⊙O有怎样的位置关系?
若r=4,⊙O与⊙O有怎样的位置关系?
变式:若⊙O与⊙O相切,求r
【设计意图:本环节教师通过引导学生感受圆与圆的位置关系与数量关系的相互转化,体验转化的思想】
【练一练:】如图,⊙O的半径为5cm,点P是⊙O外一点,
OP=8cm.
以P为圆心作⊙P与⊙O相切,则⊙P的半径是
cm.
例2
已知定圆O的半径为2cm,动圆P的半径为1cm..若⊙P与⊙O相外切,那么点P与点O之间的距离是多少?点P应在怎样的图形上运动?
变式:若⊙P与⊙O相切,情况怎样?
【设计意图:通过变式训练,进一步体会相切分两种情况,继续渗透分类讨论的思想】
四、课堂小结:
1、本节课你学到的知识是:
位置关系
图形
公共点的个数
数量关系
外离
内含
相交
外切
内切
2、本节课你用到的数学思想、方法是:
【设计意图:利用图表的形式,形象的展示本节课的知识脉络,在学生脑海里形成知识体系,并且体会数学数形结合、分类讨论、转化等思想方法】
五、拓展延伸:
如图,王大伯家房屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜.他家养的一只羊平时拴在A处的一棵树上,拴羊的绳长为3m.问羊是否能吃到菜?为什么?
【设计意图:备用.数学来源于生活,又服务于生活】
【设计说明:这节课的内容与
“直线和圆的位置关系”有密切的联系,但这节课的两圆位置关系远比直线与圆的位置关系复杂.因此,准备通过复习引入和让学生动手操作,猜测两圆可能存在的位置关系,然后经过讨论,归纳确定两圆位置关系的各种情况.在与两圆位置关系相应的数量关系的研究中,鉴于学生已有直线与圆的位置关系中两量(半径、圆心到直线的距离)的数量关系的认知基础,就只运用了类比迁移的方法.这些方法的运用,都是为了充分发挥学生在探求新知过程中的主体作用.
其次,在五种位置关系相应的数量关系的研究中,我采用“先易后难,突破关键”的教学策略.先让学生解决易于解决的
“外切”、“内切”、“外离”时的三量的数量关系,再解决“内含”时的三量的数量关系,最后突破相交时三量的数量关系:R-rR+r.因此到这时,学生从两圆圆心距d的连续变化中,感悟出非负实数d的连续性.此外,我用数轴表示法来帮助学生记忆
R、r、d这三者之间的关系,突破难点.
最后,通过例题和变式训练加以巩固,总结本节内容,形成知识脉络,从始至终渗透数学的分类讨论、数形结合、转化等思想方法,提高学生的思维能力.】
【教学反思】
本课时教学内容主要探究圆与圆的位置关系和判别方法,学生通过类比、分类、数形结合,体会从不同的角度考虑事物的特点。判别圆与圆的位置关系的方法与判别直线与圆的位置的方法类似,因此本节课首先复习了直线与圆的位置关系,然后通过让学生动手操作,充分感受两圆位置的变化,猜测两圆可能存在的位置关系,经过讨论,归纳确定两圆位置关系的各种情况.通过直观感受可以得出由“公共点的个数”可以知道两圆的位置关系。在两圆位置关系相应的“数量关系”的研究中,先把课本上“读一读”的内容穿插在其中,因为只有认知了“两圆相切,切点在两圆的连心线上”,才能研究圆心到直线的距离d与两圆半径R、r的数量关系。
在五种位置关系相应的数量关系的研究中,我采用“先易后难,突破关键”的教学策略.先让学生解决易于解决的
“外切”、“内切”、“外离”时的三量的数量关系,再解决“内含”时的三量的数量关系,最后突破相交时三量的数量关系:R-rR+r.通过多媒体展示两圆圆心距d的连续变化,感悟出非负实数d的连续性.再用数轴表示法来帮助学生记忆
R、r、d这三者之间的关系,突破难点.
最后通过例题和变式练习,运用相关结论解决有关问题.
整节课以“探究过程,探究方法,探究结果,探究运用”为主线,高度重视学生的主动参与、亲自探究、动手操作,体验学习知识的过程,基本达到预期效果。上下来也有几处遗憾:
两圆相交时,圆心距与大圆半径R和小圆半径r的关系,要让学生主动发现,要让学生结合操作、完全思考后由学生自己得出结论,这样的感悟才深刻。
例题的教学虽然利用变式渗透了分类讨论的思想,也总结了一些方法教学生运用,但还不够透彻到位,学生还不够熟练。
投影和黑板的位置和灯光的原因不够清楚,版面局限,学生操作的过程没有充分展示,影响了效果。
(a)两圆外切:
d=R+r
;
(b)两圆内切:
d=R-r(R>r);
(d)两圆内含:
dr)
O1
O2
R
r
d
(a)
o1
o2
R
r
d
(b)
O1
O2
d
R
r
(c)
R
d
r
O1
(d)
O2
两圆相交:
R-rO1
O2
R
r
d
A
O1
O2
R
r
d
同心圆
内含
外离
外切
相交
内切
0
R―r
R+r
d
位
置
关
系
数
量
化
【教学目标:】
知道圆与圆之间的五种位置关系.
经历探索两圆的位置关系与两圆半径、圆心距的数量关系间的内在联系的过程,并能运用相关结论解决有关问题.
在动手实践的过程中体会分类的思想,增强探究的意识和能力.
【教学重点、难点:】
知道圆与圆之间的五种位置关系及两圆半径、圆心距的数量关系间的内在联系
【教学过程:】
一、创设情境
导入新课
1、导入:我们已研究过点与圆、直线与圆的位置关系。
直线与圆的有几种位置关系?有几种判定方法?(板书:公共点个数、d与r的数量关系)
过渡:那么圆与圆又有怎样的位置关系呢?(板书课题)
2、操作与思考:(1)画⊙O1
(2)拿出透明纸上的⊙O2,放在同一平面内,让
⊙O2
从⊙O1的外部逐渐向⊙O1移动.
(3)在移动过程中,⊙O1与⊙O2的位置关系发生了怎样的变化?你能描述这种变化吗?
3、多媒体展示5种位置关系的图片
【设计意图:通过情境,唤醒旧知,为用类比迁移的办法研究圆与圆的位置关系作铺垫】
二、探索新知:
1、问题:你能把上述位置归类吗?你为什么这样归类?
2、归纳:
1)两圆位置关系的五种情况归纳为三类:
相离
、
相切
、
相交
.
(1)两圆相离包括外离和内含
(2)两圆相切包括外切和内切;
2)给出五种情况具体的描述性定义
(1)外离:
(2)外切:
(3)相交:
(4)内切:
(5)内含:
(同心圆是特例)
【设计意图:通过公共点的个数说明两圆的位置关系,形象直观】
3、介绍连心线(过两圆圆心的直线).问:上述图形有何特征?(轴对称图形)
4、观察并思考:两圆的切点与连心线有什么关系?
(如果两圆相切,那么切点一定在连心线上)
【反证法】假设切点不在连心线上,根据对称性,有一个点与切点对称,那么两圆有两个交点,则两圆相交,与已知相切矛盾,假设不成立.
【设计意图:介绍切点一定在连心线上,为下面研究用数量关系描述位置关系作铺垫】
介绍圆心距(两圆心之间的距离)d.
通过观察可以发现,圆心距的变化决定着圆与圆的位置关系.类比直线与圆的位置关系,我们研究d与R、r之间的数量关系描述两圆的位置关系.
(设⊙O、⊙O的半径为R、r,圆心O
、O之间的距离OO为d)
过渡:你认为哪几种比较好描述?
【设计意图:找到用数量关系区分五种位置关系的关键点:R+r,R-r】
多媒体演示后归纳:
板书:
两圆外离
两圆外切
两圆相交
两圆内切
两圆内含
【设计意图:本环节启发学生运用数形结合、类比的思想来思考问题,解决问题.并且利用数轴表示法来帮助学生记忆
R、r、d这三者之间的关系,从而突破本节课的难点,使学生充分理解位置关系与数量关系的相互转化】
7、试一试:
(1)已知两圆的半径分别为3cm和2cm,圆心距为5cm,则两圆的位置关系是(
)
A.外离
B.相交
C.外切
D.内切
(2)如图,国际奥委会会旗上的图案是由五个圆环组成,在这个
图案中反映出的两圆位置关系有(
)
A.内切、相交
B.外离、相交
C.外切、外离
D.外离、内切
【设计意图:通过简单的试一试,会用公共点的个数或数量关系判别圆与圆的位置关系】
三、例题精讲:
例1
已知⊙O、⊙O的半径为r、r,圆心距d=5,r=2.
若⊙O与⊙O外切,求r
若r=7,⊙O与⊙O有怎样的位置关系?
若r=4,⊙O与⊙O有怎样的位置关系?
变式:若⊙O与⊙O相切,求r
【设计意图:本环节教师通过引导学生感受圆与圆的位置关系与数量关系的相互转化,体验转化的思想】
【练一练:】如图,⊙O的半径为5cm,点P是⊙O外一点,
OP=8cm.
以P为圆心作⊙P与⊙O相切,则⊙P的半径是
cm.
例2
已知定圆O的半径为2cm,动圆P的半径为1cm..若⊙P与⊙O相外切,那么点P与点O之间的距离是多少?点P应在怎样的图形上运动?
变式:若⊙P与⊙O相切,情况怎样?
【设计意图:通过变式训练,进一步体会相切分两种情况,继续渗透分类讨论的思想】
四、课堂小结:
1、本节课你学到的知识是:
位置关系
图形
公共点的个数
数量关系
外离
内含
相交
外切
内切
2、本节课你用到的数学思想、方法是:
【设计意图:利用图表的形式,形象的展示本节课的知识脉络,在学生脑海里形成知识体系,并且体会数学数形结合、分类讨论、转化等思想方法】
五、拓展延伸:
如图,王大伯家房屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜.他家养的一只羊平时拴在A处的一棵树上,拴羊的绳长为3m.问羊是否能吃到菜?为什么?
【设计意图:备用.数学来源于生活,又服务于生活】
【设计说明:这节课的内容与
“直线和圆的位置关系”有密切的联系,但这节课的两圆位置关系远比直线与圆的位置关系复杂.因此,准备通过复习引入和让学生动手操作,猜测两圆可能存在的位置关系,然后经过讨论,归纳确定两圆位置关系的各种情况.在与两圆位置关系相应的数量关系的研究中,鉴于学生已有直线与圆的位置关系中两量(半径、圆心到直线的距离)的数量关系的认知基础,就只运用了类比迁移的方法.这些方法的运用,都是为了充分发挥学生在探求新知过程中的主体作用.
其次,在五种位置关系相应的数量关系的研究中,我采用“先易后难,突破关键”的教学策略.先让学生解决易于解决的
“外切”、“内切”、“外离”时的三量的数量关系,再解决“内含”时的三量的数量关系,最后突破相交时三量的数量关系:R-r
R、r、d这三者之间的关系,突破难点.
最后,通过例题和变式训练加以巩固,总结本节内容,形成知识脉络,从始至终渗透数学的分类讨论、数形结合、转化等思想方法,提高学生的思维能力.】
【教学反思】
本课时教学内容主要探究圆与圆的位置关系和判别方法,学生通过类比、分类、数形结合,体会从不同的角度考虑事物的特点。判别圆与圆的位置关系的方法与判别直线与圆的位置的方法类似,因此本节课首先复习了直线与圆的位置关系,然后通过让学生动手操作,充分感受两圆位置的变化,猜测两圆可能存在的位置关系,经过讨论,归纳确定两圆位置关系的各种情况.通过直观感受可以得出由“公共点的个数”可以知道两圆的位置关系。在两圆位置关系相应的“数量关系”的研究中,先把课本上“读一读”的内容穿插在其中,因为只有认知了“两圆相切,切点在两圆的连心线上”,才能研究圆心到直线的距离d与两圆半径R、r的数量关系。
在五种位置关系相应的数量关系的研究中,我采用“先易后难,突破关键”的教学策略.先让学生解决易于解决的
“外切”、“内切”、“外离”时的三量的数量关系,再解决“内含”时的三量的数量关系,最后突破相交时三量的数量关系:R-r
R、r、d这三者之间的关系,突破难点.
最后通过例题和变式练习,运用相关结论解决有关问题.
整节课以“探究过程,探究方法,探究结果,探究运用”为主线,高度重视学生的主动参与、亲自探究、动手操作,体验学习知识的过程,基本达到预期效果。上下来也有几处遗憾:
两圆相交时,圆心距与大圆半径R和小圆半径r的关系,要让学生主动发现,要让学生结合操作、完全思考后由学生自己得出结论,这样的感悟才深刻。
例题的教学虽然利用变式渗透了分类讨论的思想,也总结了一些方法教学生运用,但还不够透彻到位,学生还不够熟练。
投影和黑板的位置和灯光的原因不够清楚,版面局限,学生操作的过程没有充分展示,影响了效果。
(a)两圆外切:
d=R+r
;
(b)两圆内切:
d=R-r(R>r);
(d)两圆内含:
d
O1
O2
R
r
d
(a)
o1
o2
R
r
d
(b)
O1
O2
d
R
r
(c)
R
d
r
O1
(d)
O2
两圆相交:
R-r
O2
R
r
d
A
O1
O2
R
r
d
同心圆
内含
外离
外切
相交
内切
0
R―r
R+r
d
位
置
关
系
数
量
化
同课章节目录
