18.1勾股定理(1)
图片预览

文档简介
2010年海南省初中数学
青年教师优质课比赛活动
教案《18.1勾股定理(1)》
文昌市华侨中学 叶丽娇
2010年4月
课题: 18.1勾 股 定 理(1)
教学目标
1、知识目标: 了解勾股定理的文化背景,体验勾股定理的探索过程及定理简单应用;
2、能力目标: 在定理的证明中培养学生的拼图能力,并通过解决问题,提高学生的运算能力、转换能力及实际应用能力;
3、情感目标: 通过对勾股定理历史的了解,感受数学文化,激发学习热情;
教学重点 探索勾股定理及定理简单应用;
教学难点 用拼图方法证明勾股定理。
教学流程安排
创设情境 活动1:欣赏图片,了解历史 探索研讨 活动2、3、4:探索勾股定理活动5:证明勾股定理 定理应用 活动5:练习1、2 小结
教学过程设计
一、创设情境,引入课题
活动1:
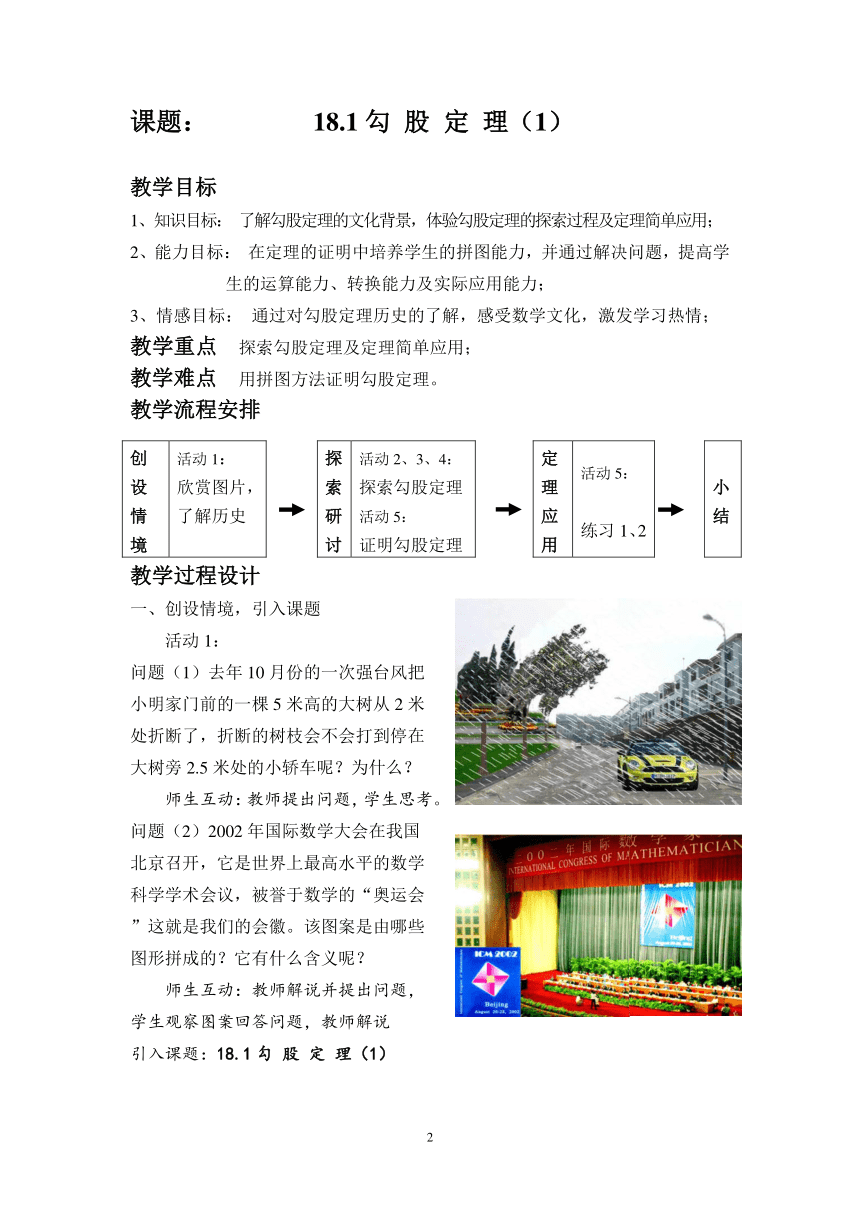
问题(1)去年10月份的一次强台风把
小明家门前的一棵5米高的大树从2米
处折断了,折断的树枝会不会打到停在
大树旁2.5米处的小轿车呢?为什么?
师生互动:教师提出问题,学生思考。
问题(2)2002年国际数学大会在我国
北京召开,它是世界上最高水平的数学
科学学术会议,被誉于数学的“奥运会
”这就是我们的会徽。该图案是由哪些
图形拼成的?它有什么含义呢?
师生互动:教师解说并提出问题,
学生观察图案回答问题,教师解说
引入课题:18.1勾 股 定 理(1)
二、探索研讨
1、探索勾股定理
活动2:
问题(3)相传2500年前,古希腊数学家毕达
哥拉斯在朋友家做客时,发现朋友家
用砖铺成的地面中反映了直角三角形
三边之间的某种数值关系
(1)我们也来观察一下你有什么发现?
(2)等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也有这样的特点
师生互动:教师解说并提出问题,引导学生观察图案,学生观察、交流、回答问题,师生共同评价,归纳结论,总结发现方法。
活动3:
类比上述方法在网格上探索两条直角边不相等的直角三角形三边的数量关系。
若网格中每一个小方格面积为1个单位面积,
那么正方形A、B、C的面积为多少?你能从中发现什么结论呢?
师生互动:教师提出问题,引导学生类比上述方法探索,学生思考、动手探索、计算回答问题,师生共同评价,归纳结论。
活动4:
同学们在网格上任意画一个直角三角形,类比上述方法探索直角三角形三边的数量关系。
师生互动:教师布置、巡视,引导,学生动手探索,得出结论。
2、同学们由以上探索,依据该图形,能否用一句话概括出以上结论呢?
命题:如果直角三角形的两条直角边分别为a和b,
斜边为c,那么
师生互动:教师提问,学生概括回答,教师板写结论。
3、证明勾股定理
活动5:
请同学们拿出我们课前准备的四个全等的直角三角形,以小组为单位,用拼图的方法验证这个命题。
师生互动:教师组织学生拼图验证结论,巡视参与并引导提示:①所拼图形面积能用直角三角形的边长来表示②所拼图形的面积要用两种不同方法表示,并用等号连结,化简验证;学生小组交流,动手拼图验证结论,小组代表展示实践结果;师生共同评价,概括归纳勾股定理。
三、应用
活动6:
练习1、如图,在在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
1 若a=12,b=5,则c等于多少?
2 若a=6,c=10,则b等于多少?
3 若b=7,c=8则a等于多少
师生互动:学生动手操作;教师巡视引导,展示学生解答结果;师生共同评价,归纳定理应用注意事项。
练习2、去年10月份的一次强台风把小明家门前的一棵5米高的大树从2米
处折断了,折断的树枝会不会打到停在大树旁2.5米处的小轿车呢?为什么?
师生互动:教师引导学生分析题意,思考,帮助学生数学建型,并提问学生用什么办法来判断?学生思考、回答、动手操作解决问题;教师巡视引导,展示学生解答结果,师生共同评价。
四、课堂小结
请同学畅所欲言谈谈本节课的收获
师生互动:教师提出问题,学生回答,教师补充共同归纳。
五、布置作业
课本P69,习题18.1第1、2题
教学板书设计
18.1勾 股 定 理(1)定理:…………………………… 练习1、……………………… …………………………… ………………………拼图验证…………………… 练习2、………………………
B
A
C
PAGE
4
青年教师优质课比赛活动
教案《18.1勾股定理(1)》
文昌市华侨中学 叶丽娇
2010年4月
课题: 18.1勾 股 定 理(1)
教学目标
1、知识目标: 了解勾股定理的文化背景,体验勾股定理的探索过程及定理简单应用;
2、能力目标: 在定理的证明中培养学生的拼图能力,并通过解决问题,提高学生的运算能力、转换能力及实际应用能力;
3、情感目标: 通过对勾股定理历史的了解,感受数学文化,激发学习热情;
教学重点 探索勾股定理及定理简单应用;
教学难点 用拼图方法证明勾股定理。
教学流程安排
创设情境 活动1:欣赏图片,了解历史 探索研讨 活动2、3、4:探索勾股定理活动5:证明勾股定理 定理应用 活动5:练习1、2 小结
教学过程设计
一、创设情境,引入课题
活动1:
问题(1)去年10月份的一次强台风把
小明家门前的一棵5米高的大树从2米
处折断了,折断的树枝会不会打到停在
大树旁2.5米处的小轿车呢?为什么?
师生互动:教师提出问题,学生思考。
问题(2)2002年国际数学大会在我国
北京召开,它是世界上最高水平的数学
科学学术会议,被誉于数学的“奥运会
”这就是我们的会徽。该图案是由哪些
图形拼成的?它有什么含义呢?
师生互动:教师解说并提出问题,
学生观察图案回答问题,教师解说
引入课题:18.1勾 股 定 理(1)
二、探索研讨
1、探索勾股定理
活动2:
问题(3)相传2500年前,古希腊数学家毕达
哥拉斯在朋友家做客时,发现朋友家
用砖铺成的地面中反映了直角三角形
三边之间的某种数值关系
(1)我们也来观察一下你有什么发现?
(2)等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也有这样的特点
师生互动:教师解说并提出问题,引导学生观察图案,学生观察、交流、回答问题,师生共同评价,归纳结论,总结发现方法。
活动3:
类比上述方法在网格上探索两条直角边不相等的直角三角形三边的数量关系。
若网格中每一个小方格面积为1个单位面积,
那么正方形A、B、C的面积为多少?你能从中发现什么结论呢?
师生互动:教师提出问题,引导学生类比上述方法探索,学生思考、动手探索、计算回答问题,师生共同评价,归纳结论。
活动4:
同学们在网格上任意画一个直角三角形,类比上述方法探索直角三角形三边的数量关系。
师生互动:教师布置、巡视,引导,学生动手探索,得出结论。
2、同学们由以上探索,依据该图形,能否用一句话概括出以上结论呢?
命题:如果直角三角形的两条直角边分别为a和b,
斜边为c,那么
师生互动:教师提问,学生概括回答,教师板写结论。
3、证明勾股定理
活动5:
请同学们拿出我们课前准备的四个全等的直角三角形,以小组为单位,用拼图的方法验证这个命题。
师生互动:教师组织学生拼图验证结论,巡视参与并引导提示:①所拼图形面积能用直角三角形的边长来表示②所拼图形的面积要用两种不同方法表示,并用等号连结,化简验证;学生小组交流,动手拼图验证结论,小组代表展示实践结果;师生共同评价,概括归纳勾股定理。
三、应用
活动6:
练习1、如图,在在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
1 若a=12,b=5,则c等于多少?
2 若a=6,c=10,则b等于多少?
3 若b=7,c=8则a等于多少
师生互动:学生动手操作;教师巡视引导,展示学生解答结果;师生共同评价,归纳定理应用注意事项。
练习2、去年10月份的一次强台风把小明家门前的一棵5米高的大树从2米
处折断了,折断的树枝会不会打到停在大树旁2.5米处的小轿车呢?为什么?
师生互动:教师引导学生分析题意,思考,帮助学生数学建型,并提问学生用什么办法来判断?学生思考、回答、动手操作解决问题;教师巡视引导,展示学生解答结果,师生共同评价。
四、课堂小结
请同学畅所欲言谈谈本节课的收获
师生互动:教师提出问题,学生回答,教师补充共同归纳。
五、布置作业
课本P69,习题18.1第1、2题
教学板书设计
18.1勾 股 定 理(1)定理:…………………………… 练习1、……………………… …………………………… ………………………拼图验证…………………… 练习2、………………………
B
A
C
PAGE
4
