华东师大版八年级数学上册12.5《因式分解》教学课件
文档属性
| 名称 | 华东师大版八年级数学上册12.5《因式分解》教学课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 07:31:09 | ||
图片预览








文档简介
课件20张PPT。12.5 因式分解平方差公式法Contents目录0102合作探究学以致用总结提升回顾思考巩固练习 (2) (3)(1)3a3b2-12ab3(4)a(x - y)2 - b(y- x)2一看系数 二看字母 三看指数关键确定公因式把下列各式分解因式:①25 x2 = (_____)2
②36a4 = (_____)2
③0.49 b2 = (_____)2
④64x2y2 = (_____)2
⑤ = (_____)25 x6a20.7 b8xy填空1)(整式乘法)(分解因式)2)1 - 9a2口算(1) 下列多项式中,他们有什么共同特征? (2)尝试将它们分别写成两个因式的乘积,并与同伴交流.① x2-25
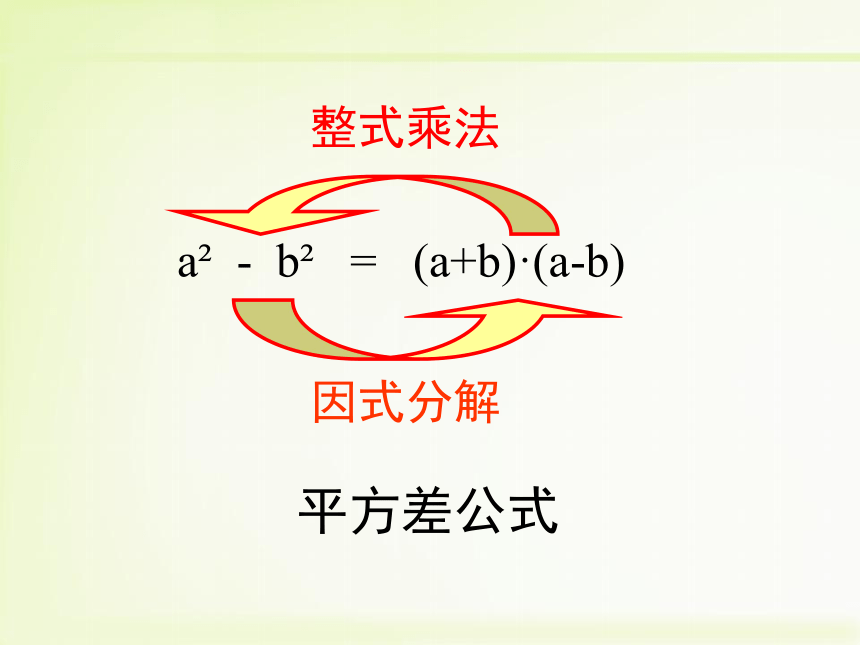
② 9x2- y2 探索交流因式分解整式乘法平方差公式a2 - b2 = (a+b)·(a-b)平方差公式(1)公式:(2)语言:
两个数的平方差,等于这两个数的和与这两个数的差的积。这个公式就是平方差公式。a2?b2= (a+b)(a?b)□2-△2=(□+△)(□-△)☆2-○2=(☆+○)(☆-○)说说平方差公式的特点两数的和与差的积两个数的平方差;只有两项 形象地表示为议一议例1、把下列各式分解因式:(1) 25 - 16x2(3) - 16x2 +81y2解(1)原式= 52-(4x)2=(5+4x)(5-4x)例2:把下列各式分解因式① 9(m+ n)2 - (m - n)2② 2x3 - 8x首先提取公因式
然后考虑用公式
最终必是连乘式解:原式=2x(x2-4)=2x(x2-22)=2x(x+2)(x-2)有公因式,哦=[3(m+n)+(m-n)][3(m+n)-(m-n)]=(3m+3n+m-n) (3m+3n-m+n)=(4m+2n) (2m+4n)=4 (2m+n) (m+2n)解:原式=[3(m+n)]2-(m-n)2① 9(m+ n)2 - (m - n)2例3、在多项式x2+y2, x2-y2 ,-x2+y2, -x2-y2中,能利用平方差公式分解的有( )
A 1个 B 2个 C 3个 D 4个B例4、判断下列分解因式是否正确
(1)(a+b)2-c2=a2+2ab+b2-c2
(2)a4-1=(a2)2-1=(a2+1)·(a2-1)想一想(1)x2+y2=(x+y)(x+y) ( )
(2)x2-y2=(x+y)(x-y) ( )
(3)-x2+y2=(-x+y)(-x-y)( )
(4)-x2 -y2 =-(x+y)(x-y) ( ) 1、判断正误2.计算(1) a2-81 (2) 36- x2
(3) 1- 16b2 (4) m2 – 9n2
(5) 0 .25q2 -121p2 (6) 169x2 -4y2
(7)9a2p2 –b2q2 (8) -16x4 +81y4 (1) a2-81
解原式=a2-92
=(a+9)(a-9)(4) m2 – 9n2
解原式=m2-(3n)2
= (m+3n)(m-3n)(3) 1-16b2
解原式=12 - (4b)2
= (1+4b)(1-4b)(2) 36- x2
解原式=62-x2
=(6+x)(6-x)(5) 0 .25q2 -121p2
解原式=(0.5q)2 - (11p)2
=(0.5q+11p)(0.5q-11p)(8) -16x4 +81y4
解原式=81y4-16x4
=(9y2)2- (4x2)2
=(9y2+4x2)(9y2-4x2)
=(9y2+4x2)〔 (3y)2-(2x)2〕
=(9y2+4x2)(3y+2x)(3y-2x)(7)9a2p2 -b2q2
解原式=(3ap)2-(bq)2 =(3ap+bq)(3ap-bq)(6) 169x2 -4y2
解原式=(13x)2-(2y)2
= (13x+2y)(13x-2y)3、如图,在一块边长为 acm 的正方形的四角,各剪去一个边长为bcm的正方形,求剩余部分的面积。如果a=3.6,b=0.8呢?a2?4b2 4.下列分解因式是否正确?为什么?如果不正确,请给出正确的结果。分解到不能再分解为止不正确 能写成( )2-( )2的式子,可以用平方差公式分解因式。 公式中的a , b可以是单独的数字、字母、单项式、多项式。 分解因式,有公因式时先“提”后“公”,应进行到每一个多项式因式不能再分解为止。
②36a4 = (_____)2
③0.49 b2 = (_____)2
④64x2y2 = (_____)2
⑤ = (_____)25 x6a20.7 b8xy填空1)(整式乘法)(分解因式)2)1 - 9a2口算(1) 下列多项式中,他们有什么共同特征? (2)尝试将它们分别写成两个因式的乘积,并与同伴交流.① x2-25
② 9x2- y2 探索交流因式分解整式乘法平方差公式a2 - b2 = (a+b)·(a-b)平方差公式(1)公式:(2)语言:
两个数的平方差,等于这两个数的和与这两个数的差的积。这个公式就是平方差公式。a2?b2= (a+b)(a?b)□2-△2=(□+△)(□-△)☆2-○2=(☆+○)(☆-○)说说平方差公式的特点两数的和与差的积两个数的平方差;只有两项 形象地表示为议一议例1、把下列各式分解因式:(1) 25 - 16x2(3) - 16x2 +81y2解(1)原式= 52-(4x)2=(5+4x)(5-4x)例2:把下列各式分解因式① 9(m+ n)2 - (m - n)2② 2x3 - 8x首先提取公因式
然后考虑用公式
最终必是连乘式解:原式=2x(x2-4)=2x(x2-22)=2x(x+2)(x-2)有公因式,哦=[3(m+n)+(m-n)][3(m+n)-(m-n)]=(3m+3n+m-n) (3m+3n-m+n)=(4m+2n) (2m+4n)=4 (2m+n) (m+2n)解:原式=[3(m+n)]2-(m-n)2① 9(m+ n)2 - (m - n)2例3、在多项式x2+y2, x2-y2 ,-x2+y2, -x2-y2中,能利用平方差公式分解的有( )
A 1个 B 2个 C 3个 D 4个B例4、判断下列分解因式是否正确
(1)(a+b)2-c2=a2+2ab+b2-c2
(2)a4-1=(a2)2-1=(a2+1)·(a2-1)想一想(1)x2+y2=(x+y)(x+y) ( )
(2)x2-y2=(x+y)(x-y) ( )
(3)-x2+y2=(-x+y)(-x-y)( )
(4)-x2 -y2 =-(x+y)(x-y) ( ) 1、判断正误2.计算(1) a2-81 (2) 36- x2
(3) 1- 16b2 (4) m2 – 9n2
(5) 0 .25q2 -121p2 (6) 169x2 -4y2
(7)9a2p2 –b2q2 (8) -16x4 +81y4 (1) a2-81
解原式=a2-92
=(a+9)(a-9)(4) m2 – 9n2
解原式=m2-(3n)2
= (m+3n)(m-3n)(3) 1-16b2
解原式=12 - (4b)2
= (1+4b)(1-4b)(2) 36- x2
解原式=62-x2
=(6+x)(6-x)(5) 0 .25q2 -121p2
解原式=(0.5q)2 - (11p)2
=(0.5q+11p)(0.5q-11p)(8) -16x4 +81y4
解原式=81y4-16x4
=(9y2)2- (4x2)2
=(9y2+4x2)(9y2-4x2)
=(9y2+4x2)〔 (3y)2-(2x)2〕
=(9y2+4x2)(3y+2x)(3y-2x)(7)9a2p2 -b2q2
解原式=(3ap)2-(bq)2 =(3ap+bq)(3ap-bq)(6) 169x2 -4y2
解原式=(13x)2-(2y)2
= (13x+2y)(13x-2y)3、如图,在一块边长为 acm 的正方形的四角,各剪去一个边长为bcm的正方形,求剩余部分的面积。如果a=3.6,b=0.8呢?a2?4b2 4.下列分解因式是否正确?为什么?如果不正确,请给出正确的结果。分解到不能再分解为止不正确 能写成( )2-( )2的式子,可以用平方差公式分解因式。 公式中的a , b可以是单独的数字、字母、单项式、多项式。 分解因式,有公因式时先“提”后“公”,应进行到每一个多项式因式不能再分解为止。
