7.2.1三角形的内角教学设计
文档属性
| 名称 | 7.2.1三角形的内角教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 43.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-07 21:12:00 | ||
图片预览

文档简介
“7.2.1三角形的内角”教学设计
琼州学院附属中学 周春媛
教学目标:
知识与技能目标:使学生掌握三角形内角和定理并能进行简单应用。
过程与方法目标:在探索三角形内角和的过程中培养学生动手、动脑的能力,并得出三角形的内角和定理,能用平行线的性质推出这一定理。
情感、态度、价值观:通过学生探索、发现等一系列的思维活动,让学生体验成功的喜悦,进而提高学生的学习兴趣。
教学重点: 三角形内角和定理。
教学难点: 三角形内角和定理的推理过程。
教学方法: 探究式教学法。
教学用具: 多媒体。
教学过程:
一、趣味引入: ∠1、∠2、∠3是一个直角三角形的三个内角,平时,它们三兄弟非常团结。可是有一天,∠2突然不高兴,发起脾气来,它指着∠1说:“你凭什么度数最大,我也要和你一样大!”“不行啊,老弟” ∠1说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么” ∠2很纳闷。同学们,你们知道其中的道理吗?学了今天的知识以后你们就会知道它们三兄弟之间的关系了……板书:7.2·1三角形的内角
[设计意图]通过故事引入,激发学生的学习兴趣。
二.动手探究
做一做
问题1:三角形的内角和等于多少?
问题2:在小学里,用什么方法得到三角形内角和的结论?
1.通过多媒体演示测量法。
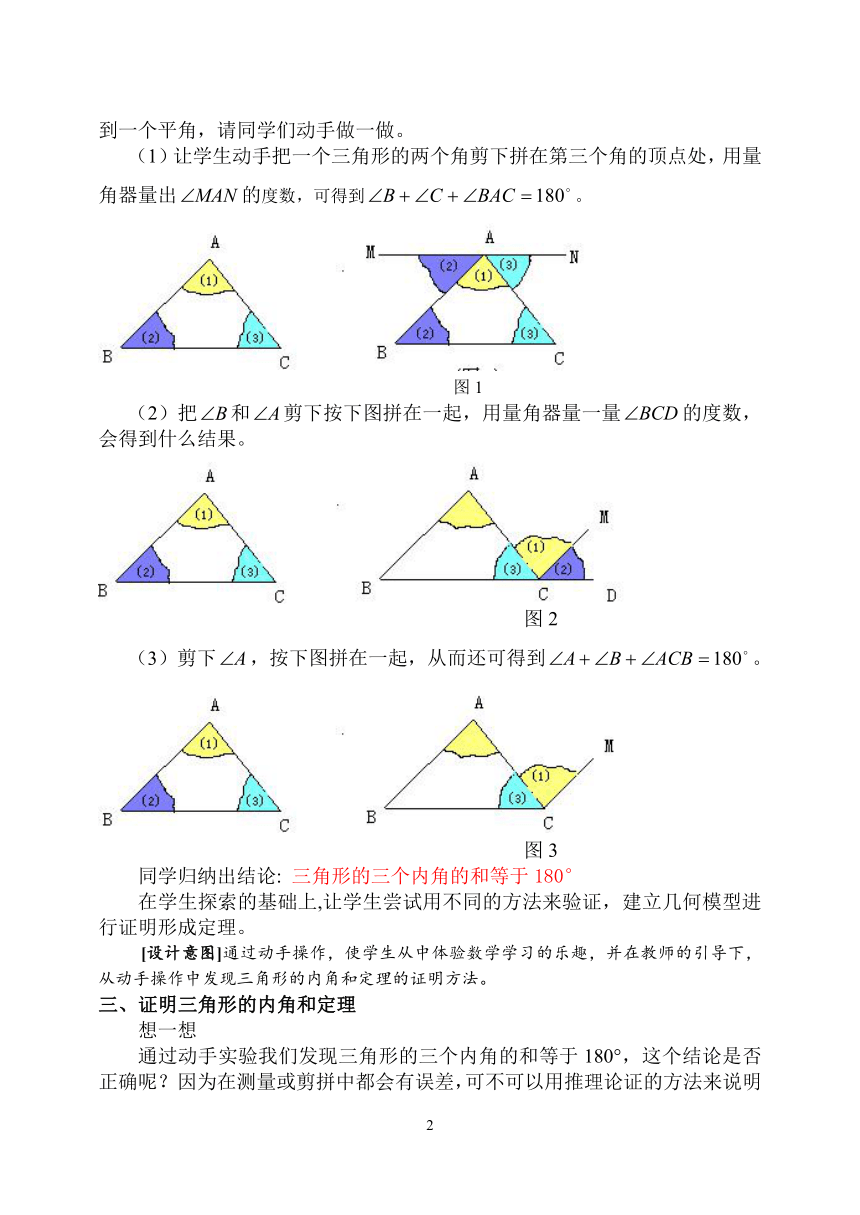
2.剪拼法:在纸上画出一个三角形,并将它的内角剪下来,拼在一起,就得到一个平角,请同学们动手做一做。
(1)让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到。
图1
(2)把和剪下按下图拼在一起,用量角器量一量的度数,会得到什么结果。
图2
(3)剪下,按下图拼在一起,从而还可得到。
图3
同学归纳出结论: 三角形的三个内角的和等于180°
在学生探索的基础上,让学生尝试用不同的方法来验证,建立几何模型进行证明形成定理。
[设计意图]通过动手操作,使学生从中体验数学学习的乐趣,并在教师的引导下,从动手操作中发现三角形的内角和定理的证明方法。
三、证明三角形的内角和定理
想一想
通过动手实验我们发现三角形的三个内角的和等于180°,这个结论是否正确呢?因为在测量或剪拼中都会有误差,可不可以用推理论证的方法来说明上面的结论的正确性呢?
根推理法的一般步骤:画图、已知、求证、证明
结合图(1)、图(2),能不能想出这个结论的证明方法呢?
已知:△ABC,求证:∠A+∠B+∠C=180°
证明:过点A作一条直线平行于BC
∵EF∥BC (已知)
∴∠1=∠B ( 两直线平行,内错角相等 )
∠2=∠C ( 两直线平行,内错角相等 )
∵∠1+∠2+∠3=180°(平角定义)
∴∠B+∠BAC+∠C=180°(等量代换)
问题:还有其它方法吗?
方法2:延长一边(如延长BC到D,作CE∥BA),利用同位角、内错角移两角,凑出平角180°(见图4)。
图4 图5
方法3:过一顶点作其对边的平行线(如过A作BC的平行线),利用内错角移角凑出平角180°(见图5)。
教师根据情况从以上方法中选用一种来进行证明,重点分析辅助线作法的目的,并板书其中一种的详细过程,得出三角形内角和定理。
[设计意图]使学生从对三角形内角和的感性认识上升到理性认识,由于学生刚刚接触证明,所以教师要有的示范,通过讲练结合,使学生逐步掌握推理的方法步骤。
四、巩固应用
1、比一比,看哪一组做又快又对。
(1)在△ABC中,∠A=,∠B=,则∠C=
(2)在△ABC中,∠C=,∠B=,则∠A=
(3)在△ABC中,∠A=,∠B=2∠A,则∠C=
2、例1,如图C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?
3、练习
1、如图,从A处观测C处时仰角∠CAD=,从B处观测C处时仰角∠CBD=.从C处观测A,B两处时视角∠ACB是多少?
[设计意图]通过例题和练习,要让学生体会三角形
内角和定理在角的求值问题中的应用,注意向学生分析解决问题的思路和方法。逐步向学生渗透数学中的思想方法,这里体现了数学中的转化思想,这一点一定要让学生体会。
五、小结
这节课你有那些收获
你学会了… …
你了解了… …
六、作业
课本P76.复习巩固:1、4.
A
B
D
C
D
B
C
A
PAGE
4
琼州学院附属中学 周春媛
教学目标:
知识与技能目标:使学生掌握三角形内角和定理并能进行简单应用。
过程与方法目标:在探索三角形内角和的过程中培养学生动手、动脑的能力,并得出三角形的内角和定理,能用平行线的性质推出这一定理。
情感、态度、价值观:通过学生探索、发现等一系列的思维活动,让学生体验成功的喜悦,进而提高学生的学习兴趣。
教学重点: 三角形内角和定理。
教学难点: 三角形内角和定理的推理过程。
教学方法: 探究式教学法。
教学用具: 多媒体。
教学过程:
一、趣味引入: ∠1、∠2、∠3是一个直角三角形的三个内角,平时,它们三兄弟非常团结。可是有一天,∠2突然不高兴,发起脾气来,它指着∠1说:“你凭什么度数最大,我也要和你一样大!”“不行啊,老弟” ∠1说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么” ∠2很纳闷。同学们,你们知道其中的道理吗?学了今天的知识以后你们就会知道它们三兄弟之间的关系了……板书:7.2·1三角形的内角
[设计意图]通过故事引入,激发学生的学习兴趣。
二.动手探究
做一做
问题1:三角形的内角和等于多少?
问题2:在小学里,用什么方法得到三角形内角和的结论?
1.通过多媒体演示测量法。
2.剪拼法:在纸上画出一个三角形,并将它的内角剪下来,拼在一起,就得到一个平角,请同学们动手做一做。
(1)让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到。
图1
(2)把和剪下按下图拼在一起,用量角器量一量的度数,会得到什么结果。
图2
(3)剪下,按下图拼在一起,从而还可得到。
图3
同学归纳出结论: 三角形的三个内角的和等于180°
在学生探索的基础上,让学生尝试用不同的方法来验证,建立几何模型进行证明形成定理。
[设计意图]通过动手操作,使学生从中体验数学学习的乐趣,并在教师的引导下,从动手操作中发现三角形的内角和定理的证明方法。
三、证明三角形的内角和定理
想一想
通过动手实验我们发现三角形的三个内角的和等于180°,这个结论是否正确呢?因为在测量或剪拼中都会有误差,可不可以用推理论证的方法来说明上面的结论的正确性呢?
根推理法的一般步骤:画图、已知、求证、证明
结合图(1)、图(2),能不能想出这个结论的证明方法呢?
已知:△ABC,求证:∠A+∠B+∠C=180°
证明:过点A作一条直线平行于BC
∵EF∥BC (已知)
∴∠1=∠B ( 两直线平行,内错角相等 )
∠2=∠C ( 两直线平行,内错角相等 )
∵∠1+∠2+∠3=180°(平角定义)
∴∠B+∠BAC+∠C=180°(等量代换)
问题:还有其它方法吗?
方法2:延长一边(如延长BC到D,作CE∥BA),利用同位角、内错角移两角,凑出平角180°(见图4)。
图4 图5
方法3:过一顶点作其对边的平行线(如过A作BC的平行线),利用内错角移角凑出平角180°(见图5)。
教师根据情况从以上方法中选用一种来进行证明,重点分析辅助线作法的目的,并板书其中一种的详细过程,得出三角形内角和定理。
[设计意图]使学生从对三角形内角和的感性认识上升到理性认识,由于学生刚刚接触证明,所以教师要有的示范,通过讲练结合,使学生逐步掌握推理的方法步骤。
四、巩固应用
1、比一比,看哪一组做又快又对。
(1)在△ABC中,∠A=,∠B=,则∠C=
(2)在△ABC中,∠C=,∠B=,则∠A=
(3)在△ABC中,∠A=,∠B=2∠A,则∠C=
2、例1,如图C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?
3、练习
1、如图,从A处观测C处时仰角∠CAD=,从B处观测C处时仰角∠CBD=.从C处观测A,B两处时视角∠ACB是多少?
[设计意图]通过例题和练习,要让学生体会三角形
内角和定理在角的求值问题中的应用,注意向学生分析解决问题的思路和方法。逐步向学生渗透数学中的思想方法,这里体现了数学中的转化思想,这一点一定要让学生体会。
五、小结
这节课你有那些收获
你学会了… …
你了解了… …
六、作业
课本P76.复习巩固:1、4.
A
B
D
C
D
B
C
A
PAGE
4
