沪科版九年级上21.2二次函数的图象和性质基础知识和同步测试题含答案
文档属性
| 名称 | 沪科版九年级上21.2二次函数的图象和性质基础知识和同步测试题含答案 | 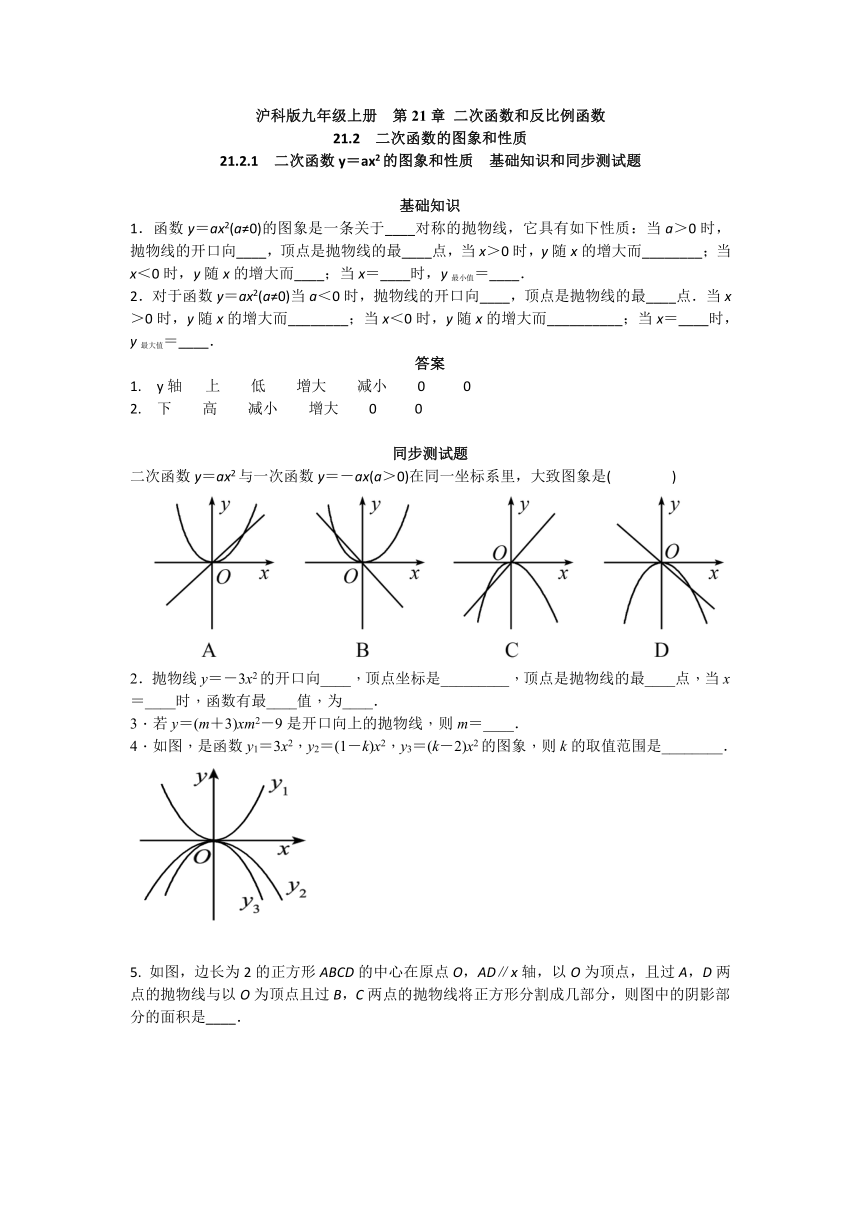 | |
| 格式 | zip | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 09:16:09 | ||
图片预览


文档简介
沪科版九年级上册
第21章
二次函数和反比例函数
21.2 二次函数的图象和性质
21.2.1 二次函数y=ax2的图象和性质
基础知识和同步测试题
基础知识
1.函数y=ax2(a≠0)的图象是一条关于____对称的抛物线,它具有如下性质:当a>0时,抛物线的开口向____,顶点是抛物线的最____点,当x>0时,y随x的增大而________;当x<0时,y随x的增大而____;当x=____时,y最小值=____.
2.对于函数y=ax2(a≠0)当a<0时,抛物线的开口向____,顶点是抛物线的最____点.当x>0时,y随x的增大而________;当x<0时,y随x的增大而__________;当x=____时,y最大值=____.
答案
1.
y轴
上
低
增大
减小
0
0
2.
下
高
减小
增大
0
0
同步测试题
二次函数y=ax2与一次函数y=-ax(a>0)在同一坐标系里,大致图象是(
)
2.抛物线y=-3x2的开口向____,顶点坐标是_________,顶点是抛物线的最____点,当x=____时,函数有最____值,为____.
3.若y=(m+3)xm2-9是开口向上的抛物线,则m=____.
4.如图,是函数y1=3x2,y2=(1-k)x2,y3=(k-2)x2的图象,则k的取值范围是________.
5.
如图,边长为2的正方形ABCD的中心在原点O,AD∥x轴,以O为顶点,且过A,D两点的抛物线与以O为顶点且过B,C两点的抛物线将正方形分割成几部分,则图中的阴影部分的面积是____.
6.已知点A(-1,y1)、点B(-,y2)、点C(-2,y3)都在函数y=-x2的图象上,则(
)
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y2>y1>y3
7.下列说法错误的是(
)
A.二次函数y=3x2中,当x>0时,y随x的增大而增大
B.二次函数y=-6x2中,当x=0时,y有最大值0
C.二次函数y=ax2图象中,开口方向与a无关
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
8.
在函数y=-x2中,当-39.函数y=(m-3)xm2-3m-2为二次函数.
(1)若其图象开口向上,求函数的关系式;
(2)若当x>0时,y随x的增大而减小,求函数的关系式.
10.给出下列函数:①y=3x;②y=-3x-1;③y=-5x2(x<0);④y=x2(x<0),其中y随x的增大而增大的函数有(
)
A.4个
B.3个
C.2个
D.1个
11.函数y=2x2,y=-3x2,y=x2的图象的共同点是(
)
A.都关于y轴对称,开口向上
B.都关于y轴对称,开口向下
C.都关于原点对称,顶点在原点
D.都关于y轴对称,顶点在原点
12.如图所示,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD的各边平行或垂直,若小正方形的边长为x,且0)
13.抛物线y=(m+1)x2上有点A(-5,2),则它的对称点B的坐标是___________.
14.二次函数y=mxm2一2有最大值,则m=____,当x____时,y随x的增大而减小.
15.如图,⊙O的半径为3,C1是函数y=x2的图象,C2是函数y=-x2的图象,则阴影部分的面积是____.
16.如图,请把图中图象的序号填在它的解析式后面.
y=2x2的图象为____.
y=x2的图象为____.
y=-x2的图象为____.
y=-x2的图象为____.
17.已知抛物线y=ax2经过点A(-2,-8).
(1)求抛物线的解析式;
(2)当x为何值时,y随x的增大而减小?
(3)当x为何值时,它有最大(小)值,是多少?
18.有一条抛物线形状的隧道,隧道的最大高度为6
m,跨度为8
m,把它放在如图所示的平面直角坐标系中.
(1)求这条抛物线所对应的函数关系式;
(2)若要在离地面4.5
m的隧道壁上,安装两盏照明灯,求两灯之间的距离.
19.
如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B,C两点,点B的坐标为(1,1).
(1)求直线AB和抛物线y=ax2的解析式;
(2)若抛物线在第一象限内有一点D,使得S△AOD=S△BOC,求点D的坐标.
答案
1.
B
2.
下
(0,0)
高
0
大
0
3.
4.
15.
2
6.
A
7.
C
8.
-99.
解:∵函数y=(m-3)xm2-3m-2为二次函数,∴m2-3m-2=2,解得m=-1或m=4 (1)∵函数图象开口向上,∴m-3>0,∴m=4,此时函数关系式为y=x2 (2)∵当x>0时,y随x的增大而减小,∴m-3<0,∴m=-1,此时函数关系式为y=-4x2
10.
C
11.
D
12.
D
13.
(5,2)
14.
-2
>0
15.
π
16
④
③
②
17.
解:(1)y=-2x2
(2)x>0 (3)x=0,y最大值=0
18.
解:(1)y=-x2
(2)设两灯为点P、点Q,则它们的纵坐标为-1.5,令-x2=-,解得x1=-2,x2=2,∴两灯间的距离PQ=4
m
第21章
二次函数和反比例函数
21.2 二次函数的图象和性质
21.2.1 二次函数y=ax2的图象和性质
基础知识和同步测试题
基础知识
1.函数y=ax2(a≠0)的图象是一条关于____对称的抛物线,它具有如下性质:当a>0时,抛物线的开口向____,顶点是抛物线的最____点,当x>0时,y随x的增大而________;当x<0时,y随x的增大而____;当x=____时,y最小值=____.
2.对于函数y=ax2(a≠0)当a<0时,抛物线的开口向____,顶点是抛物线的最____点.当x>0时,y随x的增大而________;当x<0时,y随x的增大而__________;当x=____时,y最大值=____.
答案
1.
y轴
上
低
增大
减小
0
0
2.
下
高
减小
增大
0
0
同步测试题
二次函数y=ax2与一次函数y=-ax(a>0)在同一坐标系里,大致图象是(
)
2.抛物线y=-3x2的开口向____,顶点坐标是_________,顶点是抛物线的最____点,当x=____时,函数有最____值,为____.
3.若y=(m+3)xm2-9是开口向上的抛物线,则m=____.
4.如图,是函数y1=3x2,y2=(1-k)x2,y3=(k-2)x2的图象,则k的取值范围是________.
5.
如图,边长为2的正方形ABCD的中心在原点O,AD∥x轴,以O为顶点,且过A,D两点的抛物线与以O为顶点且过B,C两点的抛物线将正方形分割成几部分,则图中的阴影部分的面积是____.
6.已知点A(-1,y1)、点B(-,y2)、点C(-2,y3)都在函数y=-x2的图象上,则(
)
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y2>y1>y3
7.下列说法错误的是(
)
A.二次函数y=3x2中,当x>0时,y随x的增大而增大
B.二次函数y=-6x2中,当x=0时,y有最大值0
C.二次函数y=ax2图象中,开口方向与a无关
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
8.
在函数y=-x2中,当-3
(1)若其图象开口向上,求函数的关系式;
(2)若当x>0时,y随x的增大而减小,求函数的关系式.
10.给出下列函数:①y=3x;②y=-3x-1;③y=-5x2(x<0);④y=x2(x<0),其中y随x的增大而增大的函数有(
)
A.4个
B.3个
C.2个
D.1个
11.函数y=2x2,y=-3x2,y=x2的图象的共同点是(
)
A.都关于y轴对称,开口向上
B.都关于y轴对称,开口向下
C.都关于原点对称,顶点在原点
D.都关于y轴对称,顶点在原点
12.如图所示,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD的各边平行或垂直,若小正方形的边长为x,且0
13.抛物线y=(m+1)x2上有点A(-5,2),则它的对称点B的坐标是___________.
14.二次函数y=mxm2一2有最大值,则m=____,当x____时,y随x的增大而减小.
15.如图,⊙O的半径为3,C1是函数y=x2的图象,C2是函数y=-x2的图象,则阴影部分的面积是____.
16.如图,请把图中图象的序号填在它的解析式后面.
y=2x2的图象为____.
y=x2的图象为____.
y=-x2的图象为____.
y=-x2的图象为____.
17.已知抛物线y=ax2经过点A(-2,-8).
(1)求抛物线的解析式;
(2)当x为何值时,y随x的增大而减小?
(3)当x为何值时,它有最大(小)值,是多少?
18.有一条抛物线形状的隧道,隧道的最大高度为6
m,跨度为8
m,把它放在如图所示的平面直角坐标系中.
(1)求这条抛物线所对应的函数关系式;
(2)若要在离地面4.5
m的隧道壁上,安装两盏照明灯,求两灯之间的距离.
19.
如图,直线AB过x轴上的一点A(2,0),且与抛物线y=ax2相交于B,C两点,点B的坐标为(1,1).
(1)求直线AB和抛物线y=ax2的解析式;
(2)若抛物线在第一象限内有一点D,使得S△AOD=S△BOC,求点D的坐标.
答案
1.
B
2.
下
(0,0)
高
0
大
0
3.
4.
1
2
6.
A
7.
C
8.
-9
解:∵函数y=(m-3)xm2-3m-2为二次函数,∴m2-3m-2=2,解得m=-1或m=4 (1)∵函数图象开口向上,∴m-3>0,∴m=4,此时函数关系式为y=x2 (2)∵当x>0时,y随x的增大而减小,∴m-3<0,∴m=-1,此时函数关系式为y=-4x2
10.
C
11.
D
12.
D
13.
(5,2)
14.
-2
>0
15.
π
16
④
③
②
17.
解:(1)y=-2x2
(2)x>0 (3)x=0,y最大值=0
18.
解:(1)y=-x2
(2)设两灯为点P、点Q,则它们的纵坐标为-1.5,令-x2=-,解得x1=-2,x2=2,∴两灯间的距离PQ=4
m
