沪科版九年级上21.1二次函数同步测试题含答案
文档属性
| 名称 | 沪科版九年级上21.1二次函数同步测试题含答案 | 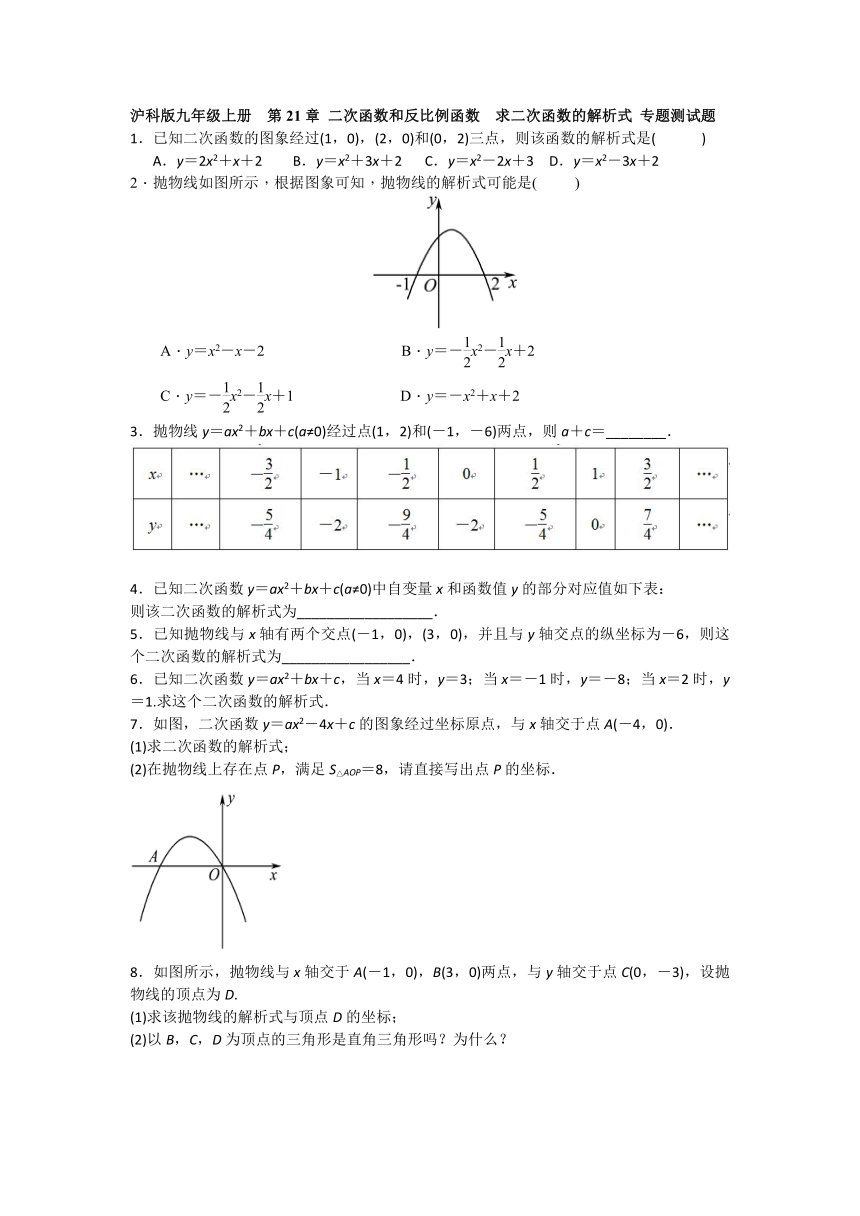 | |
| 格式 | zip | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 09:28:24 | ||
图片预览

文档简介
沪科版九年级上册
第21章
二次函数和反比例函数
求二次函数的解析式
专题测试题
1.已知二次函数的图象经过(1,0),(2,0)和(0,2)三点,则该函数的解析式是(
)
A.y=2x2+x+2
B.y=x2+3x+2
C.y=x2-2x+3
D.y=x2-3x+2
2.抛物线如图所示,根据图象可知,抛物线的解析式可能是(
)
A.y=x2-x-2
B.y=-x2-x+2
C.y=-x2-x+1
D.y=-x2+x+2
3.抛物线y=ax2+bx+c(a≠0)经过点(1,2)和(-1,-6)两点,则a+c=________.
4.已知二次函数y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:
则该二次函数的解析式为__________________.
5.已知抛物线与x轴有两个交点(-1,0),(3,0),并且与y轴交点的纵坐标为-6,则这个二次函数的解析式为_________________.
6.已知二次函数y=ax2+bx+c,当x=4时,y=3;当x=-1时,y=-8;当x=2时,y=1.求这个二次函数的解析式.
7.如图,二次函数y=ax2-4x+c的图象经过坐标原点,与x轴交于点A(-4,0).
(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
8.如图所示,抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B,C,D为顶点的三角形是直角三角形吗?为什么?
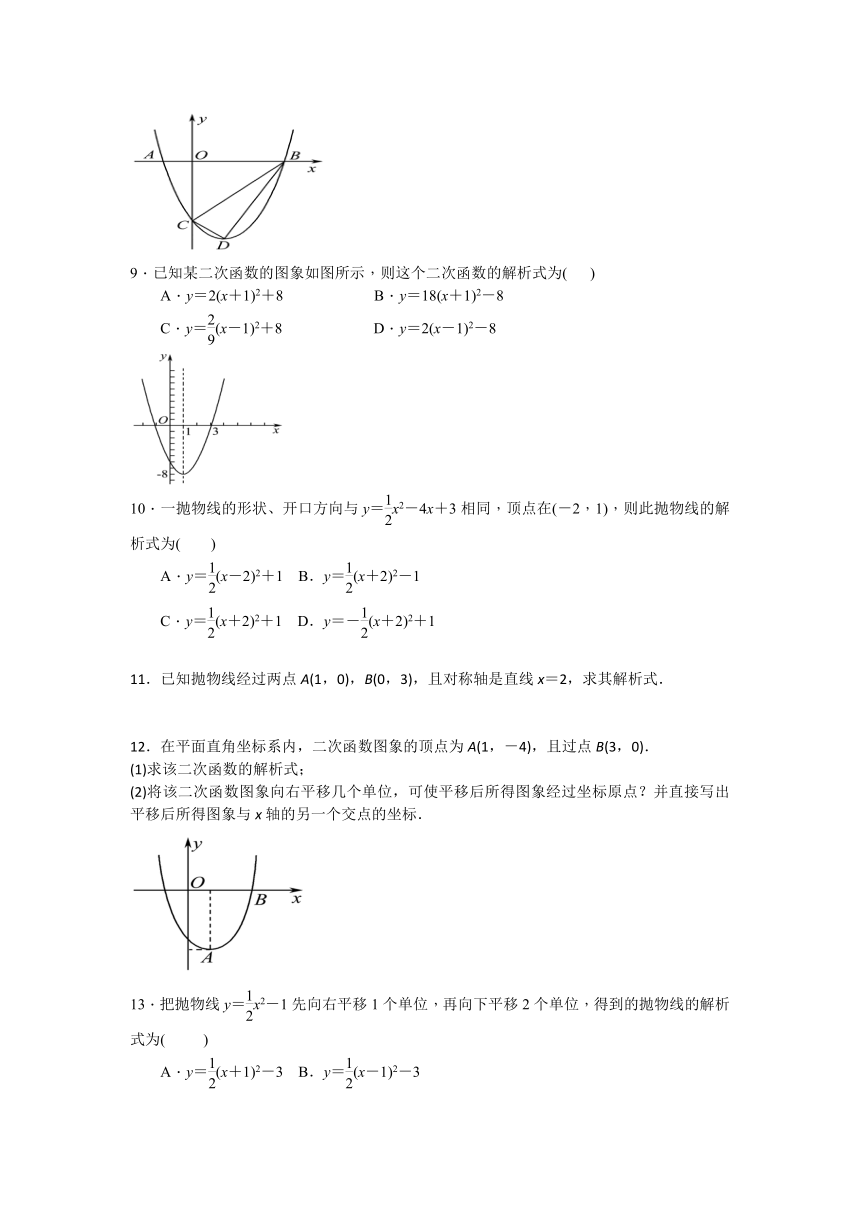
9.已知某二次函数的图象如图所示,则这个二次函数的解析式为(
)
A.y=2(x+1)2+8
B.y=18(x+1)2-8
C.y=(x-1)2+8
D.y=2(x-1)2-8
10.一抛物线的形状、开口方向与y=x2-4x+3相同,顶点在(-2,1),则此抛物线的解析式为(
)
A.y=(x-2)2+1
B.y=(x+2)2-1
C.y=(x+2)2+1
D.y=-(x+2)2+1
11.已知抛物线经过两点A(1,0),B(0,3),且对称轴是直线x=2,求其解析式.
12.在平面直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
13.把抛物线y=x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为(
)
A.y=(x+1)2-3
B.y=(x-1)2-3
C.y=(x+1)2+1
D.y=(x-1)2+1
14.如图所示,已知抛物线y=-2x2-4x的图象E,将其向右平移两个单位后得到图象F.求图象F所表示的抛物线的解析式.
15.已知二次函数y=ax2+bx-3的图象经过点A(2,3),B(-1,0).
(1)求二次函数的解析式;
(2)填空:要使二次函数的图象与x轴只有一个交点,应把图象沿y轴向上平移______个单位.
答案
1.
D
2.
D
3.
-2
4.
y=x2+x-2
5.
y=2x2-4x-6
6.
根据题意,得解得a=-,b=,c=-.∴y=-x2+x-
7.
(1)由已知条件得
解得所以,此二次函数的解析式为y=-x2-4x (2)∵点A的坐标为(-4,0),∴AO=4,设点P到x轴的距离为h,则S△AOP=×4h=8,解得h=4,①当点P在x轴上方时,-x2-4x=4,解得x=-2,所以,点P的坐标为(-2,4);②当点P在x轴下方时,-x2-4x=-4,解得x1=-2+2,x2=-2-2,所以点P的坐标为(-2+2,-4)或(-2-2,-4),综上所述,点P的坐标是(-2,4)或(-2+2,-4)或(-2-2,-4)
8.
(1)设该抛物线的解析式为y=ax2+bx+c.由抛物线与y轴交于点C(0,-3),可知c=-3,即抛物线的解析式为y=ax2+bx-3.把点A(-1,0),B(3,0)代入,得解得a=1,b=-2,∴抛物线的解析式为y=x2-2x-3.∴顶点D的坐标为(1,-4) (2)以B,C,D为顶点的三角形是直角三角形.理由如下:过点D分别作x轴,y轴的垂线,垂足分别为E,F.在Rt△BOC中,OB=3,OC=3,∴BC2=18.在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,∴CD2=2.在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,∴BD2=20.∴BC2+CD2=BD2.故△BCD为直角三角形
9.
D
10.
C
11.
依题意设抛物线的解析式为y=a(x-2)2+k,将A(1,0),B(0,3)代入得解得即抛物线的解析式为y=(x-2)2-1=x2-4x+3
12.
(1)设二次函数的解析式为y=a(x-1)2-4,∵二次函数图象过点B(3,0).∴0=4a-4,得a=1.∴二次函数的解析式为y=(x-1)2-4
(2)令y=0,得(x-1)2-4=0.解方程,得x1=3,x2=-1.∴二次函数图象与x轴的两个交点坐标分别为(3,0)和(-1,0).∴二次函数图象向右平移1个单位后所得图象经过坐标原点,平移后所得图象与x轴的另一个交点坐标为(4,0)
13.
B
14.
由平移知图象F的二次项系数为-2,y=-2x2-4x=-2(x+1)2+2,顶点坐标为(-1,2),平移后图象F的顶点坐标为(1,2),所以图象F的解析式为y=-2(x-1)2+2
15.
(1)
(1)∵二次函数y=ax2+bx-3的图象经过点A(2,3),B(-1,0),∴解得∴二次函数的解析式为y=2x2-x-3 (2)y=2x2-x-3=2(x-)2-,所以要使二次函数的图象与x轴只有一个交点,应把图象沿y轴向上平移个单位
(2)
第21章
二次函数和反比例函数
求二次函数的解析式
专题测试题
1.已知二次函数的图象经过(1,0),(2,0)和(0,2)三点,则该函数的解析式是(
)
A.y=2x2+x+2
B.y=x2+3x+2
C.y=x2-2x+3
D.y=x2-3x+2
2.抛物线如图所示,根据图象可知,抛物线的解析式可能是(
)
A.y=x2-x-2
B.y=-x2-x+2
C.y=-x2-x+1
D.y=-x2+x+2
3.抛物线y=ax2+bx+c(a≠0)经过点(1,2)和(-1,-6)两点,则a+c=________.
4.已知二次函数y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:
则该二次函数的解析式为__________________.
5.已知抛物线与x轴有两个交点(-1,0),(3,0),并且与y轴交点的纵坐标为-6,则这个二次函数的解析式为_________________.
6.已知二次函数y=ax2+bx+c,当x=4时,y=3;当x=-1时,y=-8;当x=2时,y=1.求这个二次函数的解析式.
7.如图,二次函数y=ax2-4x+c的图象经过坐标原点,与x轴交于点A(-4,0).
(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
8.如图所示,抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B,C,D为顶点的三角形是直角三角形吗?为什么?
9.已知某二次函数的图象如图所示,则这个二次函数的解析式为(
)
A.y=2(x+1)2+8
B.y=18(x+1)2-8
C.y=(x-1)2+8
D.y=2(x-1)2-8
10.一抛物线的形状、开口方向与y=x2-4x+3相同,顶点在(-2,1),则此抛物线的解析式为(
)
A.y=(x-2)2+1
B.y=(x+2)2-1
C.y=(x+2)2+1
D.y=-(x+2)2+1
11.已知抛物线经过两点A(1,0),B(0,3),且对称轴是直线x=2,求其解析式.
12.在平面直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
13.把抛物线y=x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为(
)
A.y=(x+1)2-3
B.y=(x-1)2-3
C.y=(x+1)2+1
D.y=(x-1)2+1
14.如图所示,已知抛物线y=-2x2-4x的图象E,将其向右平移两个单位后得到图象F.求图象F所表示的抛物线的解析式.
15.已知二次函数y=ax2+bx-3的图象经过点A(2,3),B(-1,0).
(1)求二次函数的解析式;
(2)填空:要使二次函数的图象与x轴只有一个交点,应把图象沿y轴向上平移______个单位.
答案
1.
D
2.
D
3.
-2
4.
y=x2+x-2
5.
y=2x2-4x-6
6.
根据题意,得解得a=-,b=,c=-.∴y=-x2+x-
7.
(1)由已知条件得
解得所以,此二次函数的解析式为y=-x2-4x (2)∵点A的坐标为(-4,0),∴AO=4,设点P到x轴的距离为h,则S△AOP=×4h=8,解得h=4,①当点P在x轴上方时,-x2-4x=4,解得x=-2,所以,点P的坐标为(-2,4);②当点P在x轴下方时,-x2-4x=-4,解得x1=-2+2,x2=-2-2,所以点P的坐标为(-2+2,-4)或(-2-2,-4),综上所述,点P的坐标是(-2,4)或(-2+2,-4)或(-2-2,-4)
8.
(1)设该抛物线的解析式为y=ax2+bx+c.由抛物线与y轴交于点C(0,-3),可知c=-3,即抛物线的解析式为y=ax2+bx-3.把点A(-1,0),B(3,0)代入,得解得a=1,b=-2,∴抛物线的解析式为y=x2-2x-3.∴顶点D的坐标为(1,-4) (2)以B,C,D为顶点的三角形是直角三角形.理由如下:过点D分别作x轴,y轴的垂线,垂足分别为E,F.在Rt△BOC中,OB=3,OC=3,∴BC2=18.在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,∴CD2=2.在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,∴BD2=20.∴BC2+CD2=BD2.故△BCD为直角三角形
9.
D
10.
C
11.
依题意设抛物线的解析式为y=a(x-2)2+k,将A(1,0),B(0,3)代入得解得即抛物线的解析式为y=(x-2)2-1=x2-4x+3
12.
(1)设二次函数的解析式为y=a(x-1)2-4,∵二次函数图象过点B(3,0).∴0=4a-4,得a=1.∴二次函数的解析式为y=(x-1)2-4
(2)令y=0,得(x-1)2-4=0.解方程,得x1=3,x2=-1.∴二次函数图象与x轴的两个交点坐标分别为(3,0)和(-1,0).∴二次函数图象向右平移1个单位后所得图象经过坐标原点,平移后所得图象与x轴的另一个交点坐标为(4,0)
13.
B
14.
由平移知图象F的二次项系数为-2,y=-2x2-4x=-2(x+1)2+2,顶点坐标为(-1,2),平移后图象F的顶点坐标为(1,2),所以图象F的解析式为y=-2(x-1)2+2
15.
(1)
(1)∵二次函数y=ax2+bx-3的图象经过点A(2,3),B(-1,0),∴解得∴二次函数的解析式为y=2x2-x-3 (2)y=2x2-x-3=2(x-)2-,所以要使二次函数的图象与x轴只有一个交点,应把图象沿y轴向上平移个单位
(2)
