苏教版高中选修3-3 3.1.1 球面的基本概念
文档属性
| 名称 | 苏教版高中选修3-3 3.1.1 球面的基本概念 |

|
|
| 格式 | zip | ||
| 文件大小 | 500.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-22 00:00:00 | ||
图片预览





文档简介
课件17张PPT。 § 3.1.1 球面的基本概念导入新课 球面是我们非常熟悉的一个曲面,在我们生活中几乎随处都有它的影子.篮球地球高尔夫球1、圆的定义类比球面的定义 圆的定义:
在一个平面内到一个定点的距离为定长的点的集合是一个圆.
定点叫做圆心,定长叫做圆的半径. 球面的定义:
在空间内到一个定点的距离为定长的点的集合
叫做球面.
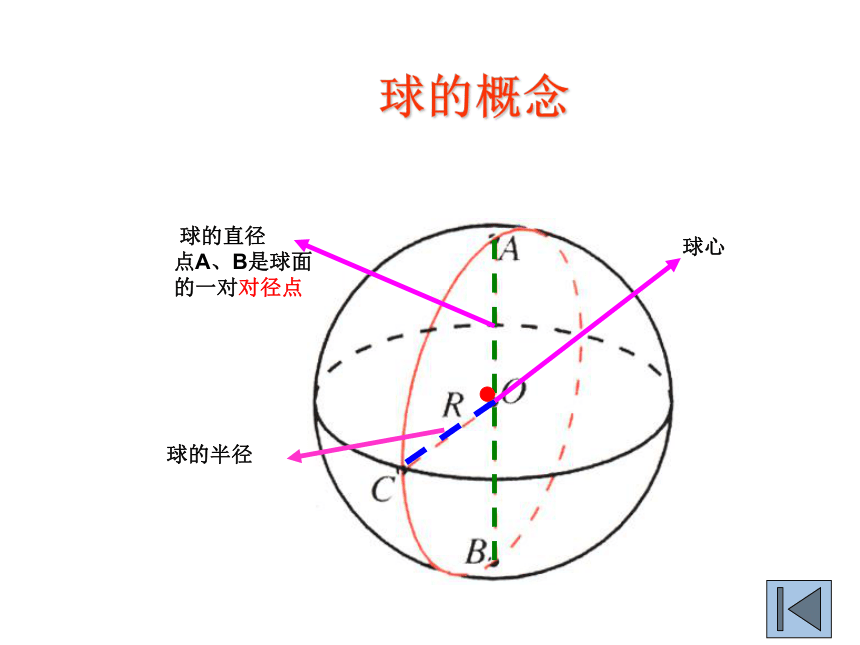
定点叫做球心,定长叫做球的半径.(如图)
球的概念2、点与圆的位置类比点与球面的位置点与圆的位置:
点在圆的内部,点在圆上,点在圆的外部.
点与球面的位置:
点在球面的内部,点在球面上,点在球面外.3、直线与圆的位置类比直线与球面的位置相离、相切、相交4、圆幂定理类比球幂定理定理1:从球面外一点P向球面引割线,
交面于Q、R两点;再从点P引球面的任
一切线,切点为S,则PS2=PQ·PR.
定理2:从球面外一点P向球面引两条
割线,它们分别与球面相交于Q、R、S、
T四点,则PQ·PR=PS·PT.
定理3:设点P是球面内一点,过点P作
两条直线,分别与球面相交于Q、R、S、
T四点,则PQ·PS=PS·PT.
定理1、2、3统称为球幂定理。 设α是一个平面,球面O的半径为R,从球心O向平面α作垂线,垂足是P,线段OP的长d就是球心O到平面α的距离.平面α与球面的关系由d决定,可以分如下几种情况: (1)d=0时,如图,平面α过球心O,这时平面α与球面交于一个与球半径一样大的圆,截面圆最大,这样的圆叫做球面上的大圆(great circle).
平面与球面的位置关系O大圆α(2) 0即 ,这样的圆叫做球面上的小圆(small circle).(3)d=R时,如图,平面α与球面O有且只有一个交点,此时平面与球面相切,惟一的交点P是切点,进一步,我们把过P的平面上的直线都叫做球面在点P处的切线(tangent line),α是P处的切平面(tangent plane).OPRα(4)d>R时,平面α与球面O没有公共点,它们不相交,自然也不相切.例题:已知球的两个平行截面的面积分别是5π和8π,它们位于球心的同一侧且相距 1,求这个球的半径。[解]如图,O1A、O2B分别是小圆半径,所以 = , =2 ,又
OO1、OO2=分别是球心到截面的距离,且O1O2=1,所以
解得R=3,即球的半径为3。O1AO2B课堂练习判断正误:(对的打√,错的打×.)
(1)在空间,到定点的距离等于定长的所有点的集合叫球.( × )
(2)球的小圆的圆心与球心的连线垂直于这个小圆所在平面.( √ )
(3)球半径是5,截面圆半径为3,则球心到截面圆所在平面的距离为4. ( √ )
谢谢指导!
在一个平面内到一个定点的距离为定长的点的集合是一个圆.
定点叫做圆心,定长叫做圆的半径. 球面的定义:
在空间内到一个定点的距离为定长的点的集合
叫做球面.
定点叫做球心,定长叫做球的半径.(如图)
球的概念2、点与圆的位置类比点与球面的位置点与圆的位置:
点在圆的内部,点在圆上,点在圆的外部.
点与球面的位置:
点在球面的内部,点在球面上,点在球面外.3、直线与圆的位置类比直线与球面的位置相离、相切、相交4、圆幂定理类比球幂定理定理1:从球面外一点P向球面引割线,
交面于Q、R两点;再从点P引球面的任
一切线,切点为S,则PS2=PQ·PR.
定理2:从球面外一点P向球面引两条
割线,它们分别与球面相交于Q、R、S、
T四点,则PQ·PR=PS·PT.
定理3:设点P是球面内一点,过点P作
两条直线,分别与球面相交于Q、R、S、
T四点,则PQ·PS=PS·PT.
定理1、2、3统称为球幂定理。 设α是一个平面,球面O的半径为R,从球心O向平面α作垂线,垂足是P,线段OP的长d就是球心O到平面α的距离.平面α与球面的关系由d决定,可以分如下几种情况: (1)d=0时,如图,平面α过球心O,这时平面α与球面交于一个与球半径一样大的圆,截面圆最大,这样的圆叫做球面上的大圆(great circle).
平面与球面的位置关系O大圆α(2) 0
OO1、OO2=分别是球心到截面的距离,且O1O2=1,所以
解得R=3,即球的半径为3。O1AO2B课堂练习判断正误:(对的打√,错的打×.)
(1)在空间,到定点的距离等于定长的所有点的集合叫球.( × )
(2)球的小圆的圆心与球心的连线垂直于这个小圆所在平面.( √ )
(3)球半径是5,截面圆半径为3,则球心到截面圆所在平面的距离为4. ( √ )
谢谢指导!
同课章节目录
