中心对称的概念和性质
图片预览



文档简介
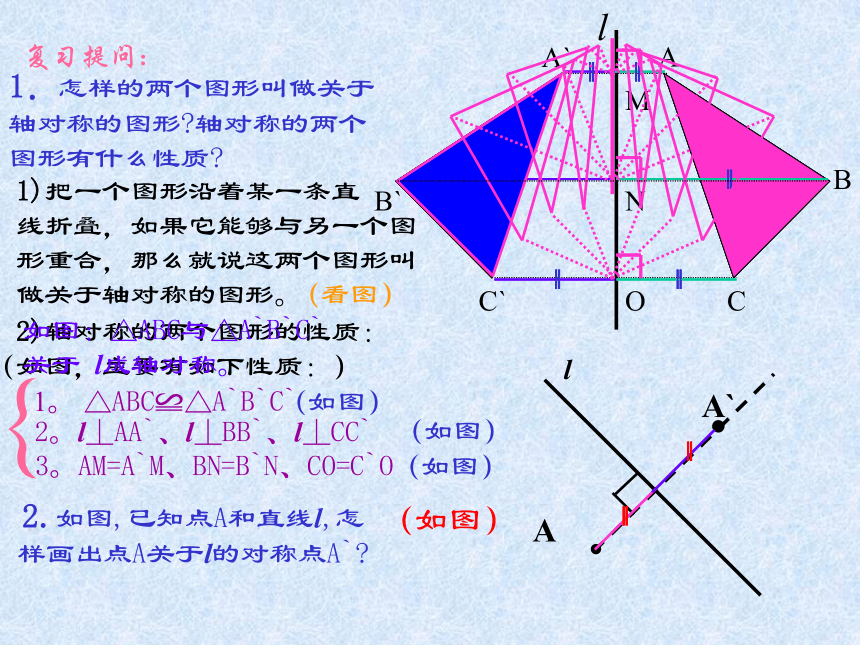
课件19张PPT。中心对称概念和性质复习提问:1.怎样的两个图形叫做关于轴对称的图形?轴对称的两个图形有什么性质?2.如图,已知点A和直线l,怎样画出点A关于l的对称点A`?(如图)ABCA`C`B`1)把一个图形沿着某一条直
线折叠,如果它能够与另一个图形重合,那么就说这两个图形叫做关于轴对称的图形。 2)轴对称的两个图形的性质:
(如图,主要有如下性质:)1。 △ABC≌△A`B`C`2。l⊥AA`、l⊥BB`、l⊥CC`MNO3。AM=A`M、BN=B`N、CO=C`O{(如图)(如图)(如图)如图:△ABC与△A`B`C`
关于 l成轴对称。l(看图) 两个图形关于点对称也
称中心对称。这两个图形中
的对应点叫做关于中心的对称点。 如图:对应点A和A`、B和B`、C和C`是关于中心O的对称点。 如图,△ABC与△A`B`C`
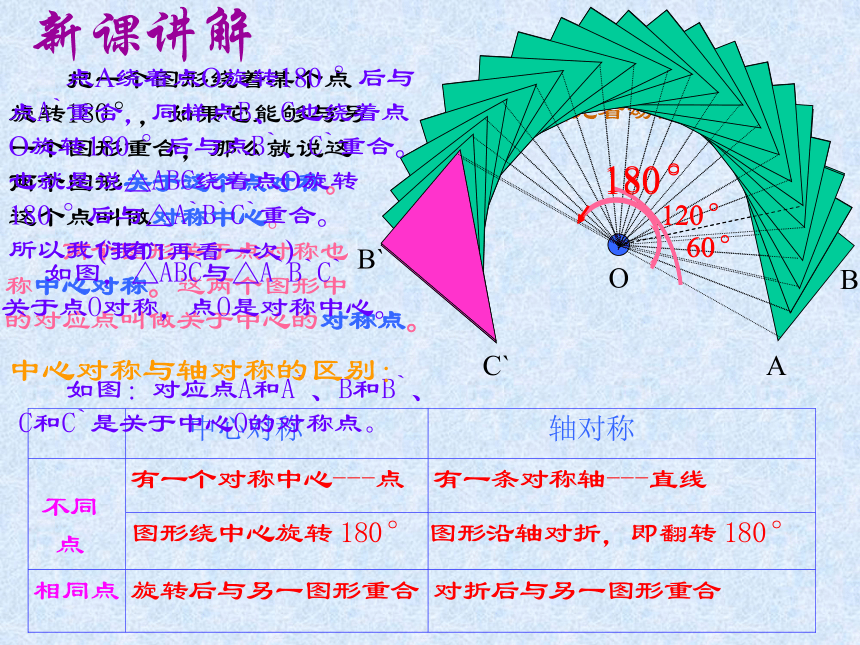
关于点O对称,点O是对称中心。中心对称与轴对称的区别:ABC新课讲解(先看动画) 把一个图形绕着某个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称。这个点叫做对称中心。B`A`OC`(我们再看一次) 并且由图知OA
=OA`,同理有OB=OB`,OC=OC`。
由此得到下面结论: 定理2 关于中心对
称的两个图形,对称点的
连线都经过对称中心,并
且被对称中心平分。 △ABC与△A`B`C`关于点
O成中心对称,点A、A`,B、B`
,C、C`都分别和对称中心O在
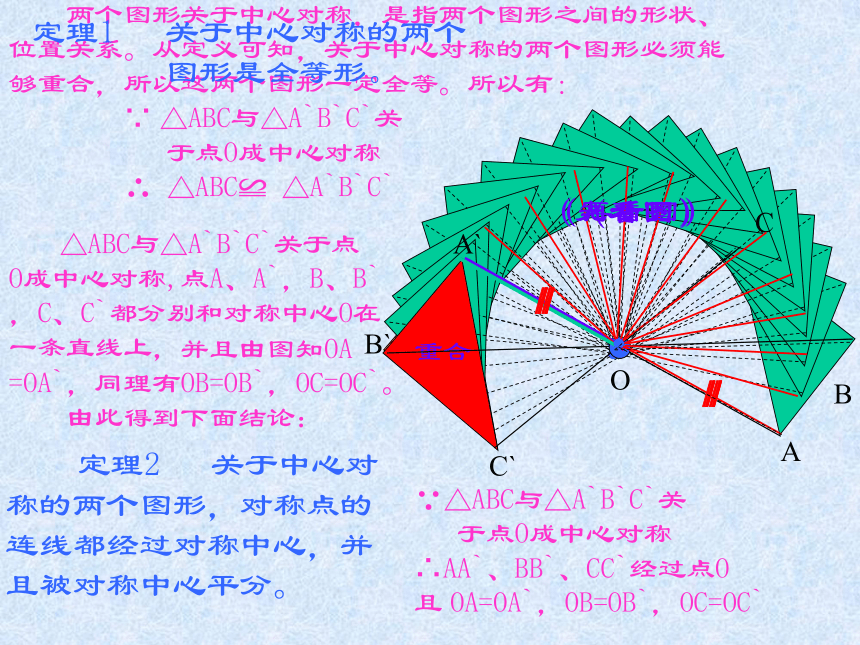
一条直线上, 两个图形关于中心对称,是指两个图形之间的形状、
位置关系。从定义可知,关于中心对称的两个图形必须能
够重合,所以这两个图形一定全等。所以有:定理1 关于中心对称的两个
图形是全等形。ABCC`B`A`O∵ △ABC与△A`B`C`关
于点O成中心对称
∴ △ABC≌ △A`B`C`∵△ABC与△A`B`C`关
于点O成中心对称
∴AA`、BB`、CC`经过点O
且 OA=OA`,OB=OB`,OC=OC`(看图)(再看图) 由已知条件,如果把其中一个图形绕着这个点
旋转180°,它必须与另一个图形重合,根据中心对
称的定义,可知这两个图形关于这一点对称。 逆定理 如果两个图形的对
应点连线都经过某一点,并且被这
一点平分,那么这两个图形关于这
一点对称。 定理2 关于中心对称的两个图形,对称点的连线都经过对称中心,并且被对称中心平分。②结论是什么?②(对称点的连线都经过对称中心,
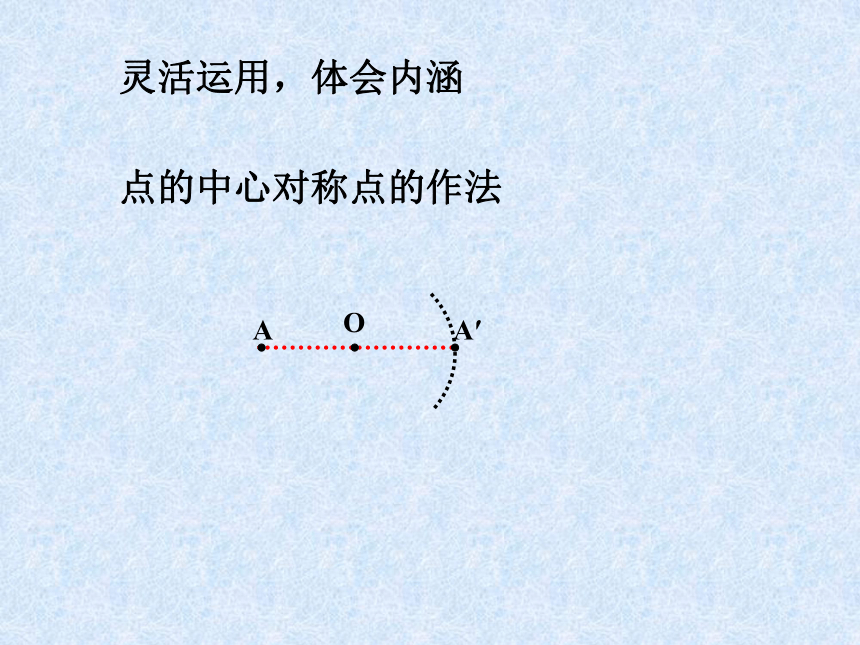
并且被对称中心平分)③它的逆命题是什么?③(如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。)(2)我们如何证明这个逆命题是正确的?定理2的逆命题作为:①(两个图形成中心对称)现在我们来研究定理2的逆命题,先看定理2。命题的已知条件(看图)命题的结论是两个图形关于这点对称(看图)AOA′ 灵活运用,体会内涵
点的中心对称点的作法AA′B′BO 线段的中心对称线段的作法例题 已知四边形ABCD和点O(如图),画四边形
A`B`C`D`,使它与已知四边形关于点O对称。ABCDO分析:要画四边形ABCD关
于点O的对称图形,只要画
A、B、C、D四点关于点O
的对称点。再顺次连接各点
即可。画法:1。连接AO并延长到A`,使
OA=OA`,得到点A的对称点A`。2。同样画B、C、D的对称点B`、
C`、D`。3。顺次连接A`、B`、C`、D`各点。∴四边形A`B`C`D`就是
所求的四边形。A′B′C ′1. 如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.练 习O[例4] 如图,已知△ABC与△A’B’C’中心对称,
求出它们的对称中心O。O[例4] 如图,已知△ABC与△A’B’C’中心对称,
求出它们的对称中心O。判断下列两个图形是否成中心对称(1)(2)(3)(4)想一想:2。判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形
不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是全等形。但全等的两个
图形不一定是成中心对称的图形。 ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴
对称的图形。 ( ) 3。选择题:
如果两个图形成中心对称,下列说法正确的是 ( )
(1)对称点连线必经过对称中心,且被对称中心平分。
(2)这两个图形一定是全等形。
(3)把一个图形绕着对称中心旋转后定与另一个图形重合。
(A)(1)(2)(3)(B)(2)(3)
(C)(1)(3) (D)(1)(2)D基础练习(一)画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。DABC∴四边形AEFG为(1)所求作。∴四边形BCMN为(2)所求作。提高练习 两个人轮流在桌子上摆放硬币.规则是每人每次摆一个在桌面上,摆好之后不许移动.不允许任何两枚硬币有重叠部分,这样经过多次摆放,规定谁放下最后一枚,并使得对方没有再放的位置,就算是谁获胜。
按照这个规则你用什么方法才能取胜呢?需要智慧的游戏分析:设想桌面很小,仅与硬币同样大小,这时显然是先放者一定获胜。再设想桌面直径仅为硬币直径的2倍,这时,先放者为了获胜,肯定不会将硬币放的挨上圆桌边缘,只要他让硬币压上桌面中心,就使对方无法再放了。看来,桌面中心是个举足轻重的位置,值得认真对待,对于一般圆桌,设想甲先置一枚硬币于圆桌中心,待乙方置一枚硬币于桌面上A处后,甲再往A处,A处关于中心的对称位置放置一枚,这样轮流下去,只要乙有位置放,甲就也有。
解:先放者获胜,操作办法是,第一枚硬币要放在桌面中心处,然后每次都往对方所放位置关于
桌面中心的对称处放。 你要争取先放,并把第1枚硬币放在桌面的对称中心上,以后你应该根据对方所放硬币的位置,在它关于中心对称的位置上放下一枚同样大小硬币.这样,由于对称性,只要对方能放得下一枚硬币,你就保证能在其对称位置上放下一枚同样大小的硬币,因此,失败绝对轮不到你. 分析:
线折叠,如果它能够与另一个图形重合,那么就说这两个图形叫做关于轴对称的图形。 2)轴对称的两个图形的性质:
(如图,主要有如下性质:)1。 △ABC≌△A`B`C`2。l⊥AA`、l⊥BB`、l⊥CC`MNO3。AM=A`M、BN=B`N、CO=C`O{(如图)(如图)(如图)如图:△ABC与△A`B`C`
关于 l成轴对称。l(看图) 两个图形关于点对称也
称中心对称。这两个图形中
的对应点叫做关于中心的对称点。 如图:对应点A和A`、B和B`、C和C`是关于中心O的对称点。 如图,△ABC与△A`B`C`
关于点O对称,点O是对称中心。中心对称与轴对称的区别:ABC新课讲解(先看动画) 把一个图形绕着某个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称。这个点叫做对称中心。B`A`OC`(我们再看一次) 并且由图知OA
=OA`,同理有OB=OB`,OC=OC`。
由此得到下面结论: 定理2 关于中心对
称的两个图形,对称点的
连线都经过对称中心,并
且被对称中心平分。 △ABC与△A`B`C`关于点
O成中心对称,点A、A`,B、B`
,C、C`都分别和对称中心O在
一条直线上, 两个图形关于中心对称,是指两个图形之间的形状、
位置关系。从定义可知,关于中心对称的两个图形必须能
够重合,所以这两个图形一定全等。所以有:定理1 关于中心对称的两个
图形是全等形。ABCC`B`A`O∵ △ABC与△A`B`C`关
于点O成中心对称
∴ △ABC≌ △A`B`C`∵△ABC与△A`B`C`关
于点O成中心对称
∴AA`、BB`、CC`经过点O
且 OA=OA`,OB=OB`,OC=OC`(看图)(再看图) 由已知条件,如果把其中一个图形绕着这个点
旋转180°,它必须与另一个图形重合,根据中心对
称的定义,可知这两个图形关于这一点对称。 逆定理 如果两个图形的对
应点连线都经过某一点,并且被这
一点平分,那么这两个图形关于这
一点对称。 定理2 关于中心对称的两个图形,对称点的连线都经过对称中心,并且被对称中心平分。②结论是什么?②(对称点的连线都经过对称中心,
并且被对称中心平分)③它的逆命题是什么?③(如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。)(2)我们如何证明这个逆命题是正确的?定理2的逆命题作为:①(两个图形成中心对称)现在我们来研究定理2的逆命题,先看定理2。命题的已知条件(看图)命题的结论是两个图形关于这点对称(看图)AOA′ 灵活运用,体会内涵
点的中心对称点的作法AA′B′BO 线段的中心对称线段的作法例题 已知四边形ABCD和点O(如图),画四边形
A`B`C`D`,使它与已知四边形关于点O对称。ABCDO分析:要画四边形ABCD关
于点O的对称图形,只要画
A、B、C、D四点关于点O
的对称点。再顺次连接各点
即可。画法:1。连接AO并延长到A`,使
OA=OA`,得到点A的对称点A`。2。同样画B、C、D的对称点B`、
C`、D`。3。顺次连接A`、B`、C`、D`各点。∴四边形A`B`C`D`就是
所求的四边形。A′B′C ′1. 如图,已知等边△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称.练 习O[例4] 如图,已知△ABC与△A’B’C’中心对称,
求出它们的对称中心O。O[例4] 如图,已知△ABC与△A’B’C’中心对称,
求出它们的对称中心O。判断下列两个图形是否成中心对称(1)(2)(3)(4)想一想:2。判断正误:
(1)轴对称的两个图形一定是全等形,但全等的两个图形
不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是全等形。但全等的两个
图形不一定是成中心对称的图形。 ( )
(3)全等的两个图形,不是成中心对称的图形,就是成轴
对称的图形。 ( ) 3。选择题:
如果两个图形成中心对称,下列说法正确的是 ( )
(1)对称点连线必经过对称中心,且被对称中心平分。
(2)这两个图形一定是全等形。
(3)把一个图形绕着对称中心旋转后定与另一个图形重合。
(A)(1)(2)(3)(B)(2)(3)
(C)(1)(3) (D)(1)(2)D基础练习(一)画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。DABC∴四边形AEFG为(1)所求作。∴四边形BCMN为(2)所求作。提高练习 两个人轮流在桌子上摆放硬币.规则是每人每次摆一个在桌面上,摆好之后不许移动.不允许任何两枚硬币有重叠部分,这样经过多次摆放,规定谁放下最后一枚,并使得对方没有再放的位置,就算是谁获胜。
按照这个规则你用什么方法才能取胜呢?需要智慧的游戏分析:设想桌面很小,仅与硬币同样大小,这时显然是先放者一定获胜。再设想桌面直径仅为硬币直径的2倍,这时,先放者为了获胜,肯定不会将硬币放的挨上圆桌边缘,只要他让硬币压上桌面中心,就使对方无法再放了。看来,桌面中心是个举足轻重的位置,值得认真对待,对于一般圆桌,设想甲先置一枚硬币于圆桌中心,待乙方置一枚硬币于桌面上A处后,甲再往A处,A处关于中心的对称位置放置一枚,这样轮流下去,只要乙有位置放,甲就也有。
解:先放者获胜,操作办法是,第一枚硬币要放在桌面中心处,然后每次都往对方所放位置关于
桌面中心的对称处放。 你要争取先放,并把第1枚硬币放在桌面的对称中心上,以后你应该根据对方所放硬币的位置,在它关于中心对称的位置上放下一枚同样大小硬币.这样,由于对称性,只要对方能放得下一枚硬币,你就保证能在其对称位置上放下一枚同样大小的硬币,因此,失败绝对轮不到你. 分析:
同课章节目录
